Lógica NOR
La lógica NOR hace referencia al hecho de que, debido a que la función NOR tiene una funcionalidad completa, al igual que ocurre con la puerta NAND, todos los sistemas lógicos se pueden convertir en puertas NOR. En principio, cualquier función lógica combinatoria puede realizarse con suficientes puertas NOR.

El primer sistema embebido, el Apollo Guidance Computer, se construyó exclusivamente a partir de puertas NOR, aproximadamente 5,600 en total para las últimas versiones. Hoy en día, los circuitos integrados no se construyen exclusivamente a partir de un solo tipo de puerta. En su lugar, se utilizan herramientas de automatización de diseño electrónico para convertir la descripción de un circuito lógico en una netlist de puertas complejas (celdas estándars) o transistores (diseño a medida).
NOR
Una puerta NOR es lógicamente una puerta OR negada. Por sí misma tiene la siguiente tabla de verdad:
 | |||||||||||||||||||||
|
Q = A NOR B
| |||||||||||||||||||||
Creación de otras puertas usando puertas NOR
Una puerta NOR es una puerta universal, lo que significa que cualquier otra puerta se puede representar como una combinación de puertas NOR.[1]
NOT
Esto se hace uniendo las entradas de una puerta NOR. Como una compuerta NOR es equivalente a una compuerta OR unida a una compuerta NOT, esto automáticamente se encarga de la parte "OR" de la compuerta NOR, eliminándola de la consideración y dejando solo la parte NOT.
| Puerta NOT deseada | Construcción con NOR | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
 |  | |||||||||
| Q = NOT( A ) | = A NOR A | |||||||||
| ||||||||||
OR
Una puerta OR se crea negando la salida de una puerta NOR. Tengase en cuenta que, como ya se indicó más arriba, una puerta NOT es equivalente a una puerta NOR con sus entradas unidas.
| Puerta OR deseada | Construcción con NOR | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
 |  | ||||||||||||||||||||
| Q = A OR B | = (A NOR B) NOR (A NOR B) | ||||||||||||||||||||
| |||||||||||||||||||||
AND
Una puerta AND da una salida 1 cuando ambas entradas son 1. Por lo tanto, una compuerta AND se realiza invirtiendo las entradas de una puerta NOR. De nuevo, tenga en cuenta que una puerta NOT es equivalente a una NOR con sus entradas unidas.
| Puerta AND deseada | Construcción con NOR | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
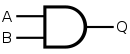 |  | ||||||||||||||||||||
| Q = A AND B | = (A NOR A) NOR (B NOR B) | ||||||||||||||||||||
| |||||||||||||||||||||
NAND
Una puerta NAND se crea invirtiendo la salida de una compuerta AND.
| Puerta NAND deseada | Construcción con NOR | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
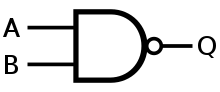 |  | ||||||||||||||||||||
| Q = A NAND B | = [ ( A NOR A ) NOR ( B NOR B ) ] NOR [ ( A NOR A ) NOR ( B NOR B ) ] | ||||||||||||||||||||
| |||||||||||||||||||||
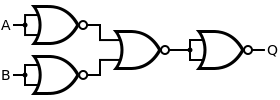
XNOR
Una puerta XNOR se realiza conectando cuatro compuertas NOR como se muestra a continuación. Esta construcción conlleva un retraso de propagación tres veces mayor que el de una sola puerta NOR.
| Puerta XNOR deseada | Construcción con NOR | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
 |  | ||||||||||||||||||||
| Q = A XNOR B | = [ A NOR ( A NOR B ) ] NOR [ B NOR ( A NOR B ) ] | ||||||||||||||||||||
| |||||||||||||||||||||
Alternativamente, se puede invertir la entrada B de la puerta XOR con el retardo de propagación de 3 puertas. Esta construcción utiliza cinco puertas en lugar de cuatro.
| Puerta deseada | Construcción con NOR |
|---|---|
 |  |
| Q = A XNOR B | = [ B NOR ( A NOR A ) ] NOR [ A NOR ( B NOR B ) ] |
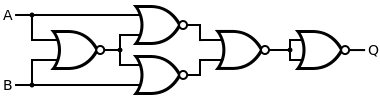
XOR
Una compuerta XOR se puede realizar conectando la salida de 3 compuertas NOR (conectadas como una compuerta AND) y la salida de una compuerta NOR a las entradas respectivas de una compuerta NOR. Esta construcción conlleva un retraso de propagación tres veces mayor que el de una sola puerta NOR y usa cinco puertas.
| Puerta XOR deseada | Construcción con NOR | ||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
 |  | ||||||||||||||||||||
| Q = A XOR B | = [ ( A NOR A ) NOR ( B NOR B ) ] NOR ( A NOR B ) | ||||||||||||||||||||
| |||||||||||||||||||||
Alternativamente, la versión de 4 compuertas de la compuerta XNOR se puede usar con un negador. Esta construcción tiene un retardo de propagación cuatro veces (en lugar de tres veces) el de una sola puerta NOR.
| Puerta deseada | Construcción con NOR |
|---|---|
 |  |
| Q = A XOR B | = { [ A NOR ( A NOR B ) ] NOR [ B NOR ( A NOR B ) ] } NOR { [ A NOR ( A NOR B ) ] NOR [ B NOR ( A NOR B ) ] } |
Véase también
Referencias
- Sistemas Digitales. Tema 5: Análisis de la lógica combinacional Archivado el 7 de mayo de 2019 en Wayback Machine. - Vargas, Héctor. Pontificia Universidad Católica de Valparaíso