Método de Chapman-Enskog
Al finalizar el siglo XIX se conoce la ecuación de Boltzmann que rige la dinámica del medio gaseoso a la escala microscópica y las ecuaciones de Euler y de Navier-Stokes para el nivel macroscópico. Pasar de una escala a la otra constituye una parte del sexto problema de Hilbert. David Hilbert, autor de las declaraciones de los principales problemas considerados al finalizar el siglo XIX plantea las bases de un método bajo la forma de un desarrollo que lleva su nombre (1912). Hará falta esperar algunos años para que Sydney Chapman y David Enskog propongan simultáneamente e independientemente en 1916 y 1917 una solución a este problema.[1][2][3] Más recientemente este método se ha extendido al caso de un gas en desequilibrio termodinámico,[4] siendo este último aspecto un área de investigación muy activa en la actualidad.
El método de Chapman-Enskog es un método de perturbaciones que consiste en definir la solución bajo la forma de series de funciones de distribución en función de un "pequeño parámetro" asimilable al número de Knudsen. En orden cero se encuentra la distribución de Maxwell-Boltzmann y las ecuaciones de Euler. El orden uno permite conocer la expresión de los flujos de calor y de cantidad de movimiento y aquella de los coeficientes de transporte (los coeficientes de difusión por gradientes de concentración, de presión y de temperatura, las viscosidades dinámica, volumétricas, y la conductividad). De los potenciales de interacción molecular. Este enfoque permite encontrar las ecuaciones de Navier-Stokes y para justificar la difusión por gradientes térmico, desconocida en el tiempo en el que están publicados los trabajos de Chapman y de Enskog. Este método permite calcular todos estos coeficientes a partir del conocimiento de uno de ellos mediante la reconstitución a una medida (generalmente la viscosidad) de un potencial de interacción como el potencial de Lennard-Jones.
Harold Grad ha propuesto un enfoque alternativo que consiste en buscar la solución por los métodos de momentos de la función de distribución (1949). La ecuación de Boltzmann está multiplicada por ( es la velocidad microscópica de la ecuación de Boltzmann y el producto tensorial, e integrado en velocidad. En este tipo de método, el término n de la expansión queda en función del término (n+1), por lo que debemos hacer una hipótesis para "cerrar" el sistema. Grad asume la solución expresada por una serie truncada de polinomios de Hermite. David Levermore ha propuesto más recientemente (1996) un cierre que usa una propiedad general: la solución maximiza la entropía del sistema de fermiones que son las partículas del medio que él estudió.[5] De los códigos de cálculo basado en estos métodos están quedado en la propiedad del laboratorio porque no aportando una ganancia notable en términos de propiedad de validez (en términos de número de Knudsen) por informe a los códigos estándares que resuelven las ecuaciones de Navier-Stokes, los cuales han hecho el objeto de desarrollos considerables.
Ecuaciones de evolución microscópica y macroscópica
Nivel microscópico
Apuntamos la función de distribución, estadística de la velocidad. . en el momento en el punto para la partícula (átomo o molécula) perteneciente a la especie . El número probable de partículas en el volumen velocidades en este momento es . La distribución estadística , por lo tanto se mide en s3⋅m-6.
La ecuación de Boltzmann se escribe como
dónde , es el operador (o núcleo) de colisión, es un operador integral cuadrático que se describe a continuación, dando el efecto de las colisiones que se supondrán elásticas para simplificar el problema: no hay intercambio entre los grados de libertad interna y traslación, no hay reacción química. Por lo tanto se excluye el volumen de viscosidad que resulta de este tipo de intercambio.
Hay tantas distribuciones como de especies presentes en el medio. A cada una corresponde una ecuación de Boltzmann acoplada a las demás por los segundos miembros que representan colisiones homogéneas () o heterogéneas ().
El choque elástico
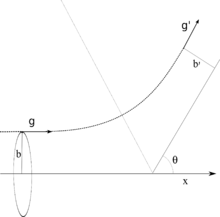
Las velocidades antes de la interacción en un Sistema de referencia inercial son y . Los índices representan indistintamente una misma especie o dos especies diferentes. Las velocidades después de la interacción son y . Después nos colocamos en un sistema centrado en el centro de gravedad, que tiene una velocidad constante a causa de la conservación de la cantidad de movimiento. En este sistema que es por lo tanto galileano, la velocidad inicial de la partícula es la velocidad relativa . Por simetría se puede afirmar que la trayectoria estará contenida en el plano que contiene el origen y . Elegimos un punto de referencia como: (ver figura). En esta referencia, el ángulo de desviación respecto al eje es . Definimos también el parámetro de impacto de la velocidad relativa y el potencial de interacción que, se supone, depende sólo de la distancia de las dos partículas que interaccionan. Si esta hipótesis es rigurosa para la interacción entre dos átomos, se puede considerar utilizable también para dos moléculas. El potencial es entonces un potencial medio estadístico.
La dirección de salida de interacción está definida por: . Las velocidades finales se pueden calcular a partir de las siguientes consideraciones:
- la conservación de la cantidad de movimiento en la interacción implica
- la velocidad relativa tiene un módulo constante debido a la conservación de la energía, por lo que o
Las velocidades después de la interacción son por lo tanto:
Además la conservación de momento cinético durante la interacción conduce a .
El sistema que describe la colisión es reversible. El Teorema de Liouville (mecánica hamiltoniana) permite escribir
La colisión del núcleo
El número probable de partículas que atraviesan el área por unidad de tiempo es . Estas partículas interactúan con el número probable de partículas en el volumen elemental. . El número de partículas que desaparecen de la estadística por unidad de tiempo es con
- .
De la misma manera, contamos la cantidad de partículas que aparecen por unidad de tiempo, tenemos
- .
Dadas las relaciones anteriores para la colisión, el operador de colisión se escribe
- ,
donde y dependen explícitamente de las velocidades de colisión iniciales y . Esta ecuación está nombrada como la ecuación de Wang Chang y Uhlenbeck.
Se puede dar una formulación equivalente que introduce la sección transversal diferencial y se define:
por lo tanto
Las variables
La ecuación de Boltzmann describe la evolución de partículas a nivel macroscópico. Para describir cada una de las especies a nivel macroscópico esto se define:
| - Densidad de partículas | ||
| - Densidad | ||
| - Velocidad media | ||
| - Energía interna | ||
Podemos entonces definir valores para el conjunto de las especies
| - Velocidad total | (velocidad baricéntrica de todas las partículas) | |
| - Velocidad de difusión | (cantidad cinématique) |
Algunas variables auxiliares ( es el número de Avogadro)
| - Fracción de volumen | tal que | |
| - Fracción de masa | tal que | |
| - Masa molar | de valor medio |
Los flujos
El flujo de cantidad es por definición la cantidad donde
esto se define observando el producto producto diádico
| - Flujo de masa | ||
| - Tensor de presiones | que representa el flujo de cantidad de movimiento. Es simétrico por construcción. | |
| - Presión parcial | se define a partir de la traza del tensor de presiones. | |
| - Flujo de calor | representa el flujo de energía interna. |
Los flujos globales se obtienen simplemente sumando así como la presión: .
Podemos entonces definir una temperatura a partir de la ecuación de estado
Ecuaciones de evolución
Multiplicando cada una de las ecuaciones de Boltzmann sucesivamente por cada uno de los invariantes de colisión , integrando en las velocidades y, si es necesario, en la especie, se obtienen las ecuaciones de evolución macroscópicas llamadas ecuaciones de producto contraído.
Todos los segundos miembros son nulos a causa de las leyes de conservación
Así obtenemos un sistema de evolución , y en el que los flujos , y quedan por definir.
Ecuación de Boltzmann adimensional
Se supone que es un medio homogéneo (una sola especie presente).
Con el fin de estimar la aportación de cada término en la ecuación de Boltzmann es necesario modificar este. Para eso se define las cantidades de referencia siguiente:
- la temperatura de la cual deducimos una velocidad de referencia que es la velocidad del sonido para una gas perfecto
- la longitud de referencia macroscópica Relacionado con el problema que se define un tiempo de referencia Relacionados con la propagación de ondas acústicas
- presión de referencia , con la que se define una densidad de referencia y la cantidad
- una velocidad de referencia microscópica que corresponde a la velocidad mediana de una partícula
- otra velocidad de referencia microscópica que corresponde a la velocidad relativa promedia entre dos partículas
- una longitud de referencia microscópica correspondiente a la trayectoria libre promedia donde es la sección transversal diferencial.
Si ahora definimos las variables reducidas , , , , y , la ecuación de Boltzmann esta escrita
donde:
- número de Strouhal que mide la variación temporal del sistema,
- número de Knudsen cuyo inverso es el término de colisión, por lo que nos da la tendencia a volver al equilibrio. En la práctica, para que las ecuaciones del continuo sean válidas, es necesario que , típicamente.
Formulación de la solución
Escribimos la solución como una serie usando un parámetro del mismo orden de magnitud que el número de Knudsen
Como verifica las leyes de conservación de los invariantes de colisión , cada uno de los términos de desarrollo también deben de verificarlas. De donde se imponen las siguientes restricciones sobre la solución.
- .
Por último, insertamos esta aproximación en la ecuación de Boltzmann, y separamos los términos correspondientes a cada potencia de para estudiar los distintos órdenes.
Al orden cero
Se obtiene simplemente
Esta ecuación está verificada si todos los términos que la componen son nulos, así que en particular
Lo que implica
o
Es un variante colisional. Por lo tanto se escribe como una combinación lineal de las invariantes colisionales canónicos
Introduciendo esta expresión en las ecuaciones que definen las variables microscópicas se identifica los parámetros de este desarrollo y se encuentra la ley de distribución de las velocidades de Maxwell
con. . Los flujos de difusión se anulan, así como el flujo de calor . El tensor de presión está reducido a su traza donde es la matriz unidad. Las ecuaciones macroscópicas correspondientes son las ecuaciones de Euler.
Al orden uno
A orden uno, se obtiene una ecuación integral de Fredholm para la incógnita
La difícil resolución de esta ecuación permite dar las diversas cantidades desconocidas de las ecuaciones de Enskog que se puede entonces asimilar a las ecuaciones de Navier-Stokes.
El flujo de difusión
Se obtiene bajo forma de un sistema lineal denominado sistema de Stefan-Maxwell
Donde vemos la aparición coeficiente de difusión binaria y el "coeficiente de difusión térmica multicomponente", (en realidad un número adimensional) (que no son coeficientes de difusión y que pueden ser negativos) por:
Para un medio con especies el rango de este sistema es ya que . Su solución
Encontramos los términos de difusión por gradiente de concentración, de presión y de temperatura (efecto Soret). es el coeficiente de difusión multicomponente, solución de un sistema lineal que involucra los coeficientes binarios. Este sistema también es de rango términos La solución no es única e implica términos independientes. Generalmente elegimos por simetría, pero esta elección es arbitraria.
Hay diversas soluciones aproximadas del sistema de Stefan-Maxwell que permite obtener una expresión explícita del flujo de difusión bajo una forma semejante a la ley de Fick, la cual no es exacta para una mezcla binaria.
El tensor de presiones
El tensor de presiones tiene una forma clásica
donde es el tensor unitario El tensor de estrés viscoso
Un término adicional aparece en la presión cuando se tienen en cuenta las interacciones inelásticas. Su influencia es débil incluso totalmente despreciable para los gases poco densos.[4]
Se observa que la hipótesis de Stokes se justifica naturalmente por este enfoque.
El flujo de calor
Está dado por
Esta es la conductividad térmica. El último término de la ecuación es el corolario del efecto Soret y está nombrado efecto Dufour.
Los coeficientes de transporte
Los coeficientes de transporte se expresan en forma de sistemas lineales que involucran cantidades del tipo , las cuales se desarrollan en polinomios de Sonine-Laguerre. Los coeficientes del desarrollo se expresan en funciones integrales de colisión. En la práctica, estamos satisfechos con el primer orden para el desarrollo y las integrales de colisión son funciones de la temperatura tabuladas por varios autores. Además hay soluciones aproximadas de los sistemas lineales que dan los diversos coeficientes bajo forma explícita.
La función de distribución
La función de distribución es
donde se da en el flujo de difusión
Esta función de distribución es necesaria para el cálculo de la capa de Knudsen que da las condiciones a la pared para la ecuación de Navier-Stokes.
Al orden dos
Aquí nuevamente obtenemos una integral de Fredholm para la incógnita
David Burnett propuso en 1935 una solución de esta ecuación. Esta tiene el inconveniente de no respetar el théorème[6] H. Parece que la subida en orden constituye un callejón sin salida, todas las variantes propuestas hasta este día no resuelven este problema.[7]
Referencias
- (en) Sydney Chapman et Thomas George Cowling, The Mathematical Theory of Non-uniform Gases, Cambridge University Press, (ISBN 0-521-40844-X)
- (en) Joseph Oakland Hirschfelder, Charles Francis Curtiss et Robert Byron Bird, Molecular Theory of Gases and Liquids, John Wiley and Sons, (ISBN 978-0-471-40065-3)
- (en) Gilberto Medeiros Kremer, « The Methods of Chapman-Enskog and Grad and Applications », RTO-EN-AVT 194, 2011
- Raymond Brun, Introduction à la dynamique des gaz réactifs, Cépaduès, (ISBN 978-2-364-93190-9)
- (en) Charles David Levermore, « Moment Closure Hierarchies for Kinetic Theories », Journal of Statistical Physics, vol. 83, (lire en ligne)
- Byung Chan Eu, Nonequilibrium Statistical Mechanics. Ensemble Method., Springer, (ISBN 978-90-481-5007-6)
- Cédric Villani, Limites hydrodynamiques de l'équation de Boltzmann, coll. « Séminaire Bourbaki » (no 893 ),