Método de la viga conjugada

El método de la viga conjugada es un método de análisis estructural para determinar pendientes y deflexiones de una viga. Fue desarrollado por Christian O. Mohr. En esencia, requiere la misma cantidad de cálculo que los teoremas del momento de área para determinar la pendiente de una viga o su deflexión; aun así, este método aplica solo los principios de la estática, por lo que su aplicación puede resultar más familiar.[1] La viga conjugada se define como una viga imaginaria con las mismas dimensiones (longitud) que la viga original, pero una carga en cualquier punto de la viga conjugada es igual al momento flector en ese punto de la viga original dividido por EI.[2]

(0) Viga real, (1) cortante y momento, (2) viga conjugada, (3) pendiente y deflexión

La base para el método proviene la semejanza de las ecuaciones 1 y 2 con las 3 y 4. Para mostrar esta semejanza, estas ecuaciones se muestran debajo.

$Ec.\,1)\;{\frac {dV}{dx}}=w$	$Ec.\,3)\;{\frac {d^{2}M}{dx^{2}}}=w$
$Ec.\,2)\;{\frac {d\theta }{dx}}={\frac {M}{EI}}$	$Ec.\,4)\;{\frac {d^{2}v}{dx^{2}}}={\frac {M}{EI}}$

Integrando, las ecuaciones quedan de esta forma:

$V=\int w\,dx$	$M=\int \int w\,dxdx$
$\theta =\int \left({\frac {M}{EI}}\right)dx$	$v=\int \left[\int \left({\frac {M}{EI}}\right)dx\right]dx$

Aquí el cortante V se compara con la pendiente θ, el momento M se compara con la deflexión v, y la carga externa w compara con el diagrama M/EI. En la figura se muestra un diagrama de cortante, momento y otro diagrama de deflexión. El diagrama M/EI es un diagrama de momento dividido por el producto del módulo de Young de la viga y su momento de inercia.

Para hacer uso de esta comparación ahora consideraremos una viga que tiene la misma longitud que la viga real, pero llamada aquí como la «viga conjugada». La viga conjugada está "cargada" con el diagrama M/EI derivado de la carga en la viga real. Con estas comparaciones, podemos declarar dos teoremas relacionados con la viga conjugada:

Teorema 1: La pendiente en un punto en la viga real es numéricamente igual al valor del cortante en el punto correspondiente de la viga conjugada.
Teorema 2: La deflexión de un punto en la viga real es numéricamente igual al valor del momento en el punto correspondiente de la viga conjugada.

Apoyos en la viga conjugada

Al dibujar la viga conjugada, es importante que el cortante y el momento desarrollado en los apoyos de la viga conjugada consideren la pendiente y la deflexión de la viga real en sus apoyos, como consecuencia de los teoremas 1 y 2. Por ejemplo, como se muestra debajo, en una articulación o un rodillo en un extremo de la viga real no hay deflexión, pero sí hay una pendiente. Por consiguiente, a partir de los teoremas 1 y 2, la viga conjugada debe estar apoyada en una articulación o un rodillo, pues estos apoyos no tienen momento pero sí un cortante o reacción. Cuando la viga real está empotrada, tanto la pendiente como la deflexión son cero. La viga conjugada correspondiente tiene un extremo libre en este punto, pues allí tanto el momento como el cortante son cero. En las tablas debajo, se muestran los apoyos correspondientes a una viga conjugada a partir de los de una viga real. Se hace notar que, como regla general, despreciando las fuerzas axiales, las vigas isostáticas tienen vigas conjugadas isostáticas, mientras que las vigas hiperestáticas tienen vigas conjugadas inestables. Aunque ocurra esto, la carga de M/EI provee el "equilibrio" necesario para que la viga conjugada sea estable.[1]

Apoyos en la viga real vs apoyos en la viga conjugada[3]
Viga real		Viga conjugada
Empotramiento		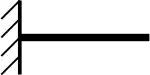Extremo libre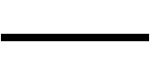
$v=0$ $\theta =0$		${\overline {M}}=0$ ${\overline {Q}}=0$
Extremo libre		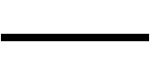Empotramiento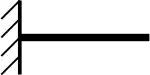
$v\not =0$ $\theta \not =0$		${\overline {M}}\not =0$ ${\overline {Q}}\not =0$
Apoyo articulado		Apoyo articulado
$v=0$ $\theta \not =0$		${\overline {M}}=0$ ${\overline {Q}}\not =0$
Articulación o rodillo interno		Articulación interna o bisagra
$v=0$ ${\displaystyle \theta$ continua		${\overline {M}}=0$ ${\overline {Q}}:$ continuo
Articulación interna o bisagra		Articulación o rodillo interno
$v:$ continua ${\displaystyle \theta$ discontinua		${\overline {M}}:$ continuo ${\overline {Q}}:$ discontinuo

Ejemplos de vigas conjugadas
Viga real		Viga conjugada
Viga sencilla
Viga en voladizo
Viga con vuelo en el lado izquierdo
Viga con vuelos en ambos lados
Viga Gerber (2 segmentos)
Viga Gerber (3 segmentos)

Procedimiento de análisis

El siguiente procedimiento provee un método que puede ser utilizado para determinar la pendiente y la deflexión en un punto de la curva elástica usando el método de la viga conjugada.

Viga conjugada

Dibuje la viga conjugada correspondiente a la viga real. Esta viga tiene la misma longitud que la viga original y sus apoyos se corresponden con la tabla de arriba.
En general, si el apoyo real permite una pendiente, el apoyo de la viga conjugada debe desarrollar un cortante, y si el apoyo de la viga real permite desplazamiento, el apoyo de la viga conjugada debe desarrollar un momento.
Se carga la viga conjugada con el diagrama M/EI de la viga real. Esta carga se asume distribuida a lo largo de la viga conjugada y su sentido es hacia arriba cuando M/EI es positivo y hacia abajo cuando M/EI es negativo. En otras palabras, la carga siempre actúa en un sentido hacia afuera de la viga.[1]

Equilibrio

Utilizando las ecuaciones de la estática, determine las reacciones en los apoyos de la viga conjugada.
Realice un corte en la viga conjugada en el punto donde la pendiente θ y la deflexión Δ de la viga real se van a determinar. En la sección, calcule el cortante V y el momento M y estos valores serán iguales a θ y Δ, respectivamente.[1]

Véase también

Referencias

Structural Analysis. Upper Saddle River, NJ: Pearson. 2009. pp. 328-335.
Strength of materials. Consultado el 20 de noviembre de 2014.
Okmamura (1988)、p.171。

Datos: Q5161152

Este artículo ha sido escrito por Wikipedia. El texto está disponible bajo la licencia Creative Commons - Atribución - CompartirIgual. Pueden aplicarse cláusulas adicionales a los archivos multimedia.

[Hibbeler_2009_328–335-1] Structural Analysis. Upper Saddle River, NJ: Pearson. 2009. pp. 328-335.

[2] Strength of materials. Consultado el 20 de noviembre de 2014.

[okamura_171-3] Okmamura (1988)、p.171。