Método del conjunto de nivel

El método del conjunto de nivel es una técnica numérica para delinear interfaces y formas. La ventaja del método del conjunto de nivel es que se puede realizar cálculos numéricos que involucran curvas y superficies sobre una cuadrícula cartesiana fija sin tener que parametrizar estos objetos (esto se llama el enfoque euleriano).[1] Además, el método del conjunto de nivel hace que sea muy fácil seguir las formas que cambian de topología, por ejemplo, cuando una forma se divide en dos, crea agujeros o la inversa de estas operaciones. Todo esto hace que este método sea una gran herramienta para el modelado de objetos que cambian en el tiempo, como el inflado de un airbag o una gota de aceite flotando en el agua.

Descripción

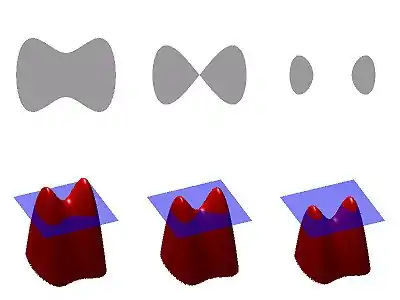
Una ilustración del método del conjunto de nivel

Una manera muy simple pero poderosa para comprender el método del conjunto de nivel es estudiar la ilustración adjunta antes de proceder a una definición más técnica, la que entonces se hace más comprensible. La figura de la derecha ilustra varias ideas importantes sobre el método del conjunto de nivel. En la esquina superior izquierda vemos una forma, es decir, una región delimitada, con un límite de buen comportamiento. Debajo de ella, la superficie roja es la gráfica de una función de conjunto de nivel de $\varphi$ que determina esta forma, y la región azul representa el plano $x-y$ . El límite de la forma es entonces el conjunto de nivel cero de $\varphi$ , mientras que la forma en sí es el conjunto de puntos en el plano para el cual $\varphi$ es positivo (interior de la forma) o cero (en el borde).

Véase también

Segmentación (procesamiento de imágenes)#Método del conjunto de nivel

Referencias

Osher, S.; Sethian, J. A. (1988), «Fronts propagating with curvature-dependent speed: Algorithms based on Hamilton-Jacobi formulations», J. Comput. Phys. 79: 12-49..

Datos: Q1751397

Este artículo ha sido escrito por Wikipedia. El texto está disponible bajo la licencia Creative Commons - Atribución - CompartirIgual. Pueden aplicarse cláusulas adicionales a los archivos multimedia.

[1] Osher, S.; Sethian, J. A. (1988), «Fronts propagating with curvature-dependent speed: Algorithms based on Hamilton-Jacobi formulations», J. Comput. Phys. 79: 12-49..