Astrodinámica
La astrodinámica o mecánica orbital es la aplicación de la balística y la mecánica celeste a los problemas prácticos relativos al movimiento de cohetes y otras naves espaciales. El movimiento de estos objetos se calcula generalmente a partir de las leyes de Newton del movimiento y de la gravitación universal. Es una disciplina central dentro del diseño y control de misiones espaciales.

La mecánica celestial trata más ampliamente la dinámica orbital de los sistemas bajo la influencia de la gravedad, incluyendo tanto las naves espaciales como los cuerpos astronómicos naturales tales como sistemas estelares, planetas, lunas y cometas. La mecánica orbital se centra en las trayectorias de las naves espaciales, incluidas las maniobras orbitales, los cambios en el plano de la órbita y las transferencias interplanetarias, y es utilizada por los planificadores de misiones para predecir los resultados de las maniobras propulsivas. La relatividad general es una teoría más exacta que las leyes de Newton para calcular órbitas, y a veces es necesaria para una mayor precisión o en situaciones de alta gravedad (como órbitas cercanas al Sol). Es la parte de la astronomía que estudia las órbitas, especialmente de los satélites artificiales y sondas espaciales.
El movimiento de los planetas y otros cuerpos naturales es dominio de la mecánica celeste, disciplina que consiste en la aplicación de las leyes de Newton del movimiento y de la ley de la gravitación universal.
Historia
Hasta el auge de los viajes espaciales en el siglo XX, apenas se distinguía entre mecánica orbital y celeste. En la época del Sputnik, el campo se denominaba "dinámica espacial".[1] Las técnicas fundamentales, como las utilizadas para resolver el problema kepleriano (determinar la posición en función del tiempo), son por tanto las mismas en ambos campos. Además, la historia de los campos es compartida casi en su totalidad.
Johannes Kepler fue el primero en modelizar con éxito las órbitas planetarias con un alto grado de precisión, publicando sus leyes en 1605. Isaac Newton publicó leyes más generales del movimiento celeste en la primera edición de Philosophiæ Naturalis Principia Mathematica (1687), que ofrecía un método para hallar la órbita de un cuerpo que sigue una trayectoria parabólica a partir de tres observaciones.[2] Este método fue utilizado por Edmund Halley para establecer las órbitas de varios cometas, incluido el que lleva su nombre. El método de aproximación sucesiva de Newton fue formalizado en un método analítico por Leonhard Euler en 1744, cuyo trabajo fue a su vez generalizado a órbitas elípticas e hiperbólicas por Johann Lambert en 1761-1777.
Otro hito en la determinación de órbitas fue la ayuda de Carl Friedrich Gauss en la "recuperación" del planeta enano Ceres en 1801. El método de Gauss fue capaz de utilizar sólo tres observaciones (en forma de pares de ascensión recta y declinación), para encontrar los seis elementos orbitales que describen completamente una órbita. La teoría de la determinación de órbitas se ha desarrollado posteriormente hasta el punto de que hoy en día se aplica en los receptores GPS, así como en el seguimiento y catalogación de planetas menores recién observados. La moderna determinación y predicción de órbitas se utiliza para operar todo tipo de satélites y sondas espaciales, ya que| es necesario conocer sus posiciones futuras con un alto grado de precisión.
La Astrodinámica fue desarrollada por el astrónomo Samuel Herrick a partir de la década de 1930. Consultó al científico de cohetes Robert Goddard y le animó a continuar su trabajo sobre técnicas de navegación espacial, ya que Goddard creía que serían necesarias en el futuro. En la década de 1960, las técnicas numéricas de astrodinámica se combinaron con nuevos y potentes ordenadores, y los seres humanos estuvieron listos para viajar a la Luna y regresar.
Técnicas prácticas
Reglas empíricas
Las siguientes reglas empíricas son útiles para situaciones aproximadas por la mecánica clásica bajo los supuestos estándar de la astrodinámica que se describen a continuación. El ejemplo concreto que se expone es el de un satélite orbitando alrededor de un planeta, pero las reglas empíricas también podrían aplicarse a otras situaciones, como las órbitas de cuerpos pequeños alrededor de una estrella como el Sol.
- Leyes de Kepler:
- Las órbitas son elípticas, con el cuerpo más pesado en un foco de la elipse. Un caso especial de esto es una órbita circular (un círculo es un caso especial de elipse) con el planeta en el centro.
- Una línea trazada desde el planeta hasta el satélite barre áreas iguales en tiempos iguales independientemente de la porción de la órbita que se mida.
- El cuadrado del período orbital de un satélite es proporcional al cubo de su distancia media al planeta.
- Sin aplicar fuerza (como encender el motor de un cohete), el periodo y la forma de la órbita del satélite no cambiarán.
- Un satélite en una órbita baja (o una parte baja de una órbita elíptica) se mueve más rápidamente con respecto a la superficie del planeta que un satélite en una órbita más alta (o una parte alta de una órbita elíptica), debido a la mayor atracción gravitatoria cerca del planeta.
- Si se aplica empuje en un solo punto de la órbita del satélite, éste volverá a ese mismo punto en cada órbita posterior, aunque el resto de su trayectoria cambiará. Por tanto, no se puede pasar de una órbita circular a otra con una sola aplicación breve de empuje.
- Desde una órbita circular, el empuje aplicado en dirección opuesta al movimiento del satélite cambia la órbita a una elíptica; el satélite descenderá y alcanzará el punto orbital más bajo (el periapse) a 180 grados de distancia del punto de disparo; después volverá a ascender. El período de la órbita resultante será menor que el de la órbita circular original. El empuje aplicado en la dirección del movimiento del satélite crea una órbita elíptica con su punto más alto (ápside) a 180 grados de distancia del punto de disparo. El periodo de la órbita resultante será mayor que el de la órbita circular original.
Las consecuencias de las reglas de la mecánica orbital son a veces contraintuitivas. Por ejemplo, si dos naves espaciales están en la misma órbita circular y desean acoplarse, a menos que estén muy cerca, la nave que va detrás no puede simplemente encender sus motores para ir más rápido. Esto cambiaría la forma de su órbita, haciendo que ganara altitud y, de hecho, se ralentizara con respecto a la nave líder, perdiendo el objetivo. El encuentro espacial antes del acoplamiento normalmente requiere múltiples encendidos de motores calculados con precisión en múltiples periodos orbitales, necesitando horas o incluso días para completarse.
En la medida en que no se cumplan los supuestos estándar de la astrodinámica, las trayectorias reales variarán de las calculadas. Por ejemplo, la simple resistencia atmosférica es otro factor que complica la trayectoria de los objetos en órbita terrestre baja.
Estas reglas empíricas son claramente inexactas cuando se describen dos o más cuerpos de masa similar, como un sistema estelar binario (véase problema de los n-cuerpos). La mecánica celeste utiliza reglas más generales aplicables a una mayor variedad de situaciones. Las leyes de Kepler del movimiento planetario, que pueden derivarse matemáticamente de las leyes de Newton, sólo son válidas estrictamente para describir el movimiento de dos cuerpos gravitatorios en ausencia de fuerzas no gravitatorias; también describen trayectorias parabólicas e hiperbólicas. En la proximidad de objetos grandes, como las estrellas, las diferencias entre la mecánica clásica y la relatividad general también adquieren importancia.
Velocidad de escape
La fórmula para una velocidad de escape se deriva de la siguiente manera. La energía específica (energía por unidad de masa) de cualquier vehículo espacial está formada por dos componentes, la energía potencial específica y la energía cinética específica. La energía potencial específica asociada a un planeta de masa M viene dada por
donde G es la constante de gravitación universal y r es la distancia entre los dos cuerpos;
mientras que la energía cinética específica de un objeto viene dada por
donde v es su velocidad;
y así la energía orbital específica total es
Puesto que la energía se conserva, no puede depender de la distancia, , desde el centro del cuerpo central al vehículo espacial en cuestión, es decir, v debe variar con r para mantener constante la energía orbital específica. Por lo tanto, el objeto puede alcanzar el infinito sólo si esta cantidad es no negativa, lo que implica
La velocidad de escape desde la superficie de la Tierra es de unos 11 km/s, pero eso es insuficiente para enviar el cuerpo a una distancia infinita debido a la atracción gravitatoria del Sol. Para escapar del Sistema Solar desde un lugar situado a una distancia del Sol igual a la distancia Sol-Tierra, pero no cerca de la Tierra, se requiere una velocidad de unos 42 km/s, pero habrá "crédito parcial" para la velocidad orbital de la Tierra para las naves espaciales lanzadas desde la Tierra, si su aceleración posterior (debida al sistema de propulsión) las lleva en la misma dirección que la Tierra recorre en su órbita.
Fórmulas para órbitas libres
Las órbitas son secciones cónicas, por lo que la fórmula de la distancia de un cuerpo para un ángulo dado corresponde a la fórmula de esa curva en coordenadas polares, que es:
se denomina Parámetro gravitacional estándar. y son las masas de los objetos 1 y 2, y es el momento angular específico del objeto 2 con respecto al objeto 1. El parámetro se conoce como la anomalía verdadera, es la semi-latus rectum, mientras que es la excentricidad orbital, todo ello obtenible a partir de las diversas formas de los seis elementos orbitales independientes.
Órbitas circulares
Todas las órbitas limitadas en las que domina la gravedad de un cuerpo central son de naturaleza elíptica. Un caso especial es la órbita circular, que es una elipse de excentricidad cero. La fórmula para la velocidad de un cuerpo en una órbita circular a una distancia r del centro de gravedad de la masa M puede deducirse como sigue:
La aceleración centrífuga coincide con la aceleración debida a la gravedad.
Entonces
por lo tanto,
donde es la constante de gravitación universal, igual a
- 6.6743 × 10−11 m3/(kg·s2)
Para utilizar correctamente esta fórmula, las unidades deben ser coherentes; por ejemplo, debe estar en kilogramos, y debe estar en metros. La respuesta será en metros por segundo.
La cantidad suele denominarse parámetro gravitacional estándar, que tiene un valor diferente para cada planeta o luna del Sistema Solar.
Una vez conocida la velocidad orbital circular, la velocidad de escape se halla fácilmente multiplicando por
:
Para escapar de la gravedad, la energía cinética debe ser al menos igual a la energía potencial negativa. Por lo tanto,
Órbitas elípticas
Si , entonces el denominador de la ecuación de las órbitas libres varía con la anomalía verdadera , pero permanece positivo, sin llegar nunca a ser cero. Por tanto, el vector de posición relativa permanece acotado, teniendo su menor magnitud en la periapsis , que viene dada por:
El valor máximo de se alcanza cuando . Este punto se denomina apoapsis, y su coordenada radial, denotada , es
Sea la distancia medida a lo largo de la línea absidal desde la periapsis hasta la apoapsis , como se ilustra en la ecuación siguiente:
Sustituyendo las ecuaciones anteriores, obtenemos:
a es el semieje mayor de la elipse. Resolviendo para , y sustituyendo el resultado en la fórmula de la curva de sección cónica anterior, obtenemos:
Período orbital
Bajo supuestos estándar, el período orbital () de un cuerpo que viaja a lo largo de una órbita elíptica puede calcularse como:
donde:
- es parámetro gravitacional estándar,
- la longitud del semieje mayor.
Conclusiones:
- El periodo orbital es igual al de una órbita circular con el radio de la órbita igual al semieje mayor (),
- Para un semieje mayor dado el periodo orbital no depende de la excentricidad (véase también: Tercera ley de Kepler).
Velocidad
Bajo suposiciones estándar la velocidad orbital () de un cuerpo que viaja a lo largo de una órbita elíptica puede calcularse a partir de la ecuación Vis-viva como:
donde:
- es el parámetro gravitacional estándar,
- es la distancia entre los cuerpos en órbita.
- es la longitud del semieje mayor.
La ecuación de velocidad para una trayectoria hiperbólica es:
.
Energía
Bajo supuestos estándar, la energía orbital específica () de la órbita elíptica es negativa y la ecuación de conservación de la energía orbital (la ecuación Vis-viva) para esta órbita puede tomar la forma:
donde:
- es la velocidad del cuerpo orbital y,
- es la distancia del cuerpo en órbita al centro de masa del cuerpo central,
- es el semi-eje mayor,
- es el Parámetro gravitacional estándar.
Conclusiones:
- Para un semieje mayor dado la energía orbital específica es independiente de la excentricidad.
Usando el teorema del virial encontramos:
- la media temporal de la energía potencial específica es igual a .
- la media temporal de es
- la media temporal de la energía cinética específica es igual a
Órbitas parabólicas
Si la excentricidad es igual a 1, entonces la ecuación de la órbita se convierte en:
donde:
- es la distancia radial del cuerpo en órbita desde el centro de masas del cuerpo central,
- es el Momento angular relativo específico del cuerpo en órbita,
- es la anomalía verdadera del cuerpo en órbita,
- es el parámetro gravitacional estándar.
A medida que la anomalía verdadera θ se aproxima a 180°, el denominador se aproxima a cero, de modo que r tiende hacia el infinito. Por lo tanto, la energía de la trayectoria para la que e=1 es cero, y viene dada por:
donde:
- es la velocidad del cuerpo en órbita.
En otras palabras, la velocidad en cualquier lugar de una trayectoria parabólica es:
Órbitas hiperbólicas
Si , la fórmula de la órbita,
describe la geometría de la órbita hiperbólica. El sistema consta de dos curvas simétricas. El cuerpo en órbita ocupa una de ellas; la otra es su imagen matemática vacía. Es evidente que el denominador de la ecuación anterior llega a cero cuando . Denotamos este valor de anomalía verdadera
ya que la distancia radial se aproxima a infinito a medida que la anomalía verdadera se aproxima a , conocida como la anomalía verdadera de la asíntota. Obsérvese que se encuentra entre 90° y 180°. De la identidad trigonométrica se deduce que:
Energía
Bajo supuestos estándar, la energía orbital específica () de una trayectoria hiperbólica es mayor que cero y toma forma la ecuación de conservación de la energía orbital para este tipo de trayectoria:
donde:
- es la velocidad orbital del cuerpo en órbita,
- es la distancia radial del cuerpo orbitante al cuerpo central,
- es el semieje mayor negativo de la órbita de la hipérbola,
- es el parámetro gravitacional estándar.
Velocidad de exceso hiperbólica
Bajo supuestos estándar, el cuerpo que viaja a lo largo de una trayectoria hiperbólica alcanzará en infinito una velocidad orbital llamada exceso de velocidad hiperbólica () que se puede calcular como:
donde:
- es el parámetro gravitacional estándar,
- es el semieje mayor negativo de la hipérbola de la órbita.
El exceso de velocidad hiperbólica se relaciona con la energía orbital específica o energía característica mediante
Cálculo de trayectorias
Ecuación de Kepler
Una aproximación al cálculo de órbitas (principalmente utilizada históricamente) consiste en utilizar la ecuación de Kepler:
- .
donde M es la anomalía media, E es la anomalía excéntrica, y es la centricidad.
Con la fórmula de Kepler, hallar el tiempo de vuelo para alcanzar un ángulo (anomalía verdadera) de desde la periapsis se descompone en dos pasos:
- Calcular la anomalía excéntrica a partir de la anomalía verdadera .
- Calcular el tiempo de vuelo a partir de la anomalía excéntrica .
Encontrar la anomalía excéntrica en un momento dado (el problema inverso) es más difícil. La ecuación de Kepler es trascendental en , lo que significa que no puede resolverse para algebraicamente. La ecuación de Kepler puede resolverse para analíticamente por inversión.
Una solución de la ecuación de Kepler, válida para todos los valores reales de es:
Evaluándolo se tiene:
Alternativamente, la ecuación de Kepler puede resolverse numéricamente. Primero hay que adivinar un valor de y resolver el tiempo de vuelo; luego ajustar según sea necesario para acercar el tiempo de vuelo calculado al valor deseado hasta alcanzar la precisión requerida. Normalmente, se utiliza el método de Newton para lograr una convergencia relativamente rápida.
La principal dificultad de este método es que puede tardar un tiempo prohibitivo en converger para las órbitas elípticas extremas. Para órbitas casi parabólicas, la excentricidad es casi 1, y sustituyendo en la fórmula para la anomalía media, , nos encontramos restando dos valores casi iguales, y la precisión se resiente. Para las órbitas casi circulares, es difícil encontrar la periapsis en primer lugar (y las órbitas verdaderamente circulares no tienen periapsis en absoluto). Además, la ecuación se obtuvo suponiendo una órbita elíptica, por lo que no es válida para órbitas parabólicas o hiperbólicas. Estas dificultades son las que condujeron al desarrollo de la formulación de la variable universal, que se describe a continuación.
Órbitas cónicas
Para procedimientos sencillos, como calcular el delta-v para elipses de transferencia coplanares, los enfoques tradicionales son bastante eficaces. Otras, como la del tiempo de vuelo, son mucho más complicadas, especialmente para órbitas casi circulares e hiperbólicas.
La aproximación cónica parcheada
La órbita de transferencia de Hohmann por sí sola es una mala aproximación para trayectorias interplanetarias porque desprecia la gravedad propia de los planetas. La gravedad planetaria domina el comportamiento de la nave espacial en las proximidades de un planeta y, en la mayoría de los casos, Hohmann sobreestima severamente la delta-v, y produce prescripciones muy inexactas para los tiempos de combustión. Una forma relativamente sencilla de obtener una aproximación de primer orden de delta-v se basa en la técnica de "aproximación cónica parcheada". Hay que elegir el cuerpo gravitatorio dominante en cada región del espacio por la que pasará la trayectoria, y modelar sólo los efectos de ese cuerpo en esa región. Por ejemplo, en una trayectoria de la Tierra a Marte, se empezaría considerando sólo la gravedad de la Tierra hasta que la trayectoria alcanzara una distancia en la que la gravedad de la Tierra dejara de dominar a la del Sol. Se daría a la nave velocidad de escape para enviarla al espacio interplanetario. A continuación, se consideraría únicamente la gravedad del Sol hasta que la trayectoria alcance la vecindad de Marte. Durante esta etapa, el modelo de órbita de transferencia es apropiado. Por último, sólo se considera la gravedad de Marte durante la parte final de la trayectoria, en la que la gravedad de Marte domina el comportamiento de la nave espacial. La nave se aproximaría a Marte en una órbita hiperbólica, y un quemado retrógrado final frenaría la nave lo suficiente como para ser capturada por Marte. Friedrich Zander fue uno de los primeros en aplicar el enfoque patched-conics con fines astrodinámicos, al proponer el uso de la gravedad de cuerpos intermedios para viajes interplanetarios, en lo que hoy se conoce como asistencia gravitatoria.[3]
El tamaño de los "vecindarios" (o esferas de influencia) varía con el radio
donde es el semieje mayor de la órbita del planeta respecto al Sol; y son las masas del planeta y del Sol, respectivamente.
Esta simplificación es suficiente para calcular estimaciones aproximadas de las necesidades de combustible y estimaciones aproximadas del tiempo de vuelo, pero no suele ser lo suficientemente precisa como para guiar una nave espacial hasta su destino. Para ello se necesitan métodos numéricos.
La formulación de variable universal
Para abordar las deficiencias computacionales de los enfoques tradicionales para resolver el problema de los 2 cuerpos, se desarrolló la formulación de la variable universal. Funciona igual de bien para los casos circular, elíptico, parabólico e hiperbólico, y las ecuaciones diferenciales convergen bien cuando se integran para cualquier órbita. También se generaliza bien a problemas que incorporan teoría de perturbaciones.
Perturbaciones
La formulación de variable universal funciona bien con la técnica de variación de parámetros, excepto que ahora, en lugar de los seis elementos orbitales keplerianos, utilizamos un conjunto diferente de elementos orbitales: a saber, la posición inicial del satélite y los vectores de velocidad y en un instante dado . En una simulación de dos cuerpos, estos elementos son suficientes para calcular la posición y la velocidad del satélite en cualquier momento del futuro, utilizando la formulación de variable universal. A la inversa, en cualquier momento de la órbita del satélite, podemos medir su posición y velocidad, y luego usar la aproximación de la variable universal para determinar cuál habría sido su posición y velocidad iniciales en ese momento. En un movimiento perfecto de dos cuerpos, estos elementos orbitales serían invariantes (al igual que los elementos keplerianos).
Sin embargo, las perturbaciones hacen que los elementos orbitales cambien con el tiempo. De ahí que escribamos el elemento de posición como y el elemento de velocidad como , indicando que varían con el tiempo. La técnica para calcular el efecto de las perturbaciones consiste en encontrar expresiones, exactas o aproximadas, para las funciones y .
Los siguientes son algunos efectos que hacen que las órbitas reales difieran de los modelos simples basados en una Tierra esférica. La mayoría de ellos pueden ser manejados en escalas de tiempo cortas (tal vez menos de unos pocos miles de órbitas) por la teoría de perturbaciones, ya que son pequeños en relación con los correspondientes efectos de dos cuerpos.
- Las protuberancias ecuatoriales causan la precesión del nodo y el perigeo.
- Armónicos teselares[4] del campo gravitatorio introducen perturbaciones adicionales
- Las perturbaciones gravitatorias lunares y solares alteran las órbitas
- El arrastre atmosférico reduce el semieje mayor a menos que se utilice empuje de reposición.
En escalas de tiempo muy largas (quizás millones de órbitas), incluso las pequeñas perturbaciones pueden dominar, y el comportamiento puede llegar a ser caótico. Por otro lado, los astrodinamistas inteligentes pueden orquestar las distintas perturbaciones para ayudar en las tareas de mantenimiento de la órbita, como el mantenimiento de estaciones, el mantenimiento o ajuste de pistas en tierra, o la sincronización del perigeo para cubrir objetivos seleccionados a baja altitud.
Leyes de astrodinámica
Las leyes fundamentales de la astrodinámica son la ley de Newton de la gravitación universal y las leyes de Newton del movimiento, mientras que la herramienta matemática fundamental es su cálculo diferencial.
Cada órbita y trayectoria fuera de las atmósferas es en principio reversible, es decir, en la función espacio-tiempo, el tiempo se invierte. Las velocidades se invierten y las aceleraciones son las mismas, incluidas las debidas a explosiones de cohetes. Por lo tanto, si una ráfaga de cohetes está en la dirección de la velocidad, en el caso invertido es opuesta a la velocidad. Por supuesto, en el caso de explosiones de cohetes no hay inversión total de eventos, en ambos sentidos se utiliza el mismo delta-v y se aplica la misma proporción de masa.
Las asunciones estándar en astrodinámica incluyen la no interferencia de cuerpos externos, la masa insignificante para uno de los cuerpos, y otras fuerzas insignificantes (tales como del viento solar, arrastre atmosférico, etc.). Se pueden hacer cálculos más precisos sin estas suposiciones simplificadoras, pero son más complicados. La mayor exactitud a menudo no hace suficiente diferencia en el cálculo para valer la pena.
Las leyes de Kepler del movimiento planetario pueden derivarse de las leyes de Newton, cuando se supone que el cuerpo en órbita está sujeto solamente a la fuerza gravitacional del atractor central. Cuando un empuje del motor o la fuerza propulsora está presente, las leyes de Newton todavía se aplican, pero las leyes de Kepler son invalidadas. Cuando el empuje se detiene, la órbita resultante será diferente, pero una vez más será descrita por las leyes de Kepler. Las tres leyes son:
- La órbita de cada planeta es una elipse con el sol en uno de los focos.
- Una línea que une un planeta y el sol barre áreas iguales durante intervalos iguales de tiempo.
- Los cuadrados de los períodos orbitales de los planetas son directamente proporcionales a los cubos del eje semi-mayor de las órbitas.
Maniobra orbital
En el vuelo espacial, una maniobra orbital es el uso de sistemas de propulsión para cambiar la órbita de una nave espacial. Para las naves espaciales lejos de la Tierra -por ejemplo las que están en órbitas alrededor del Sol- una maniobra orbital se denomina maniobra en el espacio profundo (DSM).
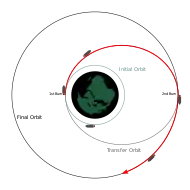
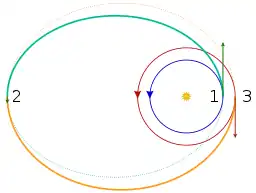
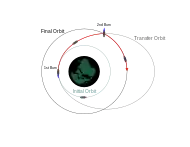
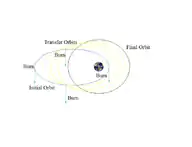
Transferencia orbital
Las órbitas de transferencia suelen ser órbitas elípticas que permiten que las naves espaciales se muevan de una órbita (generalmente circular) a otra. Por lo general, requieren un impulso al principio, un impulso al final, y a veces uno o más impulsos en el medio.
- La órbita de transferencia de Hohmann requiere un mínimo de delta-v.
- Una transferencia bielíptica puede requerir menos energía que la transferencia de Hohmann, si la relación de órbitas es 11,94 o mayor,,[5] pero se produce a costa de un aumento del tiempo de disparo durante la transferencia de Hohmann.
- Las transferencias más rápidas pueden utilizar cualquier órbita que cruce las órbitas originales y de destino, a costa de un mayor delta-v.
- Utilizando motores de empuje bajo (como la propulsión eléctrica), si la órbita inicial es supersincrónico a la órbita circular deseada final entonces la órbita de transferencia óptima se alcanza empujando continuamente en la dirección de la velocidad en el apogeo. Este método, sin embargo, toma mucho más tiempo debido al bajo empuje.[6]
Para el caso de la transferencia orbital entre órbitas no coplanares, el empuje de cambio de plano debe hacerse en el punto donde los planos orbitales se intersecan (el "nodo").

Asistencia gravitatoria y efecto Oberth
En una asistencia por gravedad, una nave espacial oscila por un planeta y sale en una dirección diferente, a una velocidad diferente. Esto es útil para acelerar o ralentizar una nave espacial en lugar de transportar más combustible.
Esta maniobra puede ser aproximada por una colisión elástica a grandes distancias, aunque el sobrevuelo no implica ningún contacto físico. Debido a la tercera ley de Newton (reacción igual y opuesta), cualquier impulso ganado por una nave espacial debe ser perdido por el planeta, o viceversa. Sin embargo, debido a que el planeta es mucho más masivo que la nave espacial, el efecto en la órbita del planeta es insignificante.
El efecto Oberth se puede emplear, particularmente durante una operación de asistencia por gravedad. Este efecto es que el uso de un sistema de propulsión funciona mejor a altas velocidades y, por lo tanto, los cambios de rumbo se hacen mejor cuando están cerca de un cuerpo gravitatorio; Esto puede multiplicar el delta-v eficaz.
Red de Transporte Interplanetario y órbitas difusas
Ahora es posible usar computadoras para buscar rutas usando las no linealidades en la gravedad de los planetas y lunas del Sistema Solar. Por ejemplo, es posible trazar una órbita desde la órbita terrestre alta hasta Marte, pasando cerca de uno de los puntos troyanos de la Tierra. Colectivamente denominada Red Interplanetaria de Transporte, estas trayectorias orbitales altamente perturbadoras, incluso caóticas, no necesitan más combustible que el necesario para alcanzar el punto de Lagrange (en la práctica, mantener la trayectoria requiere algunas correcciones de rumbo). El mayor problema con ellos es que pueden ser muy lento, teniendo muchos años. Además, las ventanas de lanzamiento pueden estar muy separadas.
Sin embargo, se han empleado en proyectos como Génesis. Esta nave espacial visitó el punto Tierra-Sol L1 y volvió usando muy poco propulsor.
Referencias
- Thomson, William T. (1961). Introduction to Space Dynamics. New York: Wiley.
- Bate, R. R.; Mueller, D. D.; White, J. E. (1971). Fundamentos de Astrodinámica. Courier Corporation. p. 5. ISBN 978-0-486-60061-1.
- Negri, Rodolfo Batista; Prado, Antônio Fernando Bertachini de Alme (Agosto 2020). «Revisión histórica de la teoría de las asistencias gravitatorias en la era pre-vuelo espacial». Journal de la Sociedad Brasileña de Ciencias Mecánicas e Ingeniería 42 (8): 406. S2CID 220510617.
- Weisstein, Eric W. «Tesseral Harmonic». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Vallado, David Anthony (2001). Fundamentals of Astrodynamics and Applications. Springer. p. 317. ISBN 0-7923-6903-3.
- Spitzer, Arnon (1997). Optimal Transfer Orbit Trajectory using Electric Propulsion. USPTO.
Bibliografía
Muchas de las opciones, procedimientos y teoría de apoyo se tratan en obras estándar como:
- Bate, R.R.; Mueller, D.D.; White, J.E. (1971). Fundamentals of Astrodynamics. Dover Publications, New York. ISBN 978-0-486-60061-1.
- Vallado, D. A. (2001). Fundamentals of Astrodynamics and Applications (2nd edición). Springer. ISBN 978-0-7923-6903-5.
- Battin, R.H. (1999). An Introduction to the Mathematics and Methods of Astrodynamics. American Institute of Aeronautics & Ast, Washington, D.C. ISBN 978-1-56347-342-5.
- Chobotov, V.A., ed. (2002). Orbital Mechanics (3rd edición). American Institute of Aeronautics & Ast, Washington, D.C. ISBN 978-1-56347-537-5.
- Herrick, S. (1971). Astrodynamics: Orbit Determination, Space Navigation, Celestial Mechanics, Volume 1. Van Nostrand Reinhold, London. ISBN 978-0-442-03370-5.
- Herrick, S. (1972). Astrodynamics: Orbit Correction, Perturbation Theory, Integration, Volume 2. Van Nostrand Reinhold, London. ISBN 978-0-442-03371-2.
- Kaplan, M.H. (1976). Modern Spacecraft Dynamics and Controls. Wiley, New York. ISBN 978-0-471-45703-9.
- Tom Logsdon (1997). Orbital Mechanics. Wiley-Interscience, New York. ISBN 978-0-471-14636-0.
- John E. Prussing; Bruce A. Conway (1993). Orbital Mechanics. Oxford University Press, New York. ISBN 978-0-19-507834-3. Parámetro desconocido
|name-list-style=ignorado (ayuda) - M.J. Sidi (2000). Spacecraft Dynamics and Control. Cambridge University Press, New York. ISBN 978-0-521-78780-2.
- W.E. Wiesel (1996). Spaceflight Dynamics (2nd edición). McGraw-Hill, New York. ISBN 978-0-07-070110-6.
- J.P. Vinti (1998). Orbital and Celestial Mechanics. American Institute of Aeronautics & Ast, Reston, Virginia. ISBN 978-1-56347-256-5.
- P. Gurfil (2006). Modern Astrodynamics. Butterworth-Heinemann. ISBN 978-0-12-373562-1.
Enlaces externos
- ORBITAL MECHANICS (Rocket and Space Technology)
- Java Astrodynamics Toolkit
- Astrodynamics-based Space Traffic and Event Knowledge Graph