Mecanismo de Anticitera
El mecanismo de Anticitera es una computadora analógica[1][2][3][4] (o mecánica) de la antigüedad. Supuestamente construido por científicos griegos, el instrumento se data entre los años 150 a. C. y 100 a. C.,[5] o, según una observación reciente, hacia el año 200 a. C.[6][7] El componente fue recuperado en el mar Egeo, entre los años 1900 y 1901, de un antiguo naufragio cercano a la isla griega de Anticitera.[8] Este artefacto aparentemente fue diseñado para predecir posiciones astronómicas y los eclipses de hasta diecinueve años con propósitos astrológicos y calendáricos,[5][9][10] y predecir también la fecha exacta de seis certámenes griegos antiguos, entre los que se encuentran los cuatro principales juegos Panhelénicos y dos juegos más de menor entidad.[11][12]




Se debía encontrar alojado en una caja de madera cuyas dimensiones eran de 340 por 180 por 90 milímetros; el dispositivo es un complejo mecanismo de relojería compuesto de al menos 30 engranajes de bronce. Los restos fueron encontrados como 82 fragmentos separados, de los cuales solo siete contenían inscripciones importantes o engranajes.[13][14] El engranaje más grande (claramente visible en el fragmento A a la derecha) mide aproximadamente 140 mm de diámetro y originalmente contaba con 223 dientes.[15]
Es probable que el mecanismo de Anticitera no fuera el único, como muestran las referencias de Cicerón sobre estos mecanismos. Esto da soporte a la idea de que hubo una tradición en la antigua Grecia de tecnología mecánica compleja. Todos los fragmentos recuperados del mecanismo de Anticitera se custodian en el Museo Arqueológico Nacional de Atenas.[16]
En De re publica, Cicerón hace mención a dos máquinas diseñadas y construidas por Arquímedes, que los analistas contemporáneos consideran que eran mecanismos de tipo planetario, predictores de los movimientos de la Luna, el Sol, los principales planetas conocidos y los eclipses. Estas máquinas pasaron a poder del cónsul romano Marco Claudio Marcelo tras el sitio de Siracusa, hecho ocurrido en 212 a. C.[17]
La expansión de esta tecnología se interrumpió en algún momento de la antigüedad, y artefactos tecnológicos que se acercaran a la complejidad y habilidad de construcción de este instrumento no aparecieron nuevamente hasta 1600 años después, época en que se inició el desarrollo de relojes astronómicos en Europa, hacia el siglo XIV.[18]
Historia
Descubrimiento
El mecanismo de Anticitera fue descubierto a 45 metros bajo el agua cerca de Glyfadia, en la isla griega de Anticitera. Los restos del antiguo naufragio se encontraron en abril de 1900 por parte de un grupo de buzos recolectores de esponjas; estos recuperaron numerosos artefactos, incluyendo estatuas de bronce y mármol, alfarería, vidriería, joyería, monedas y el mecanismo. Los hallazgos fueron enviados al Museo Arqueológico Nacional de Atenas para su análisis y almacenamiento. El mecanismo pasó inadvertido durante dos años como un bulto de bronce corroído y madera hasta que el equipo del museo empezó a unir las piezas más obvias del mecanismo.[18]
El 17 de mayo de 1902, cuando el arqueólogo Valerios Stais examinaba los restos se dio cuenta de que una de las piezas de roca tenía un engranaje incrustado. Stais, inicialmente, creyó que se trataba de un reloj astronómico pero la mayoría del equipo creía que el instrumento era tecnológicamente muy avanzado y muy complejo como para haber sido construido en la misma época que el resto de las piezas encontradas. Las investigaciones fueron abandonadas hasta que el instrumento captó la atención de Derek John de Solla Price en 1951.[19] En 1971, Price y un físico nuclear llamado Charalampos Karakalos analizaron los 82 fragmentos con rayos X y rayos gamma. Price publicó un extensivo ensayo de 70 páginas sobre los resultados en 1974.[18]
Se desconoce cómo llegó el mecanismo al barco, pero se ha propuesto que se planeaba llevar el instrumento a Roma con el resto del botín para la celebración del triunfo de Julio César.[20]
Investigaciones sobre su cronología y origen
Aunque generalmente es referido como la primera computadora analógica,[21] la calidad y complejidad de la manufactura del mecanismo sugieren que este tiene predecesores aún no descubiertos hechos en el periodo helenístico.[22] Su construcción está basada en teorías de la astronomía y matemáticas desarrolladas por astrónomos griegos.[5] La estimación sobre la fecha de fabricación que hace el museo de Atenas es que debe de pertenecer a la segunda mitad del siglo II a. C, principalmente basada en el análisis epigráfico de los textos conservados.[23]
En 1974, el historiador de la ciencia británico y profesor de la Universidad Yale Derek John de Solla Price concluyó, gracias a ajustes de los engranajes y a inscripciones en las caras del mecanismo, que el instrumento fue hecho alrededor del año 87 a. C. y perdido pocos años después.[8] Jacques Cousteau y sus asociados visitaron el naufragio en 1976[24] y recuperaron monedas que dataron entre los años 76 y 67 a. C.[25] A pesar de que el avanzado estado de corrosión ha vuelto imposible la realización de un análisis de su composición, se cree que el dispositivo está hecho de una aleación de cobre y estaño (aproximadamente 95 % cobre y 5 % estaño).[26] Las instrucciones de uso están escritas en koiné con rasgos dialectales corintios y la creencia que se impone entre los profesionales es la de que el mecanismo fue creado en el mundo de habla griega.[9]
Los resultados de los estudios llevados a cabo a partir de 2005 por el Proyecto de Investigación del Mecanismo de Anticitera sugieren que el concepto del mecanismo se originó en las colonias de Corinto, ya que el dialecto de las inscripciones así lo determina. Más en concreto, Siracusa era una muy próspera antigua colonia de Corinto y el hogar del gran ingeniero Arquímedes, lo que podría implicar una conexión con la escuela de Arquímedes.[11] Otra teoría sugiere que las monedas encontradas por Jacques Cousteau en la década de los 70 en el naufragio se remontan a la época en que se construyó el mecanismo y su origen es la ciudad griega de Pérgamo,[27] hogar de la famosa Biblioteca de Pérgamo. Gracias a la cantidad de manuscritos sobre ciencia y arte, es la segunda biblioteca más importante, después de la Biblioteca de Alejandría, del periodo helenístico.[28]
El navío que transportaba el mecanismo también llevaba vasijas con un estilo proveniente de Rodas; esto lleva a la creencia de que el mecanismo fue construido en una academia fundada por el estoico filósofo Posidonio en esa isla griega. Rodas era un puerto comercial con mucho tráfico y también era un centro de ingeniería astronómica y mecánica, hogar de Hiparco de Nicea, quien estuvo activo desde el año 140 a. C. hasta el año 120 a. C. El hecho de que el mecanismo recurra a la teoría de Hiparco sobre el movimiento de la Luna indica que él pudo haberlo diseñado o contribuido en su construcción.[18]
En el año 2014, un estudio conducido por Carman y Evans argumentaba que el origen del mecanismo era en realidad el año 200 a. C.[6][7] Según Carman y Evans, el estilo de predicción aritmética babilónico encaja mejor con el modelo predictivo del mecanismo que el estilo trigonométrico tradicional griego.[6]
En un estudio publicado en 2017, Paul Iversen sostiene que el mecanismo de Anticitera fue un dispositivo creado para un cliente de Epiro a partir de un prototipo que originalmente había sido realizado para ser usado en la isla de Rodas.[29]: 192
Descripción
Aparentemente, el mecanismo original abandonó el Mediterráneo como una sola pieza incrustada; poco después se fracturó en tres piezas principales. Diversas piezas pequeñas del interior se han roto mientras se manipulaba o limpiaba el mecanismo y otras fueron encontradas en el suelo marino por la expedición de Cousteau. Existe la posibilidad de que haya más fragmentos almacenados desde el descubrimiento del mecanismo y aún no se hayan descubierto; el fragmento F salió a la luz de esa manera en el año 2005. De los 82 fragmentos, 7 son mecánicamente significativos y contienen la mayoría de las inscripciones del mecanismo; existen otros 16 fragmentos que contienen inscripciones parciales e incompletas.[5][30][31]
Fragmentos mayores
| Fragmento | Tamaño [mm] | Peso [g] | Engranes | Inscripciones | Notas |
|---|---|---|---|---|---|
| A | 180 × 150 | 369.1 | 27 | ✔ | Es el fragmento principal y contiene la mayor parte conocida del mecanismo. El engranaje b1 es claramente visible en el frente y, detrás de este, se pueden apreciar más engranajes al observar cuidadosamente (partes de los engranajes l, m, c y d son visibles a simple vista). La cuenca del mecanismo de manivela y el engranaje lateral conectado a b1 está en este fragmento. El reverso del fragmento contiene los engranajes e y k para la síntesis de la anomalía lunar; también es visible el mecanismo de perno y muesca en el engranaje k. Por medio de escaneos se aprecia que los engranajes están estrechamente empaquetados y han recibido daños y desplazamientos con el tiempo en el mar. El fragmento es aproximadamente 30 mm de grueso en el punto más ancho.
El fragmento contiene la división del cuarto superior izquierdo del espiral de Saros y 14 inscripciones del mismo. También contiene inscripciones para el disco de exeligmos y restos de la cara del disco. |
| B | 125 × 60 | 99.4 | 1 | ✔ | Contiene aproximadamente el tercio inferior derecho del espiral metónico e inscripciones del espiral y de la puerta trasera. La escala metónica consistiría de 235 celdas, de las cuales 49 han sido descifradas del fragmento B, ya sea completa o parcialmente. Se deduce el resto con el conocimiento del ciclo metónico. Este contiene un solo engranaje (o1) usado en el sistema olímpico. |
| C | 120 × 110 | 63.8 | 1 | ✔ | Contiene partes del extremo derecho de la cara frontal del disco con inscripciones zodiacales y del calendario visibles. También contiene el ensamblaje del disco indicador lunar incluyendo la esfera de fase lunar en su cubierta y un único engranaje biselado (ma1) usado en el sistema de indicación de fase lunar. |
| D | 45 × 35 | 15.0 | 1 | Contiene al menos un engranaje desconocido y posiblemente dos según Michael T. Wright. El propósito de estos no ha sido atribuido a ninguna función, pero se cree que influyen en la posible visualización de los planetas en la cara frontal del mecanismo. | |
| E | 60 × 35 | 22.1 | ✔ | Encontrado en el año 1976, contiene 6 inscripciones del lado superior derecho del espiral de Saros. | |
| F | 90 × 80 | 86.2 | X | Encontrado en el año 2005, contiene 16 inscripciones del lado inferior derecho del espiral de Saros. También contiene restos de la cubierta de madera del mecanismo. | |
| G | 125 × 110 | 31.7 | ✔ | Una combinación de fragmentos obtenidos de C mientras este se limpiaba. |
Fragmentos menores
Muchos de los fragmentos más pequeños que han sido encontrados no contienen nada de valor; sin embargo, dieciséis de ellos tienen inscripciones. Algunas de ellas, que anteriormente se pensaba que podrían describir instrucciones sobre la función de los discos traseros, en realidad solo contienen descripciones de los mismos.[32]: 7, 8 La ausencia de instrucciones hace suponer que la persona a la que fuera a destinarse el mecanismo estaba bien instruida en astronomía.[33]
Mecanismo
Operación

En la cara frontal del mecanismo (ver reproducción aquí:[34]) se encuentra un disco en forma de anillo, fijado a la estructura, que representa la eclíptica y los 12 signos zodiacales marcados en sectores de 30 grados. Esto concuerda con la costumbre babilónica de asignar un doceavo de la eclíptica a cada signo zodiacal equitativamente, aunque los límites de las constelaciones eran variables. Fuera del disco se encuentra otro anillo que es giratorio; este está marcado con los meses y días del calendario egipcio: 12 meses de 30 días más 5 días epagomenales. Los meses están marcados con sus respectivos nombres egipcios transcritos al alfabeto griego. La primera tarea es rotar el calendario egipcio para concordar los signos del zodíaco en el artefacto con los actuales. El calendario egipcio ignoraba los 5 días epagomenales, por lo que avanzaba completamente por un símbolo zodiacal en aproximadamente 120 años.[9]
El mecanismo era operado mediante la rotación de una manivela (actualmente perdida) que se conectaba por medio de un engranaje en forma de corona al engrane de mayor tamaño, el engranaje con cuatro dientes en el frente del fragmento ha sido llamado B1. Esto movía el cursor en el disco frontal que seleccionaría el día correcto del calendario egipcio. El año no era seleccionable, por lo que era necesario saber el año actualmente seleccionado o buscar los ciclos con ayuda de los diversos indicadores de ciclo del calendario en el reverso de las tablas babilónicas de efemérides por el día del año seleccionado, ya que los ciclos del calendario no son sincrónicos con el año. La manivela movía el cursor de fecha por 78 días cada rotación completa; esto facilitaba la selección de un día particular si el mecanismo se encontraba en buenas condiciones. La acción de girar la manija de la manivela causaría que los engranajes interconectados dentro del mecanismo rotaran; esto resultaba en el cálculo simultáneo de la posición del Sol y la Luna, la fase lunar, eclipse, ciclos del calendario y posiblemente la posición de planetas.[35]
El operador también debía estar al tanto de la posición de los cursores del selector espiral en los dos discos al reverso del mecanismo. El cursor tenía un “seguidor” que rastreaba las incisiones espirales en el metal según los discos incorporaran 4 o 5 rotaciones completas del cursor. Cuando un cursor alcanzaba la posición de un mes terminal al final del espiral, el seguidor del cursor debía ser movido manualmente al otro extremo del espiral antes de poder continuar el funcionamiento.[5]: 10
Cara anterior
El disco frontal tiene dos escalas circulares concéntricas que representan el camino a través de los cielos. El anillo exterior está marcado con los 365 días del calendario egipcio o el año Sotíaco basado en el ciclo Sotíaco. En el anillo interno hay un segundo disco marcado con los signos zodiacales griegos y se divide en grados. El calendario exterior no estaba fijado totalmente con el disco interior, sino que para compensar el efecto del cuarto de día adicional en el año solar, el operador del mecanismo podía moverlo hacia atrás en relación con el interior un día cada 4 años.[36]
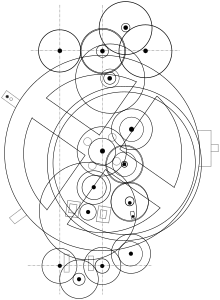
La posición del Sol en la eclíptica es equivalente a la fecha actual en el año. La Luna y los cinco planetas conocidos por los griegos viajan a lo largo de la eclíptica cercanamente entre sí mismos, tan cerca que tenía sentido definir su posición en la eclíptica.
Los siguientes meses egipcios están inscritos en el anillo exterior:
- ΘΟΘ (Thoth)
- ΦΑΩΦΙ (Phaophi)
- ΑΟΤΡ (Athyr, Hathor)
- ΧΟΙΑΚ (Choiak)
- ΤΥΒΙ (Tybi)
- ΜΕΧΕΙΡ (Mecheir)
- ΦΑΜΕΝΩΘ (Phamenoth)
- ΦΑΡΜΟΥΘΙ (Pharmouthi)
- ΠΑΧΩΝ (Pachon)
- ΠΑΥΝΙ (Payni)
- ΕΠΙΦΙ (Epiphi)
- ΜΕΣΟΡΗ (Mesore)
- ΕΠ (Ep[agomene])
El disco zodiacal contenía inscripciones griegas de los miembros del zodiaco; esto se supone que era para adaptarse con la versión del mes tropical en vez de la del mes sideral:[32]: 8
- ΚΡIOΣ (Krios [Carnero], Aries)
- ΤΑΥΡΟΣ (Tauros [Toro], Tauro)
- ΔIΔΥΜΟΙ (Didymoi [Gemelos], Géminis)
- ΚΑΡΚIΝΟΣ (Karkinos [Cangrejo], Cáncer)
- ΛEΩΝ (Leon [León], Leo)
- ΠΑΡΘEΝΟΣ (Parthenos [Virgen], Virgo)
- ΧΗΛΑΙ (Chelai [Garra de Escorpión o Zygos], Libra)
- ΣΚΟΡΠΙΟΣ (Skorpios [Escorpión], Escorpio)
- ΤΟΞΩΤΗΣ (Toxotes [Arquero], Sagitario)
- ΑIΓOΚΕΡΩΣ (Aigokeros [cabra], Capricornio)
- YΔΡΟΚΟΟΣ (Hydrokoos [Cargador de Agua], Acuario)
- IΧΘΕIΣ (Ichtheis [Pez], Piscis)
En los discos zodiacales también se encuentran caracteres únicos en ciertos puntos (ver reconstrucción aquí:[34]). Están relacionados con un almanaque griego, precursor del almanaque moderno inscrito en la cara frontal detrás de los discos. Estos marcan las ubicaciones y longitudes de la eclíptica para estrellas específicas. Partes del almanaque griego leen (las llaves indican el texto inferido):
- {Κ} Noche
- {Λ} La puesta de las Híades en la noche
- {Μ} Tauro comienza a elevarse
- {N} Vega se elevan en la noche
- {Θ} Las Pléyades se elevan en la mañana.
- {Ο} Las Híades se elevan en la mañana
- {Π} Géminis comienza a elevarse
- {Ρ} Altair se eleva en la mañana
- {Σ} La puesta de Arturo en la mañana
Al menos dos cursores indican la posición de cuerpos sobre la eclíptica. Un cursor lunar indica la posición de la Luna y también se observa un cursor aproximado solar. La posición lunar no estaba simplemente aproximada, ya que el indicador no describía un movimiento uniforme sino que tomaba en cuenta la aceleración y desaceleración típica de lo que se conoce hoy como órbita elíptica, todo esto mediante el primer uso conocido de un engranaje planetario.
También rastreaba la precesión de la órbita elíptica alrededor de la eclíptica en un ciclo de 8,88 años. La posición aproximada del Sol es, por definición, la fecha actual. Se especula que, con todo el esfuerzo dedicado para representar la posición real de la Luna[32]: 20, 24 , habría una precisión similar para el Sol; a la fecha no se ha encontrado evidencia de esto.[9] De manera similar, no se encuentra evidencia de cursores de la órbita planetaria, para los cinco planetas conocidos por los griegos, entre los restos.
Por último, el ingeniero mecánico Michael Wright demostró que hay un mecanismo para mostrar la fase lunar al igual que su posición.[37] El indicador es una pequeña esfera embebida al cursor lunar, mitad blanca y mitad negra, que rotaba para representar la fase lunar (luna nueva, primer cuarto, mitad, tercer cuarto, luna llena y luna negra) gráficamente. La información para mostrar esta función está disponible dadas las posiciones del Sol y la Luna como rotaciones angulares; en esencia es el ángulo entre los dos, traducido en la rotación de la esfera. Se requiere de un diferencial, un arreglo de engranes que acumula o diferencia dos entradas angulares. El mecanismo de Anticitera es históricamente la primera construcción deliberada de un diferencial que se conoce.[38]
Cara posterior
En el reverso del mecanismo se encuentran al menos cuatro discos: los dos grandes calculan el ciclo metónico y de Saros, mientras que los dos pequeños son para los juegos deportivos,[30] y exeligmos.[5]: 11 Es posible que también hubiera dos discos más, uno para el ciclo calípico, simétrico al de los juegos y otro simétrico al de exeligmos, pero ninguno de estos dos últimos ha podido ser confirmado por las investigaciones.[30]: 4
El disco metónico se encuentra en el lado superior del mecanismo. El ciclo metónico, definido en varias unidades físicas, es de 235 meses sinódicos, lo que es muy cercano (en menos de 13 millonésimas) a los 19 años tropicales. Es por esto que este es un intervalo conveniente al cual convertir entre el calendario lunar o solar. El disco metónico cubre 235 meses en cinco rotaciones del disco; lo hace siguiendo una pista espiral con un seguidor en el cursor que rastrea la capa del espiral. El cursor indica el mes sinódico, contado de luna nueva a luna nueva, y la celda contiene los nombres de los meses en el calendario corintio[39] o en otro calendario derivado de este, que podría ser el epirota.[29]: 129
- ΦΟΙΝΙΚΑΙΟΣ (Feniceo)
- ΚΡΑΝΕΙΟΣ (Cranio)
- ΛΑΝΟΤΡΟΠΙΟΣ (Lanotropio)
- ΜΑΧΑΝΕΥΣ (Macaneo)
- ΔΩΔΕΚΑΤΕΥΣ (Dodecateo)
- ΕΥΚΛΕΙΟΣ (Eucleio)
- ΑΡΤΕΜΙΣΙΟΣ (Artemisio)
- ΨΥΔΡΕΥΣ (Psydreo)
- ΓΑΜΕΙΛΙΟΣ (Gamilio)
- ΑΓΡΙΑΝΙΟΣ (Agrianio)
- ΠΑΝΑΜΟΣ (Panamo)
- ΑΠΕΛΛΑΙΟΣ (Apeleo)
Por tanto, la configuración de la fecha solar correcta en el panel frontal indica el mes lunar actual en el panel del reverso con resolución de aproximadamente una semana.
Anteriormente se creía que el disco calípico —un ciclo de 76 años que comprende, por tanto, cuatro ciclos metónicos— era el disco superior secundario que estaban dentro del disco metónico, pero las investigaciones publicadas en 2008 establecieron que en realidad ese disco superior secundario era el que indicaba los juegos panhelénicos. No obstante, la inscripción 76 años del fragmento 19 es un indicio de que podría haber otro hipotético disco que indicara el ciclo calípico y que sería simétrico al disco de los juegos.[30]: 4
El disco de los juegos es el disco superior derecho secundario; es el único cursor en el instrumento que viaja opuestamente a las manecillas del reloj con el paso del tiempo. El disco se divide en cuatro sectores; cada uno tiene un indicador de año y el nombre de dos Juegos Panhelénicos. Estos eran los Juegos Ístmicos, los Juegos Olímpicos, los Juegos Nemeos y los Juegos Píticos y también incluyen juegos menores como los Juegos cuatrienales de las Naia (con sede en Dodona y en honor de Dione Naia) y otro evento que podría tratarse del festival de la Halieia, de Rodas.[29]: 130 Las inscripciones en cada una de las cuatro divisiones son:[5]: 4–5, 10 [30]
| Año del ciclo | Inscripción dentro del disco | Inscripción fuera del disco |
|---|---|---|
| 1 | LA | ΙΣΘΜΙΑ (Ístmia) ΟΛΥΜΠΙΑ (Olimpia) |
| 2 | LB | NEMEA (Nemea) NAA (Naa) |
| 3 | LΓ | ΙΣΘΜΙΑ (Ístmia) ΠΥΘΙΑ (Pitia) |
| 4 | L∆ | ΝΕΜΕΑ (Nemea) ΑΛΙEΙΑ[29]: 141 |
El disco de Saros es el disco espiral inferior principal en el reverso del mecanismo.[5]: 4–5, 10 El ciclo de Saros consta de 18 años y 11 1⁄3 días (6585,333… días), lo cual se aproxima bastante a los 223 meses sinódicos (6585,3211 días). Está definido como el ciclo de repetición de las posiciones necesitadas para formar los eclipses solares y lunares; por lo tanto, se podía usar para predecir los eclipses no a nivel de mes o día sino que a tiempo del día. Nótese que un ciclo es aproximadamente 8 horas más largo que un número entero de días. Al traducir esto en rotación global, significa que el eclipse ocurrirá no solo 8 horas después sino que también un tercio de rotación más al este. Glifos encontrados en 51 de las 223 celdas de mes sinódico del disco especifican la ocurrencia de 38 eclipses lunares y 27 eclipses solares. Algunas de las abreviaciones en los glifos dicen:
- Σ = ΣΕΛΗΝΗ (Luna)
- Η = ΗΛΙΟΣ (Sol)
- H\M = ΗΜΕΡΑΣ (del día)
- ω\ρ = ωρα (hora)
- N\Y = ΝΥΚΤΟΣ (de la noche)
Los glifos indican si el eclipse designado es lunar o solar, da la fecha del día del mes y la hora, ya que los eclipses solares no son visibles en cualquier momento, y los eclipses lunares solo son visibles si la Luna está sobre el horizonte en la hora indicada.[32]: 6
El disco de exeligmos es el disco secundario inferior derecho en el reverso del mecanismo. El ciclo de exeligmos consiste de tres ciclos de Saros con un total de 54 años; esto significa que dura 19,756 días. Como la duración del ciclo de Saros es de 8 horas, un ciclo completo de exeligmos muestra el conteo en días enteros. Por esto tiene inscripciones como:[5]: 10
- Vacío (representa el cero)
- H (número 8)
- Iϛ (número 16)
Como resultado, el disco indica cuántas horas deben ser añadidas a los tiempos de los glifos del disco de Saros para poder calcular tiempos exactos de eclipses.
Puertas
El mecanismo tiene una cubierta hecha de madera con una puerta frontal y otra trasera; ambas contienen inscripciones.[32] La puerta trasera parece ser el “Manual de Instrucciones”. En uno de los fragmentos —el denominado fragmento 19— se lee “76 años, 19 años”, que se refieren a los ciclos calípico y metónico. También se aprecia la inscripción “223” para los ciclos de Saros. En otro de los fragmentos está escrito, en las subdivisiones espirales, “235” para el disco metónico.[30]: 11, 12
Engranaje
El mecanismo es extraordinario en cuanto a su nivel de miniaturización y complejidad de sus partes; es comparable a los relojes astronómicos del siglo XIV. Tiene al menos 30 engranajes, aunque el experto Michael T. Wright sugiere que los griegos de aquella época eran capaces de implementar más.[35]
Hay mucha controversia sobre la capacidad del mecanismo de predecir las posiciones de los planetas conocidos por los griegos en aquella época. No se ha encontrado ningún conjunto de engranajes dedicados a tal tarea a excepción de un engranaje de 63 dientes (g1) en el fragmento D al que no se le ha encontrado otra función.[9]
El propósito de la cara frontal era posicionar los cuerpos astronómicos respecto a la esfera celeste a lo largo de la eclíptica desde el punto de vista de un observador en la Tierra. Eso es irrelevante al preguntarse si la posición era calculada usando una vista heliocéntrica o geocéntrica del Sistema solar; cualquiera que se haya usado resultaría en la misma posición (ignorando la elipticidad) dentro del rango de error del mecanismo.
El sistema solar epicíclico de Ptolomeo (300 años en el futuro de la fecha aparente del mecanismo) funcionaba con más epiciclos; era más preciso al predecir las posiciones de los planetas que Copérnico hasta que Kepler introdujo la posibilidad de que las órbitas fuesen elipses.[40]
Evans propuso que para poder mostrar las posiciones aproximadas de los planetas requeriría de 17 engranajes adicionales para ser posicionados al frente del engranaje principal y usando discos circulares individuales en la misma cara.[41]
Tony Freeth y Alexander Jones han modelado y publicado una versión usando varios engranajes mecánicamente similares al sistema de anomalía lunar permitiendo la indicación de posiciones planetarias al igual que la síntesis de la anomalía solar. Según Freeth y Jones, su sistema es más auténtico que el modelo de Wright, ya que el suyo exige habilidades que los griegos de aquella época poseían y no agrega complejidad adicional o estrés interno a la máquina.[9]
Los dientes de los engranajes eran triángulos equiláteros con una inclinación circular promedio de 1,6 mm; el grueso promedio de la rueda era de 1,4 mm y el espacio entre engranajes promedio era de 1,2 mm. Los dientes fueron hechos, probablemente, de un disco de bronce usando herramientas de mano; esto es evidente debido a que no todos son uniformes.[9] Gracias a los avances en la tecnología de rayos X, ahora es posible determinar el número de dientes y tamaño de los engranajes de los fragmentos encontrados y como resultado se conoce la operación básica del mecanismo y se ha podido replicar precisamente. Aunque persiste la duda de la existencia de los indicadores de planetas.[32]: 8
Una tabla sobre los engranajes, sus dientes y el número esperado de rotaciones de los engranajes importantes se muestra a continuación. Las funciones de los engranajes provienen de Freeth et al. (2008)[11] y aquellos de la segunda mitad de la tabla provienen de Freeth y Jones (2012).[9] Los valores calculados empiezan con una revolución del engranaje b1 y el resto se calculó de las proporciones de los dientes de los engranajes. Los engranajes marcados con un asterisco (*) no han sido encontrados o tienen predecesores perdidos; han sido calculados sobre la base de lo conocido del mecanismo con números de dientes razonables.[11][32]
| Nombre
de engrane | Función del engrane/cursor | Intervalo simulado esperado de una revolución completa | Fórmula del mecanismo | Intervalo calculado | Dirección de rotación del engrane[table 3] |
|---|---|---|---|---|---|
| X | Engrane del año | 1 año tropical | 1 (por definición) | 1 año (supuesto) | Opuesto a las manecillas del reloj[table 4] |
| B | Órbita de la Luna | 1 mes sideral (27.321661 días) | Tiempo(B) = Tiempo(X) * C1 / B2 * D1 / C2 * E2 / D2 * K1 / E5 * E6 / K2 * B3 / E1 | 27.321 días[table 5] | Opuesto a las manecillas del reloj |
| R | Fase lunar | 1 mes sinódico (29.530589 días) | Tiempo(R) = 1 / (1 / Tiempo(B2 o sun3)) - (1 / Tiempo(B))) | 29.530 días[table 5] | |
| N* | Cursor metónico | Ciclo metónico (19 años) / 5 espirales alrededor del disco= 1387.94 días | Tiempo(N) = Tiempo(X) * (L1 / B2) * (M1 /L2) * (N1 / M2) | 1387.9 días | Opuesto a las manecillas del reloj[table 6] |
| O* | Cursor Olímpico | 4 años | Tiempo(O) = Tiempo(N) * (O1 / N2) | 4.00 años | Opuesto a las manecillas del reloj[table 6][table 7] |
| Q* | Cursor calípico | 27758.8 días | Tiempo(Q) = Tiempo(N) * (P1 / N3) * (Q1 /P2) | 27758 días | Misma de las manecillas del reloj[table 6] |
| E* | Precesión lunar | 8.85 años | Tiempo(E) = Tiempo(X) * (L1 / B2) * (M1 / L2) * (E3 / M3) | 8.8826 años | Misma de las manecillas del reloj[table 8] |
| G* | Ciclo de Saros | Tiempo de Saros / 4 vueltas = 1646.33 días | Tiempo(G) = Tiempo(E) * (F1 / E4) * (G1 / F2) | 1646.3 días | Misma de las manecillas del reloj[table 6] |
| I* | Cursor de exeligmos | 19755.8 días | Tiempo(I) = Tiempo(G) * (H1 / G2) * (I1 / H2) | 19756 días | Misma de las manecillas del reloj[table 6] |
| Los siguiente engranes fueron propuestos por la reconstrucción de Freeth y Jones(2012): | |||||
| sun3* | Cursor del sol | 1 año promedio | Tiempo(sun3) = Tiempo(X) * (sun3 / sun1) * (sun2 / sun3) | 1 año promedio[table 5] | Opuesto a las manecillas del reloj[table 9] |
| mer2* | Cursor de Mercurio | 115.88 días (periodo sinódico) | Tiempo(mer2) = Tiempo(X) * (mer2 / mer1) | 115.89 días[table 5] | Opuesto a las manecillas del reloj[table 9] |
| ven2* | Cursor de Venus | 583.93 días (periodo sinódico) | Tiempo(ven2) = Tiempo(X) * (ven1 / sun1) | 584.39 días[table 5] | Opuesto a las manecillas del reloj[table 9] |
| mars4* | Cursor de Marte | 779.96 días (periodo sinódico) | Tiempo(mars4) = Tiempo(X) * (mars2 / mars1) * (mars4 / mars3) | 779.84 días[table 5] | Opuesto a las manecillas del reloj[table 9] |
| jup4* | Cursor de Júpiter | 398.88 días (periodo sinódico) | Tiempo(jup4) = Tiempo(X) * (jup2 / jup1) * (jup4 / jup3) | 398.88 días[table 5] | Opuesto a las manecillas del reloj[table 9] |
| sat4* | Cursor de Saturno | 378.09 días (periodo sinódico) | Tiempo(sat4) = Tiempo(X) * (sat2 / sat1) * (sat4 / sat3) | 378.06 días[table 5] | Opuesto a las manecillas del reloj[table 9] |
Notas de tabla:
- Cambio del nombre tradicional: X es el eje principal de año, gira una vez por año con el engrave B1. El eje B es el eje con los engranes B3 y B6 mientras que el eje E tiene los engranes E3 y E4. Otros ejes en E (E1/E6 y E2/E5) son irrelevantes en esta tabla.
- “Tiempo” es el intervalo representado por una revolución completa del engrane.
- Como visto desde el frente del mecanismo. La vista “natural” es desde el lado en el que se muestra el mecanismo del disco/cursor en cuestión.
- Estando los griegos en el hemisferio norte, el movimiento de las estrellas correcto serpia de este a oeste, es opuesto a las manecillas del reloj cuando la elíptica y el zodiaco son vistos en el sur. Como visto desde el frente del mecanismo.
- En promedio, gracias al engranaje planetario causando aceleraciones y desaceleraciones.
- Debido a su ubicación en el reverso del mecanismo, su rotación “natural” es la opuesta.
- Este era el único cursor visible viajando naturalmente en el sentido de las manecillas del reloj.
- Interno e inapreciable.
- Movimiento progrado; retrogrado es obviamente la dirección opuesta.
Hay varias proporciones de engranes para cada planeta que resulta en valores cercanos en el cálculo de periodos sinódicos de planetas y el sol. Los elegidos en la parte superior parecen ser de gran precisión con números de dientes razonables, pero los engranes específicos que pueden haber sido usados, probablemente continúen como desconocidos.[9]
Esquema de los engranes conocidos
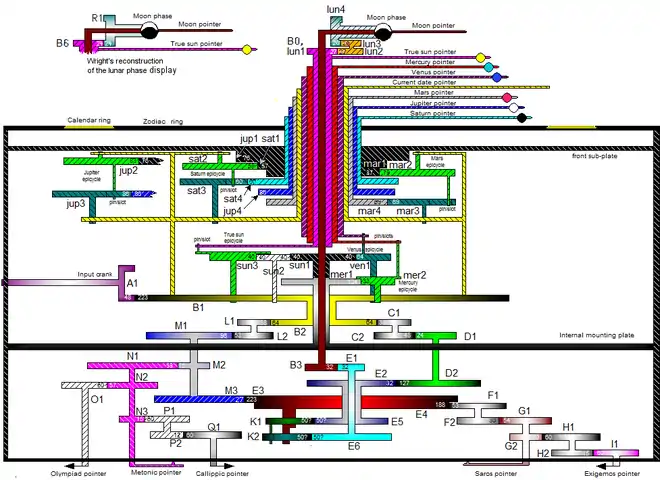
El engrane solar es operado desde la manivela movida manualmente (conectada al engrane a1 que mueve el gran engrane del sol promedio de 4 dientes b1) y mueve por igual al resto de los conjuntos de engranes. El engrane del sol es b1/b2 y b2 tiene 64 dientes. Este mueve directamente el cursor del sol promedio (puede que haya existido un engrane más preciso del sol que representaba la anomalía elíptica del sol; esto se discute más abajo en la reconstrucción de Freeth). En esta discusión, la referencia son móldelos de periodos rotacionales de varios cursores e indicadores; todos asumen que la rotación de b1 es de 360 grados que corresponde con un año tropical, son calculados basados únicamente en la proporción de los engranes mencionados.[5][30][43]
El conjunto de engranes lunar empiezan con el engrane b1 y continúa a través de c1, c2, d1, d2, e2, e5, k1, k2, e6, e1 y b3 hasta llegar al indicador el cara frontal del mecanismo. Los engranes k1 y k2 forman un engrane planetario, son idénticos y no están conectados pero operan “cara a cara” con un perno saliendo de k1 y entrando en una muesca de k2. Ambos engranes tienen diferentes centros de rotación por lo que el perno se mueve hacia adelante y hacia atrás dentro de la muesca, en aumenta y reduce el radio al que opera k2, también varía su velocidad angular (asumiendo que la velocidad de k1 es uniforme) siendo ésta más rápida en ciertas partes. Las velocidades promedio son iguales después de una revolución completa pero la variación de velocidad representa el efecto de la órbita elíptica de la luna como consecuencia de la segunda y tercera ley de Kepler. El periodo rotacional modelado del indicador lunar (promediado de un año) es de 27.321 días, muy cercano al valor moderno de un mes lunar sideral de 27.312661 días. Como se había mencionado antes, la diferencia de los centros de rotación entre k1 y k2 varía el desplazamiento del tiempo del año y el montaje de estos dos engranes en el engrane e3 proporciona un avance precesional del modelado de la elipticidad con un periodo de 8.8826 años, valor similar al valor actual del periodo de precesión lunar de 8.85 años.[5][30][43]
El sistema también modela las fases lunares. El indicador de la luna sostiene un eje a lo largo de sí mismo, sobre este va montado un pequeño eje (r) que se conecta con el indicador del sol en B0 (la conexión entre B0 y el resto de B no es visible en el mecanismo original por lo que se desconoce si B0 es el indicador promedio del sol o un indicador más exacto). El engrane viaja a través del disco con la luna pero también está orientado al sol, este efecto es para realizar una operación diferencial por lo que el engrane gira en el periodo del mes sinódico, midiendo el efecto y e ángulo de diferencia entre los indicadores del sol y la luna. El engrane lleva una pequeña esfera que es visible a través de una abertura en la cara de la luna, está pintado longitudinalmente con una mitad blanca y la otra negra enseñando las fases pictóricamente. Este gira con un periodo de 29.53 días; el valor moderno del mes sinódico es de 29.530589 días.[5][30][43]
El conjunto de engranes metónico está conformado por b1, b2, l1, l2, m1, m2 y n1 (este último está carga el indicador). El periodo rotacional modelado del indicador es de 6939.5 días (a través del espiral de 5 rotaciones) mientras que el valor moderno para el ciclo metónico es de 6939.69 días.[5][30][43]
El conjunto de engranes olímpico se conforma de b1, b2, l1, l2, m1, m2, n1, n2 y 01 (este último está carga el indicador). Su periodo rotacional modelado es de exactamente 4 años como esperado Incidentalmente este es el único cursor del mecanismo que gira en sentido opuesto a las manecillas del reloj, todos los demás giran en dirección opuesta a este.[5][30][43]
El conjunto de engranes calípico se compone de b1, b2, l1, l2, m1, m2, n1, n3, p1, p2 y q1 (este último carga el indicador). Su periodo computacional modelado es de 27,758 días mientras que el valor moderno es de 27,758.8 días.[5][30][43]
El conjunto de engranes de Saros se compone de b1, b2, l1, l2, m1, m3, e3, e4, f1, f2, y g1(este último carga el indicador) y tiene un periodo rotacional modelado del ciclo de Saros de 1643.3 días (esto en 4 rotaciones a lo largo de la pista del espiral); el valor moderno es de 1636.33 días.[5][30][43]
El conjunto de engranes de exeligmos se compone de b1, b2, l1, l2, m1, m3, e3, e4, f1, f2, g1, g2, h1, h2 y i1 (este último carga el indicador). El periodo rotacional modelado de exeligmos es de 19,756 días y el valor moderno es de 19,755.96 días.[5][30][43]
Según parece, los engranes m3, n1-3, p1-2 y q1 no sobrevivieron el naufragio. Las funciones de los indicadores fueron deducidas por los restos de los discos en la cara trasera, y se propuso un engranaje razonable para satisfacer las funciones el cual es generalmente aceptado.[5][30][43]
Esquemas de engranajes propuestos
Debido a que existe un gran espacio entre el indicador promedio del sol y el frente de la cubierta, y al tamaño de funciones mecánicas como el engranaje solar, es muy probable que el mecanismo haya contenido más engranes que se hayan perdido durante o después del naufragio o que fueron eliminados antes de ser cargados al barco.[9] La falta de evidencia y la naturaleza de la parte frontal del mecanismo han llevado a diversos intentos para recrear lo que los griegos de aquel periodo pudieron haber hecho, lo que ha resultado en varias propuestas de soluciones.

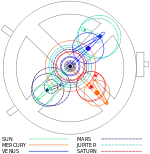
Michael Wright fue la primera persona en diseñar y construir un modelo que no solo contuviera las partes conocidas del mecanismo, este también contaba con la simulación de un potencial sistema planetario. Él sugirió que se habrían hecho más ajustes, además de la anomalía lunar, para la anomalía solar (conocida como la “primera anomalía”). Incluyó indicadores para el sol exacto, Mercurio, Venus, Júpiter y Saturno, todos adicionales a los conocidos indicadores de sol promedio y lunar.[9]
Evans, Carman y Thorndike publicaron una solución con diferencias significantes del modelo de Wright. Su propuesta se basa en la irregularidad espacial de las inscripciones en la cara del disco frontal que ellos observaron, esta irregularidad parecía indicar un indicador solar fuera de centro que simplificaba el mecanismo al eliminar la necesidad de representar la anomalía solar. También sugirieron que en vez de proporcionar indicación planetaria precisa (demostrada imposible por las inscripciones desajustadas) habría discos simples para cada planeta demostrando eventos claves como el ciclo del planeta, apariciones iniciales y finales en el cielo nocturno y cambios de dirección aparentes. Este sistema resultaría en un engranaje general más simple con fuerzas y complejidades reducidas en comparación con el modelo de Wright.[41]
Su propuesta usaba engranajes conectados simples y respondía la incógnita del engrane de 63 dientes en el fragmento D. propusieron el uso de platos con dos caras, una cara con discos separados uniformemente y otra con una brecha encima de la cara para responder ante críticas por la falta de uso del engrane b1. Propusieron que, en vez de usar pilares y soportes para los engranes y los ejes, se usaran iconos climáticos y temporales visibles a través de una ventana.[41]
En un artículo publicado en el año 2012, Carman, Thorndike y Evans propusieron el uso de un sistema de engranaje planetario con seguidores de perno y muesca.[44]
Freeth y Jones publicaron su propuesta en el año 2012 después su extensiva investigación y trabajo. Ellos propusieron una solución compacta y factible la incógnita de la indicación de los planetas. También propusieron la indicación de la anomalía solar (la posición aparente del sol en el disco zodiacal) en un indicador separado del indicador de fecha, que da posición aproximada del sol, al igual que la fecha en el disco mensual, en caso de que los dos discos estuvieran sincronizados correctamente. Su panel frontal era esencialmente el mismo que el de Wright siendo la única diferencia que este modelo no se construyó físicamente sino que es un modelo 3-D de computadora.[9]
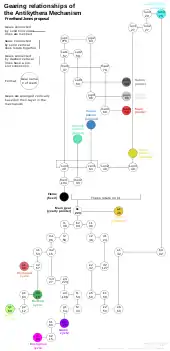
El sistema para sintetizar la anomalía solar es muy similar a la propuesta de Wright. Son 3 engranes fijados al centro del engrane b1 y adjuntos al eje solar, el segundo se fijaba a uno de los rayos (en su propuesta es el inferior izquierdo) actuando como un engrane desocupado y el último engrane se posicionaba junto al anterior y se le equipaba con un perno sobre el cual iría un brazo con una muesca, este brazo se adjuntaba al eje solar induciendo la anomalía según la rueda girara.[9]
El mecanismo planetario inferior incluía al sol (tratado como planeta), a Mercurio y a Venus.[9] Para cada uno de los tres sistemas había un engrane planetario cuyo eje se encontraba montado a b1 resultando en la frecuencia básica siendo un año terrestre (como lo es para el sol y todos los planetas en movimiento epicíclico, a excepción de la luna). Cada uno se conecta con un engrane fijo al cuadro del mecanismo. Cada uno tiene un perno montado, probablemente en una extensión de un lado de un engrane que extiende al mismo pero que no interfiere con los dientes; en algunos casos se necesita cierta distancia entre en centro del engrane y el perno está más lejos que el radio del engrane mismo. Una barra con una muesca a lo largo de sí misma se extiende desde el perno hasta el tubo coaxial adecuado, en cuyo otro extremo se ubica el indicador del objeto al frente de los discos. Las barras podrían ser engranes completos aunque no hay necesidad y sería un desperdicio de material ya que la muesca es la única parte funcional. El uso de las barras previene interferencia entre los tres mecanismos, de los cuales cada uno va en los rayos de la engrane b1. Como resultado hay un nuevo engrane fijo (uno fue identificado en las ruinas y el segundo es compartido por dos planetas), un engrane usado para revertir la dirección de la anomalía solar, tres engranes planetarios y tres barras/tubos coaxiales/indicadores que opcionalmente podrían ser engranes cada uno. Cinco engranes y tres barras muescadas en total.[9]
Los sistemas de los planetas superiores (Marte, Júpiter y Saturno) siguen el principio general del mecanismo de anomalía lunar.[9] Como en el caso de los sistemas inferiores, cada uno tiene un engrane cuyo pivote se encuentra en una extensión de b1 y el cual se conecta con un engrane fijo. Este presenta un perno y un centro de pivote para el engrane planetario, el cual tiene una muesca para el perno, y se conecta con un engrane adjunto a un tubo coaxial y por consiguiente al indicador. Cada uno de los tres mecanismos cabe en un cuadrante de la extensión de b1 por lo que todos están en único plano paralelo con el disco frontal. Cada uno usa un engrane fijo, un engrane conductor, un engrane conducido y un engrane/tubo coaxial o indicador resultando en un total de 12 engranes.
Como resultado se tienen 8 tubos coaxiales de varios tamaños anidados para transferir las rotaciones en el mecanismo a los 8 indicadores. Hay 30 engranes originales, 7 engranes añadidos para completar la funcionalidad del calendario, 17 engranes y 3 barras muescadas para dar soporte a los 6 nuevos indicadores, todo esto resulta en 54 engranes, tres barras y 8 indicadores en el diseño de Freeth y Jones.[9]
En la representación visual, proporcionada por Freeth en la investigación, los indicadores en el disco zodiacal frontal tienen pequeñas piedras redondas identificadoras. Freeth, curiosamente, menciona una cita de un papiro antiguo:
... una voz llega a ti hablando. Deja a las estrellas posicionarse en el tablero de acuerdo con su naturaleza excepto por el Sol y la Luna. Y deja que el Sol sea dorado, la luna plateada, Cronos [Saturno] de obsidiana, Ares [Marte] de ónix rojizo, Afrodita [Venus] lapislázuli vetado de oro, Hermes [Mercurio] turquesa; deja que Zeus [Júpiter] sea de piedra (¿blancuzca?), cristalina (¿?)…[45]
Un nuevo trabajo publicado por Tony Freeth en marzo de 2021[46] afirma haber ideado el primer modelo que se ajusta a todas las pruebas físicas y coincide con las descripciones de las inscripciones científicas grabadas en el mecanismo mismo. El nuevo modelo ha permitido minimizar el número de engranajes de todo el sistema, de modo que encajarían en los espacios reducidos disponibles del dispositivo original. Según el escritor Adam Wocjk, se trata de un avance teórico clave sobre cómo se construyó el mecanismo, cuya factibilidad se pretende demostrar reproduciéndolo con técnicas antiguas.
Precisión
Investigaciones conducidas por Freeth y Jones revelaron que su mecanismo simulado no era particularmente preciso, el indicador de Marte llegaba a estar hasta 38° equivocado. Esto no era debido a errores o imprecisiones en las proporciones de los engranajes, sino que provenían de las propias teorías griegas de aquella época. La precisión no podría ser mejorada hasta que Ptolomeo publicó su Hipótesis Planetaria en la segunda mitad del siglo II d. C. y muy posteriormente con la introducción de la Segunda Ley de Kepler.[9]
«En breve, el mecanismo de Anticitera era una máquina diseñada para predecir acontecimientos siderales basados en las teorías astronómicas sofisticadas más recientes de aquella época, es el único testigo de una historia perdida de brillante ingeniería, un producto de genialidad pura, una de las maravillas del mundo antiguo pero realmente no funcionaba muy bien».[9]
Además de la inexactitud teórica, se encuentra la inexactitud mecánica. Freeth y Jones observaron que el inevitable aflojamiento en el mecanismo a causa de engranajes hechos a mano, con sus dientes triangulares y fricciones entre engranes, y de las superficies de los soportes hubieran abrumado los delicados mecanismos para la corrección solar y lunar del mecanismo.
«A pesar de que la ingeniería es extraordinaria para su época, estudios recientes concluyen que el diseño excedió la precisión de su manufactura por un gran margen, mediante inexactitudes significantes en los engranajes que se acumulaban para cancelar las anomalías sutiles del diseño».[9]
Dispositivos similares en la antigua Grecia
En La República de Marco Tulio Cicerón, un diálogo filosófico del siglo I a. C., se mencionan dos máquinas que algunos autores modernos consideran un tipo de planetario predictor de los movimientos del Sol, la Luna y los cinco planetas conocidos en aquel momento. Construidos ambos por Arquímedes, fueron llevados a Roma por el general Marco Claudio Marcelo tras el asesinato a manos de soldados romanos del gran ingeniero griego en el sitio de Siracusa (212 a. C.), el último bastión de la Magna Grecia (sur de Italia y Sicilia). Marcelo, quien tenía un gran respeto por Arquímedes, se quedó con una de sus máquinas como único botín de su asedio (la segunda la ofreció al templo de Virtus). El dispositivo fue guardado como herencia familiar y Cicerón hizo afirmar a Philus (uno de los personajes del citado diálogo De republica) que Cayo Sulpicio Galo (cónsul con el sobrino de Marcelo en 166 a. C. y acreditado por Plinio el Viejo como el primer romano que escribió un libro explicando los eclipses solares y lunares) daba "explicaciones aprendidas" del mecanismo demostrando su funcionamiento. El diálogo transcurre en una villa perteneciente a Publio Cornelio Escipión Emiliano durante el año 129 a. C., y el texto alusivo es el siguiente:
- He oído a menudo sobre este globo celestial o esfera mencionado acerca de la gran fama de Arquímedes. Su apariencia, aun así, no parecía ser particularmente sorprendente. Hay otro, más elegante en forma y más generalmente conocido, moldeado por el mismo Arquímedes y depositado por el mismo Marcelo en el templo de Virtus en Roma. Pero tan pronto como Galo ha empezado a explicar, con su sublime ciencia, la composición de esta máquina, sentí que el geómetra siciliano debió poseer un genio superior a cualquier cosa que usualmente concibamos perteneciente a nuestra naturaleza. Galo nos aseguró que el sólido y compacto globo era una invención muy antigua y que el primer modelo fue presentado por Tales de Mileto. Que posteriormente Eudoxo de Cnido, un discípulo de Platón, trazó en su superficie las estrellas que aparecen en el cielo y que muchos años después, tomando prestado de Eudoxo este bello diseño y representación, Arato los ilustró en sus versos, no por ninguna ciencia de astronomía sino por el ornamento de la descripción poética. Añadió que la figura de la esfera, que mostraba los movimientos del Sol y la Luna y los cinco planetas o estrellas errantes, no podía ser representados por el globo sólido primitivo. Y que en esto, la invención de Arquímedes fue admirable, porque calculó cómo una simple revolución mantendría desiguales y diversas progresiones en movimientos disimilares.
- Cuando Galo movió este globo mostró la relación de la Luna con el Sol y hubo el mismo número de vueltas en el dispositivo de bronce como el número de días en el verdadero globo del cielo. Así mostró el mismo eclipse del Sol como en el globo [del cielo], al igual que mostró la Luna entrando en el área de sombra de la Tierra cuando el Sol está en línea ... [falta el texto]
- [p.e. mostraba tanto eclipses solares como lunares.][47]
Así pues, al menos una de las máquinas de Arquímedes, probablemente bastante similar al mecanismo de Anticitera, habida cuenta del interés de Galo y de que en esta parte del diálogo De Republica se refieren prodigia astronómicos y en particular eclipses, aún funcionaba alrededor de 150 a. C.
Papo de Alejandría afirmó que Arquímedes escribió un ahora perdido manuscrito sobre la construcción de estos dispositivos titulado Sobre hacer esferas.[48][49] Los textos supervivientes de la biblioteca de Alejandría describen muchas de estas creaciones suyas y algunos contienen croquis simples. Uno de estos dispositivos es su odómetro, el modelo justo que usaron más tarde los romanos para situar su marcador de millas (descrito por Marco Vitruvio, Herón de Alejandría y en el tiempo del emperador Cómodo).[50] Sin embargo, aunque los dibujos en el texto parecen ser funcionales, los intentos de construirlos a semejanza de los mismos han fracasado, pero sí han funcionado cuando los engranajes dibujados (que tienen dientes cuadrados) fueron reemplazados por engranajes del tipo de los que usa el mecanismo de Anticitera, que son en ángulo.[51] Si esto es un ejemplo de los dispositivos creados por Arquímedes y descritos en sus textos perdidos en el incendio de la biblioteca de Alejandría o un dispositivo basado en sus descubrimientos o tiene algo que ver con él es discutible.
Si la cuenta de Cicerón es correcta, esta tecnología existió ya en el siglo III a. C.. El dispositivo de Arquímedes es también mencionado por escritores romanos posteriores como Lactancio (Divinarum Institutionum Libri VII), Claudiano (In sphaeram Archimedes), y Proclo (Comentario en el primer libro de Euclides, Elementos de Geometría) en los siglos IV y V.
Cicerón también dijo que otro de estos dispositivos fue construido recientemente por su amigo Posidonio, "... cada una de las revoluciones de las cuales trae el mismo movimiento en el Sol y la Luna y las cinco estrellas errantes [planetas] como el que es traído cada día y noche en los cielos...".[52]
Es poco probable que alguna de esas máquinas fuera el mecanismo de Anticitera encontrado en el pecio ya que tanto los dispositivos fabricados por Arquímedes y mencionados por Cicerón fueron localizados en Roma al menos 30 años después de la fecha estimada del naufragio y el tercero estuvo casi con certeza en las manos de Posidonio por aquellas fechas. Así que sabemos que hubo al menos cuatro de esos dispositivos. Los científicos modernos que han reconstruido el mecanismo de Anticitera también están de acuerdo en que era demasiado sofisticado para haber sido un dispositivo único.
Esta tecnología fue más tarde, en parte, transmitida a los bizantinos y al mundo islámico, donde dispositivos mecánicos que eran complejos, aunque más simples que el mecanismo de Anticitera, fueron construidos durante la Edad Media.[53] Fragmentos de un calendario mecánico unido a un reloj solar, del siglo V o VI del imperio bizantino han sido encontrados; el calendario pudo haber sido usado para ayudar a contar el tiempo.[54] En el mundo islámico, el libro de Banū Mūsā Kitab al-Hiyal, o Libro de Mecanismos Ingeniosos, fue encargado por el Califa de Bagdad a principios del siglo IX. Este texto describe más de cien dispositivos mecánicos, algunos de los cuales datan de antiguos textos griegos preservados en monasterios. Un calendario mecánico similar al dispositivo bizantino fue descrito por el científico al-Biruni sobre el año 1000, y un astrolabio del siglo XIII, que se conserva, también contiene un dispositivo de relojería similar.[54] Es posible que esta tecnología medieval fuera transmitida a Europa y contribuyera al desarrollo de los relojes mecánicos.[55]
En la cultura popular
La película Indiana Jones y el dial del destino (2023) presenta una trama en torno a una versión ficticia del dispositivo de Anticitera.[56] En la película, el dispositivo se utiliza como un sistema de cartografía temporal que permite predecir grietas temporales para así atravesarlas y viajar en el tiempo. En la película, un científico nazi la busca para viajar al pasado, matar a Hitler y así deshacer los errores que causaron que Alemania perdiera la Segunda Guerra Mundial.
El compositor de música electrónica BT, en su quinto álbum de estudio, This Binary Universe, tituló una canción como «El mecanismo de Antikythera».
Véase también
Referencias
- «The Antikythera Mechanism Research Project». The Antikythera Mechanism Research Project. Archivado desde el original el 21 de febrero de 2011. Consultado el 1 de julio de 2007. «The Antikythera Mechanism is now understood to be dedicated to astronomical phenomena and operates as a complex mechanical 'computer' which tracks the cycles of the Solar System. »
- Seaman, Bill; Rössler, Otto E. (1 de enero de 2011). Neosentience: The Benevolence Engine. Intellect Books. p. 111. ISBN 978-1-84150-404-9. Consultado el 28 de mayo de 2013. «Mike G. Edmunds and colleagues used imaging and high-resolution X-ray tomography to study fragments of the Antikythera Mechanism, a bronze mechanical analog computer thought to calculate astronomical positions ».
- Swedin, Eric G.; Ferro, David L. (24 de octubre de 2007). Computers: The Life Story of a Technology. JHU Press. p. 1. ISBN 978-0-8018-8774-1. Consultado el 28 de mayo de 2013. «It was a mechanical computer for calculating lunar, solar, and stellar calendars. »
- Paphitis, Nicholas (30 de noviembre de 2006). «Experts: Fragments an Ancient Computer». Washington Post. «Imagine tossing a top-notch laptop into the sea, leaving scientists from a foreign culture to scratch their heads over its corroded remains centuries later. A Roman shipmaster inadvertently did something just like it 2,000 years ago off southern Greece, experts said late Thursday. »
- Freeth, Tony; Bitsakis, Yanis; Moussas, Xenophon; Seiradakis, John. H.; Tselikas, A.; Mangou, H.; Zafeiropoulou, M.; Hadland, R. et al. (30 de noviembre de 2006). «Decoding the ancient Greek astronomical calculator known as the Antikythera Mechanism». Nature. 444 Supplement (7119): 587-91. Bibcode:2006Natur.444..587F. PMID 17136087. doi:10.1038/nature05357. Archivado desde el original el 20 de julio de 2015. Consultado el 20 de mayo de 2014.
- Carman, Christián C.; Evans, James (15 de noviembre de 2014). «On the epoch of the Antikythera mechanism and its eclipse predictor». Archive for History of Exact Sciences 68 (6): 693-774. doi:10.1007/s00407-014-0145-5. Consultado el 26 de noviembre de 2014.
- Markoff, John (24 de noviembre de 2014). «On the Trail of an Ancient Mystery - Solving the Riddles of an Early Astronomical Calculator». New York Times. Consultado el 25 de noviembre de 2014.
- Price, Derek de Solla (1974). «Gears from the Greeks. The Antikythera Mechanism: A Calendar Computer from ca. 80 B. C.». Transactions of the American Philosophical Society, New Series 64 (7): 1-70. doi:10.2307/1006146.
- Freeth, Tony; Jones, Alexander (2012). The Cosmos in the Antikythera Mechanism. Institute for the Study of the Ancient World. Consultado el 19 de mayo de 2014.
- Pinotsis, A. D. (30 de agosto de 2007). «The Antikythera mechanism: who was its creator and what was its use and purpose?». Astronomical and Astrophysical Transactions 26. doi:10.1080/10556790601136925. Consultado el 9 de enero de 2015.
- Freeth, Tony; Jones, Alexander; Steele, John M.; Bitsakis, Yanis (31 de julio de 2008). «Calendars with Olympiad display and eclipse prediction on the Antikythera Mechanism». Nature 454 (7204): 614-617. Bibcode:2008Natur.454..614F. PMID 18668103. doi:10.1038/nature07130. Archivado desde el original el 17 de octubre de 2010.
- «Confirman el funcionamiento del mecanismo de Anticitera, la computadora milenaria». La Nación. Consultado el 26 de febrero de 2017.
- «Decoding The Antikythera Mechanism - Investigation of An Ancient Astronomical Calculator». Bibliotecapleyades.net. Consultado el 13 de noviembre de 2012.
- Vetenskapens värld: Bronsklumpen som kan förutsäga framtiden. SVT. 17 October 2012.
- «Mecanismo de Anticitera». eluniversal.com. Consultado el 21 de mayo de 2017.
- «National Archaeological Museum» (en inglés). Archivado desde el original el 24 de marzo de 2016. Consultado el 10 de junio de 2016.
- Marco Tulio Cicerón La República I,21.
- Marchant, Jo (30 de noviembre de 2006). «In search of lost time». Nature 444 (7119): 534-538. Bibcode:2006Natur.444..534M. PMID 17136067. doi:10.1038/444534a. Archivado desde el original el 11 de diciembre de 2013. Consultado el 20 de mayo de 2014.
- Haughton, Brian (26 de diciembre de 2006). Hidden History: Lost Civilizations, Secret Knowledge, and Ancient Mysteries. Career Press. pp. 43-44. ISBN 978-1-56414-897-1. Consultado el 16 de mayo de 2011.
- «Ancient 'computer' starts to yield secrets». Archivado desde el original el 13 de marzo de 2007. Consultado el 23 de marzo de 2007.
- Angelakis, Dimitris G. (2 de mayo de 2005). Quantum Information Processing: From Theory to Experiment. Proceedings of the NATO Advanced Study Institute on Quantum Computation and Quantum Information. Chania, Crete, Greece: IOS Press (publicado el 2006). p. 5. ISBN 978-1-58603-611-9. Consultado el 28 de mayo de 2013. «The Antikythera mechanism, as it is now known, was probably the world's first 'analog computer' – a sophisticated device for calculating the motions of stars and planets. This remarkable assembly of more than 30 gears with a differential... »
- Allen, Martin (27 de mayo de 2007). «Were there others? The Antikythera Mechanism Research Project». Antikythera-mechanism.gr. Archivado desde el original el 21 de julio de 2011. Consultado el 24 de agosto de 2011.
- Антикитерский механизм: сенсация по частям – 2. О чем рассказал расшифрованный текст и будет ли продолжение?
- Lazos, Christos (1994). The Antikythera Computer. ?????S PUBLICATIONS GR.
- «Jacques-Yves Cousteau». Archivado desde el original el 5 de diciembre de 2014. Consultado el 4 de junio de 2015.
- «What was it made of?». Antikythera Mechanism Research Project. 4 de julio de 2007. Archivado desde el original el 18 de abril de 2012. Consultado el 16 de mayo de 2012.
- Freeth, Tony (December 2009). «Decoding an Ancient Computer». Scientific American: 78. Consultado el 26 de noviembre de 2014.
- Article "Pergamum", Columbia Electronic Encyclopedia, 6th Edition, 1.
- Paul Iversen, "The Calendar on the Antikythera Mechanism and the Corinthian Family of Calendars, Hesperia 86 (2017).
- Freeth, Tony; Jones, Alexander; Steele, John M.; Bitsakis, Yanis (31 de julio de 2008). «Calendars with Olympiad display and eclipse prediction on the Antikythera Mechanism». Nature. 454 Supplement (7204): 614-7. Bibcode:2008Natur.454..614F. PMID 18668103. doi:10.1038/nature07130. Archivado desde el original el 27 de septiembre de 2013. Consultado el 20 de mayo de 2014.
- Wright, Michael T. (2007). «The Antikythera Mechanism reconsidered». Interdisciplinary Science Reviews 32 (1): 21-43. doi:10.1179/030801807X163670.
- Freeth, Tony (2006). «Decoding the Antikythera Mechanism: Supplementary Notes 2». Nature 444 (7119): 587-91. Bibcode:2006Natur.444..587F. PMID 17136087. doi:10.1038/nature05357. Archivado desde el original el 26 de enero de 2013. Consultado el 20 de mayo de 2014.
- Антикитерский механизм: сенсация по частям – 3. О мире небесном и подводном
- «The Cosmos on the front of the Antikythera Mechanism». Archivado desde el original el 17 de mayo de 2018. Consultado el 4 de junio de 2015.
- Freeth, T. (2009). «Decoding an Ancient Computer». Scientific American 301 (6): 76-83. PMID 20058643. doi:10.1038/scientificamerican1209-76.
- Anastasiou, Magdalini (2014). Διδακτορική διατριβή: Ο Μηχανισμός των Αντικυθήρων: Αστρονομία και Τεχνολογία στην Αρχαία Ελλάδα (tesis doctoral). Universidad Aristóteles de Tesalónica. pp. 16-19. ISSN 2241-9993. Consultado el 25 de agosto de 2020.
- Wright, Michael T. (March 2006). «The Antikythera Mechanism and the early history of the moon phase display». Antiquarian Horology 29 (3): 319-329. Consultado el 16 de junio de 2014.
- Olmedillas, Joan Carles (2012). Introducción a los sistemas de navegación por satélite. UOC. p. 24. ISBN 978-84-9029-167-2.
- Diego Gustavo Macchi: Descifrando la mecánica del cielo. El mecanismo de Anticitera, p.14, en Revista de tecnología e informática histórica, volumen 2, número 1 (2012).
- «Does it favour a Heliocentric, or Geocentric Universe?». Antikythera Mechanism Research Project. 27 de julio de 2007. Archivado desde el original el 21 de julio de 2011. Consultado el 24 de agosto de 2011.
- Evans, James; Carman, Christián C.; Thorndyke, Alan (February 2010). «Solar anomaly and planetary displays in the Antikythera Mechanism». Journal for the history of astronomy. xli: 1-39. Consultado el 20 de mayo de 2014.
- Wright, Michael T. (June 2005). «The Antikythera Mechanism: a new gearing scheme». Bulletin of the Scientific Instrument Society 85: 2-7.
- «Using Computation to Decode the First Known Computer». IEEE Computer Magazine. 2011-7. July 2011.
- Carman, Christián C.; Thorndyke, Alan; Evans, James (2012). «On the Pin-and-Slot Device of the Antikythera Mechanism, with a New Application to the Superior Planets». Journal for the History of Astronomy 43: 93-116. Bibcode:2012JHA....43...93C. Consultado el 21 de mayo de 2014.
- An extract from a 2nd or 3rd century AD papyrus (P.Wash.Univ.inv. 181+221) about an "Astrologer’s Board", where the astrologer lays out particular stones to represent the Sun, Moon and planets
- Europa Press (13 de marzo de 2021). «Descifran por fin el secreto del mecanismo de Anticitera, el 'ordenador' más antiguo de la historia». 20 minutos. Consultado el 24 de marzo de 2021.
- «M. TVLLI CICERONIS DE RE PVBLICA LIBER PRIMVS». Consultado el 23 de marzo de 2007.
- Rorres, Chris. «Archimedes: Spheres and Planetaria (Introduction)». New York University. Consultado el 27 de marzo de 2011.
- Fildes, Jonathan (29 de noviembre de 2006). «Ancient Moon 'computer' revisited». BBC News. Consultado el 25 de abril de 2010.
- Needham, Volumen 4, Parte 2, 285.
- Andre Sleeswyk, "Vitruvius' odometer", Scientific American, vol. 252, nº 4, pages 188-200 (Octubre de 1981). Ver también: Andre Wegener Sleeswyk, "Vitruvius' waywiser", Archives internationales d'histoire des sciences, vol. 29, páginas 11-22 (1979).
- «Cicero, De Natura Deorum II.88 (or 33-34)». Consultado el 23 de marzo de 2007.
- Archaeology: High tech from Ancient Greece, François Charette, Nature 444, #7119 (30 de noviembre de 2006), pp. 551-552, doi 10.1038/444551a.
- Early mathematical wheelwork: Byzantine calendrical gearing, Francis Maddison, Nature 314 (28 de marzo de 1985), pp. 316–317, doi 10.1038/314316b0.
- In search of lost time, Jo Marchant, Nature 444, #7119 (30 de noviembre de 2006),pp. 534–538,doi 10.1038/444534a
- Grierson, Tim (19 de mayo de 2023). «‘Indiana Jones And The Dial Of Destiny’: Cannes Review». Screen Daily. Consultado el 2 de julio de 2023.
Otras lecturas
Libros
- James, Peter; Thorpe, Nick (1995). Ancient Inventions. New York: Ballantine. ISBN 0-345-40102-6.
- Marchant, Jo (6 de noviembre de 2008). Decoding the Heavens: Solving the Mystery of the World's First Computer. William Heinemann Ltd. ISBN 0-434-01835-X.
- Rosheim, Mark E. (1994). Robot Evolution: The Development of Anthrobotics. John Wiley & Sons. ISBN 0-471-02622-0.
- Russo, Lucio (2004). The Forgotten Revolution: How Science Was Born in 300 BCE and Why It Had To Be Reborn. Berlin: Springer. ISBN 3-540-20396-6.
- Steele, J. M. (2000). Observations and Predictions of Eclipse Times by Early Astronomers. Dordrecht: Kluwer Academic. ISBN 0-7923-6298-5.
- Stephenson, F. R. (1997). Historical Eclipses and the Earth's Rotation. Cambridge, UK: Cambridge Univ. Press. ISBN 0-521-46194-4.
- Toomer, G. J. (1998). Ptolemy's Almagest. Translated by Toomer, G. J. Princeton, New Jersey: Princeton Univ. Press.
Revistas
- Bromley, A. G. (1990). «The Antikythera Mechanism». Horological Journal 132: 412-415.
- Bromley, A. G. (1990). «The Antikythera Mechanism: A Reconstruction». Horological Journal 133 (1): 28-31.
- Bromley, A. G. (1990). «Observations of the Antikythera Mechanism». Antiquarian Horology 18 (6): 641-652.
- Charette, François (2006). «High tech from Ancient Greece». Nature 444 (7119): 551-552. Bibcode:2006Natur.444..551C. PMID 17136077. doi:10.1038/444551a.
- Edmunds, Mike; Morgan, Philip (2000). «The Antikythera Mechanism: Still a Mystery of Greek Astronomy». Astronomy & Geophysics 41 (6): 6-10. Bibcode:2000A&G....41f..10E. doi:10.1046/j.1468-4004.2000.41610.x. (The authors mention that an "extended account" of their researches titled "Computing Aphrodite" is forthcoming in 2001, but it does not seem to have appeared yet.)
- Freeth, T. (2002). «The Antikythera Mechanism: 1. Challenging the Classic Research». Mediterranean Archeology and Archeaometry 2 (1): 21-35.
- Freeth, T. (2002). «The Antikyhera Mechanism: 2. Is it Posidonius' Orrery?». Mediterranean Archeology and Archeaometry 2 (2): 45-58.
- Freeth, T.; Bitsakis, Y.; Moussas, X.; Seiradakis, J. H. et al. (2006). «Decoding the ancient Greek astronomical calculator known as the Antikythera Mechanism». Nature 444 (7119): 587-591. Bibcode:2006Natur.444..587F. PMID 17136087. doi:10.1038/nature05357.
- Freeth, T. (2009). «Decoding an Ancient Computer». Scientific American 301 (6): 76-83. doi:10.1038/scientificamerican1209-76.
- Jones, A. (1991). «The adaptation of Babylonian methods in Greek numerical astronomy». Isis 82 (3): 440-453. doi:10.1086/355836.
- Price, D. de S. (1959). «An Ancient Greek Computer». Scientific American 200 (6): 60-67. doi:10.1038/scientificamerican0659-60.
- Spinellis, Diomidis (May 2008). «The Antikythera Mechanism: A Computer Science Perspective». Computer 41 (5): 22-27. doi:10.1109/MC.2008.166.
- John A. Koulouris,(Esq.) (2008). «The Heavens of Poseidon: The History and Discovery of the AntiKythera Mechanism (In GREEK)». IN NOMINE Portal 1: 1-12.
- Steele, J. M. (2000). «Eclipse prediction in Mesopotamia». Arch. Hist. Exact Sci. 54 (5): 421-454. doi:10.1007/s004070050007.
- Weinberg, G. D.; Grace, V. R.; Edwards, G. R.; Robinson, H. S. et al. (1965). «The Antikythera Shipwreck Reconsidered». Trans Am Philos. Soc. 55 (New Series) (3): 3-48. JSTOR 1005929. doi:10.2307/1005929.
Otros
- Hellenic Ministry of Culture and the National Archaeological Museum, The Anticitera Mechanism Research Project
- Rice, Rob S. (4–7 September 1997). The Antikythera Mechanism: Physical and Intellectual Salvage from the 1st Century BCE. USNA Eleventh Naval History Symposium. Thessaloniki. pp. 19-25.
Enlaces externos
- Diego Gustavo Macchi: Descifrando la mecánica del cielo. El mecanismo de Anticitera, en Revista de tecnología e informática histórica, volumen 2, número 1 (2012).
- The Antikythera Mechanism Research Project (en inglés)
- The Antikythera Mechanism Exhibitions coordinated by the National Hellenic Research Foundation (en inglés)
- Ο Μηχανισμός των Αντικυθήρων libro digital, Academia de Instituciones y Culturas (en griego)(en inglés)
- Jo Marchant, Archimedes and the 2000-year-old computer. New Scientist, 12 de diciembre de 2008 (en inglés)
- Hublot painstakingly recreates a mysterious, 2,100-year-old clockwork relic – but why? (en inglés) Gizmag, 16 de noviembre de 2011 (en inglés)
- 3D model simulator of Price and the Antikythera Mechanism Research Project's representations (en inglés)
- Antikythera Mechanism on the Wolfram Demonstrations Project. (en inglés)
- YAAS - 3D interactive virtual reality simulator in VRML (en inglés)