Metodología de superficie de respuesta
En estadística, la metodología de superficie de respuesta (RSM) explora las relaciones entre varias variables explicativas y una o más variables de respuesta. El método fue introducido por George E. P. Box y K. B. Wilson en 1951. La idea principal de RSM es utilizar una secuencia de experimentos diseñados para obtener una respuesta óptima. Box y Wilson sugieren usar un modelo polinomial de segundo grado para hacer esto. Reconocen que este modelo es solo una aproximación, pero lo usan porque dicho modelo es fácil de estimar y aplicar, incluso cuando se sabe poco sobre el proceso.
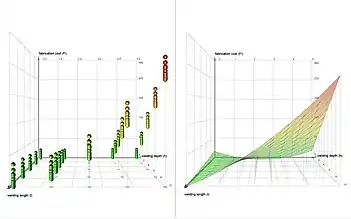
Pueden emplearse enfoques estadísticos como RSM para maximizar la producción de una sustancia especial mediante la optimización de los factores operativos. Últimamente, para la optimización de la formulación, el RSM, que utiliza el diseño adecuado de experimentos (DoE), se ha utilizado ampliamente.[1] A diferencia de los métodos convencionales, la interacción entre las variables del proceso se puede determinar mediante técnicas estadísticas.[2]
Enfoque básico de la metodología de superficie de respuesta
Una forma fácil de estimar un modelo polinomial de primer grado es utilizar un experimento factorial o un diseño factorial fraccional. Esto es suficiente para determinar qué variables explicativas afectan la(s) variable(s) de respuesta de interés. Una vez que se sospecha que solo quedan variables explicativas significativas, se puede implementar un diseño más complicado, como un diseño compuesto central, para estimar un modelo polinomial de segundo grado, que en el mejor de los casos es solo una aproximación. Sin embargo, el modelo de segundo grado se puede utilizar para optimizar (maximizar, minimizar o alcanzar un objetivo específico para) la(s) variable(s) de respuesta de interés.
Propiedades y características importantes de RSM
Ortogonalidad: La propiedad que permite estimar los efectos individuales de los factores k de forma independiente sin (o con un mínimo) de confusión. Además, la ortogonalidad proporciona estimaciones de varianza mínima del coeficiente del modelo para que no estén correlacionadas.
Rotabilidad: La propiedad de rotar puntos del diseño alrededor del centro del espacio factorial. Los momentos de la distribución de los puntos de diseño son constantes.
Uniformidad: Una tercera propiedad de los diseños CCD que se utiliza para controlar el número de puntos centrales es la precisión uniforme.
Geometrías especiales
Cubo
Los diseños cúbicos son discutidos por Kiefer, por Atkinson, Donev y Tobias y por Hardin y Sloane.
Esfera
Los diseños esféricos son discutidos por Kiefer y Hardin y Sloane.
Experimentos de mezcla y geometría simplex
Los experimentos de mezclas se discuten en muchos libros sobre el diseño de experimentos y en los libros de texto de metodología de superficie de respuesta de Box y Draper y de Atkinson, Donev y Tobias. En el libro de texto avanzado de John Cornell aparece una discusión y una encuesta extensas.
Extensiones
Varias funciones objetivas
Algunas extensiones de la metodología de superficie de respuesta se ocupan del problema de respuesta múltiple. Varias variables de respuesta crean dificultades porque lo que es óptimo para una respuesta puede no serlo para otras respuestas. Otras extensiones se utilizan para reducir la variabilidad en una sola respuesta mientras se apunta a un valor específico, o se alcanza un máximo o mínimo cercano al tiempo que se evita que la variabilidad en esa respuesta sea demasiado grande.
Preocupaciones prácticas
La metodología de superficie de respuesta utiliza modelos estadísticos y, por lo tanto, los profesionales deben ser conscientes de que incluso el mejor modelo estadístico es una aproximación a la realidad. En la práctica, tanto los modelos como los valores de los parámetros son desconocidos y están sujetos a incertidumbre además de ignorancia. Por supuesto, un punto óptimo estimado no necesita ser óptimo en realidad, debido a los errores de las estimaciones y a las deficiencias del modelo.
No obstante, la metodología de superficie de respuesta tiene un historial eficaz de ayudar a los investigadores a mejorar productos y servicios: por ejemplo, el modelado de superficie de respuesta original de Box permitió a los ingenieros químicos mejorar un proceso que había estado estancado durante años. Los ingenieros no habían podido permitirse el lujo de ajustar un diseño cúbico de tres niveles para estimar un modelo cuadrático, y sus modelos lineales sesgados estimaron que el gradiente era cero. El diseño de Box redujo los costos de experimentación para que se pudiera ajustar un modelo cuadrático, lo que condujo a una dirección de ascenso (largamente buscada).[3][4]
Véase también
- Diseño Box – Behnken
- Diseño compuesto central
- Kriging mejorado con gradiente (GEK)
- Método IOSO basado en metodología de superficie de respuesta
- Diseños óptimos
- Diseño de Plackett-Burman
- Modelado de funciones polinomiales y racionales
- Regresión polinomial
- Diseño probabilístico
- Modelo sustituto
Referencias
- Karmoker, J.R.; Hasan, I.; Ahmed, N.; Saifuddin, M.; Reza, M.S. (2019). «Development and Optimization of Acyclovir Loaded Mucoadhesive Microspheres by Box -Behnken Design». Dhaka University Journal of Pharmaceutical Sciences 18 (1): 1-12. doi:10.3329/dujps.v18i1.41421.
- Asadi, Nooshin; Zilouei, Hamid (March 2017). «Optimization of organosolv pretreatment of rice straw for enhanced biohydrogen production using Enterobacter aerogenes». Bioresource Technology 227: 335-344. PMID 28042989. doi:10.1016/j.biortech.2016.12.073.
- Box y Wilson, 1951
- Improving Almost Anything: Ideas and Essays, Revised Edition (Wiley Series in Probability and Statistics) George E. P. Box
Otras lecturas
- Box, G.E.P.; Wilson, K.B. (1951). «On the Experimental Attainment of Optimum Conditions». Journal of the Royal Statistical Society: Series B 13 (1): 1-45. doi:10.1111/j.2517-6161.1951.tb00067.x.
- Box, GEP y Draper, Norman. 2007. Superficies de respuesta, mezclas y análisis de crestas, segunda edición [de Empirical Model-Building and Response Surfaces, 1987], Wiley.
- Atkinson, A.C.; Donev, A.N.; Tobias, R.D. (2007). Optimum Experimental Designs, with SAS. Oxford University Press. pp. 511+xvi. ISBN 978-0-19-929660-6.
- Cornell, John (2002). Experiments with Mixtures: Designs, Models, and the Analysis of Mixture Data (third edición). Wiley. ISBN 978-0-471-07916-3.
- Goos, Peter] (2002). The Optimal Design of Blocked and Split-plot Experiments. Lecture Notes in Statistics 164. Springer. ISBN 978-0-387-95515-5.
- Kiefer, Jack Carl (1985). L. D. Brown, ed. Jack Carl Kiefer Collected Papers III Design of Experiments. Springer-Verlag. ISBN 978-0-387-96004-3.
- Pukelsheim, Friedrich (2006). Optimal Design of Experiments. SIAM]. ISBN 978-0-89871-604-7.
- Hardin, R.H.; Sloane, N.J.A. (1993). «A New Approach to the Construction of Optimal Designs». Journal of Statistical Planning and Inference 37 (3): 339-369. doi:10.1016/0378-3758(93)90112-J.
- Hardin, R.H. «Computer-Generated Minimal (and Larger) Response Surface Designs: (I) The Sphere».
- Hardin, R.H. «Computer-Generated Minimal (and Larger) Response Surface Designs: (II) The Cube».
- Ghosh, S.; Rao, C. R., eds. (1996). Design and Analysis of Experiments. Handbook of Statistics 13. North-Holland. ISBN 978-0-444-82061-7.
- Draper, Norman; Lin, Dennis K.J. Response surface designs. pp. 343-375.
- Gaffke, Norbert; Heiligers, Berthold (1996). «30 Approximate designs for polynomial regression: Invariance, admissibility, and optimality». Approximate designs for polynomial regression: Invariance, admissibility, and optimality. Handbook of Statistics 13. pp. 1149-99. ISBN 9780444820617. doi:10.1016/S0169-7161(96)13032-7.
Histórico
- Gergonne, J. D. (1974). «The application of the method of least squares to the interpolation of sequences». Historia Mathematica (Translated by Ralph St. John and S. M. Stigler from the 1815 French edición) 1 (4): 439-447. doi:10.1016/0315-0860(74)90034-2.
- Stigler, Stephen M. (1974). «Gergonne's 1815 paper on the design and analysis of polynomial regression experiments». Historia Mathematica 1 (4): 431-9. doi:10.1016/0315-0860(74)90033-0.
- Peirce, C. S. (1876). «Note on the Theory of the Economy of Research». Coast Survey Report. Appendix No. 14: 197-201. Archivado desde el original el 2 de marzo de 2017. Consultado el 25 de enero de 2021.
- Reimpreso enCollected Papers of Charles Sanders Peirce 7. 1958. párrafos 139 a 157,
- y enPeirce, C. S. (July–August 1967). «Note on the Theory of the Economy of Research». Operations Research 15 (4): 643-8. doi:10.1287/opre.15.4.643. "Nota sobre la teoría de la economía de la investigación". Investigación operativa . 15 (4): 643–8. doi : 10.1287 / opre.15.4.643 . JSTOR 168276 .
- Smith, Kirstine (1918). «On the Standard Deviations of Adjusted and Interpolated Values of an Observed Polynomial Function and its Constants and the Guidance They Give Towards a Proper Choice of the Distribution of the Observations». Biometrika 12 (1/2): 1-85. doi:10.2307/2331929.