Regresión polinomial
En estadística, la regresión polinomial es un modelo de análisis de regresión en el que la relación entre la variable independiente y la variable dependiente se modela con un polinomio de -ésimo grado en . La regresión polinomial se ajusta a una relación no lineal entre el valor de y la media condicional correspondiente de , denotada . Aunque la regresión polinomial ajusta un modelo no lineal a los datos, como problema de estimación estadística es lineal, en el sentido de que la función de regresión es lineal en los parámetros desconocidos que se estiman a partir de los datos. Por esta razón, la regresión polinomial se considera un caso especial de regresión lineal múltiple.
Las variables explicativas (independientes) que resultan de la expansión polinomial de las variables de "línea base" se conocen como términos de grado superior. Estas variables también se utilizan en entornos de clasificación.[1]
Historia
Los modelos de regresión polinomial suelen ajustarse mediante el método de mínimos cuadrados. El método de mínimos cuadrados minimiza la varianza de los estimadores insesgados de los coeficientes, bajo las condiciones del teorema de Gauss-Markov. El método de los mínimos cuadrados fue publicado en 1805 por Legendre y en 1809 por Gauss. El primer diseño de un experimento de regresión polinomial apareció en un artículo de 1815 de Gergonne.[2][3] En el siglo XX, la regresión polinomial jugó un papel importante en el desarrollo del análisis de regresión, con un mayor énfasis en cuestiones de diseño e inferencia.[4] Más recientemente, el uso de modelos polinomiales se ha complementado con otros métodos, y los modelos no polinomiales tienen ventajas para algunas clases de problemas.
Definición y ejemplo
El objetivo del análisis de regresión es modelar el valor esperado de una variable dependiente en términos del valor de una variable independiente (o vector de variables independientes) . En regresión lineal simple, el modelo
se utiliza, donde es un error aleatorio no observado con media cero condicionada a una variable escalar . En este modelo, por cada unidad de aumento en el valor de , la expectativa condicional de aumenta en unidades.
En muchos entornos, esta relación lineal puede no ser válida. Por ejemplo, si estamos modelando el rendimiento de una síntesis química en términos de la temperatura a la que tiene lugar la síntesis, podemos encontrar que el rendimiento mejora al aumentar las cantidades por cada unidad de aumento de temperatura. En este caso, podríamos proponer un modelo cuadrático de la forma
En este modelo, cuando la temperatura aumenta de a unidades, el rendimiento esperado cambia en (Esto se puede ver reemplazando en esta ecuación con y restando la ecuación en de la ecuación en ). Para cambios infinitesimales en , el efecto sobre viene dado por la derivada total con respecto a : El hecho de que el cambio en el rendimiento depende de es lo que hace que la relación entre e no lineal a pesar de que el modelo es lineal en los parámetros a estimar.
En general, podemos modelar el valor esperado de con un polinomio de -ésimo grado, produciendo el modelo de regresión polinómica general
Convenientemente, estos modelos son todos lineales desde el punto de vista de la estimación, ya que la función de regresión es lineal en términos de los parámetros desconocidos Por lo tanto, para el análisis de mínimos cuadrados, los problemas computacionales e inferenciales de la regresión polinomial se pueden abordar por completo utilizando las técnicas de regresión múltiple. Esto se hace tratando , como variables independientes distintas en un modelo de regresión múltiple.
Forma de matriz y cálculo de estimaciones
El modelo de regresión polinomial
se puede expresar en forma de matriz en términos de una matriz diseño , un vector de respuesta , un vector de parámetro y un vector de errores aleatorios. La i-ésima fila de y contendrá el valor e para la muestra de datos i-ésimo. Entonces el modelo se puede escribir como un sistema de ecuaciones lineales:
que cuando se usa la notación matricial pura se escribe como
El vector de coeficientes de regresión polinomial estimados (usando la estimación de mínimos cuadrados ordinarios) es
asumiendo que se requiere para que la matriz sea invertible; entonces desde es una matriz de Vandermonde, se garantiza que la condición de invertibilidad se mantenga si todos los los valores son distintos. Esta es la única solución de mínimos cuadrados.
Interpretación
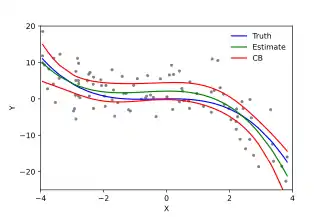
Aunque la regresión polinomial es técnicamente un caso especial de regresión lineal múltiple, la interpretación de un modelo de regresión polinomial ajustado requiere una perspectiva algo diferente. A menudo es difícil interpretar los coeficientes individuales en un ajuste de regresión polinomial, ya que los monomios subyacentes pueden estar altamente correlacionados. Por ejemplo, y tienen una correlación de alrededor de 0,97 cuando se distribuye uniformemente en el intervalo . Aunque la correlación se puede reducir mediante el uso de polinomios ortogonales, generalmente es más informativo considerar la función de regresión ajustada como un todo. A continuación, se pueden utilizar bandas de confianza puntuales o simultáneas para proporcionar una idea de la incertidumbre en la estimación de la función de regresión.
Aproximaciones alternativas
La regresión polinomial es un ejemplo de análisis de regresión que utiliza funciones de base para modelar una relación funcional entre dos cantidades. Más específicamente, reemplaza en regresión lineal con base polinomial , por ejemplo . Un inconveniente de las bases polinomiales es que las funciones base son "no locales", lo que significa que el valor ajustado de y a un valor dado depende en gran medida de los valores de los datos con lejos de .[5] En la estadística moderna, las funciones de base polinomiales se utilizan junto con nuevas funciones de base, como splines, funciones de base radial y ondículas. Estas familias de funciones básicas ofrecen un ajuste más parsimonioso para muchos tipos de datos.
El objetivo de la regresión polinomial es modelar una relación no lineal entre las variables independientes y dependientes (técnicamente, entre la variable independiente y la media condicional de la variable dependiente). Esto es similar al objetivo de la regresión no paramétrica, que tiene como objetivo capturar las relaciones de regresión no lineal. Por lo tanto, los enfoques de regresión no paramétrica, como el suavizado, pueden ser alternativas útiles a la regresión polinomial. Algunos de estos métodos utilizan una forma localizada de regresión polinomial clásica.[6] Una ventaja de la regresión polinomial tradicional es que se puede usar el marco inferencial de regresión múltiple (esto también se aplica cuando se usan otras familias de funciones básicas como splines).
Una última alternativa es utilizar modelos kernelizados como el soporte de regresión vectorial con un kernel polinomial.
Si los residuos tienen una varianza desigual, se puede utilizar un estimador de mínimos cuadrados ponderados para dar cuenta de eso.[7]
Véase también
- Ajuste de curvas
- Regresión lineal
- Regresión polinomial local
- Modelado de funciones polinomiales y racionales
- Interpolación polinomial
- Metodología de superficie de respuesta
Notas
- Microsoft Excel hace uso de la regresión polinomial al ajustar una línea de tendencia a puntos de datos en un gráfico de dispersión X Y.[8]
Referencias
- Chang, Yin-Wen; Hsieh, Cho-Jui; Chang, Kai-Wei; Ringgaard, Michael; Lin, Chih-Jen (2010). «Training and Testing Low-degree Polynomial Data Mappings via Linear SVM». Journal of Machine Learning Research 11 (48): 1471-1490.
- Gergonne, J. D (1 de noviembre de 1974). «The application of the method of least squares to the interpolation of sequences». Historia Mathematica (en inglés) 1 (4): 439-447. ISSN 0315-0860. doi:10.1016/0315-0860(74)90034-2.
- Stigler, Stephen M (1 de noviembre de 1974). «Gergonne's 1815 paper on the design and analysis of polynomial regression experiments». Historia Mathematica (en inglés) 1 (4): 431-439. ISSN 0315-0860. doi:10.1016/0315-0860(74)90033-0.
- Smith, Kirstine (1918). «On the Standard Deviations of Adjusted and Interpolated Values of an Observed Polynomial Function and its Constants and the Guidance They Give Towards a Proper Choice of the Distribution of the Observations». Biometrika 12 (1/2): 1-85. doi:10.2307/2331929.
- Such "non-local" behavior is a property of analytic functions that are not constant (everywhere). Such "non-local" behavior has been widely discussed in statistics:
- Fan, Jianqing (1996). Local Polynomial Modelling and Its Applications: From linear regression to nonlinear regression. Monographs on Statistics and Applied Probability. Chapman & Hall/CRC. ISBN 978-0-412-98321-4.
- Conte, S.D.; De Boor, C. (2018). Elementary Numerical Analysis: An Algorithmic Approach. Classics in Applied Mathematics. Society for Industrial and Applied Mathematics (SIAM, 3600 Market Street, Floor 6, Philadelphia, PA 19104). p. 259. ISBN 978-1-61197-520-8. Consultado el 28 de agosto de 2020.
- Stevenson, Christopher. «Tutorial: Polynomial Regression in Excel». facultystaff.richmond.edu. Consultado el 22 de enero de 2017.
Enlaces externos
- Ajuste de curvas, simulaciones interactivas PhET, Universidad de Colorado en Boulder