Elemento mayorante y minorante

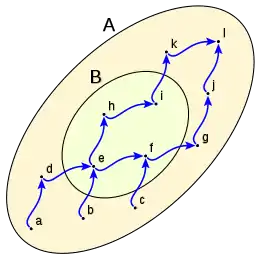
En este ejemplo a, b, d y e son minorantes de B.

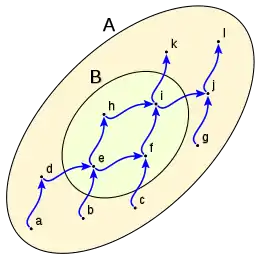
Así dado el conjunto A:

${\displaystyle A=\{a,b,c,d,e,f,g,h,i,j,k,l\}}$

Para el conjunto A en el que se ha definido una relación binaria ${\displaystyle \precsim }$ entre sus elementos, que expresaremos ${\displaystyle (A,\precsim )}$ y siendo x e y elementos de A la relación se representa:

${\displaystyle x\precsim y}$

que se lee: x antecede a y.

Si la relación ${\displaystyle (A,\precsim )}$ cumple las propiedades reflexiva, antisimétrica y transitiva, es por lo tanto es un conjunto parcialmente ordenado.

Si se cumple que:

${\displaystyle x\precsim y\quad \lor \quad y\precsim x}$

el elemento x antecede a y o y antecede a x, se dice que x y y son elementos comparables.

Si se cumple que:

${\displaystyle x\not \precsim y\quad \land \quad y\not \precsim x}$

el elemento x no antecede a y y que y no antecede a x, se dice que x y y son no comparables.

Dado el conjunto B subconjunto de A

${\displaystyle B\subset A}$

${\displaystyle B=\{e,f,h,i\}}$

Los mayorantes de B son todos los elementos de A que son antecedidos por todos los elementos de B, en este caso: i, j, k y l son mayorantes de B.

Entre todos los mayorantes o cotas superiores del conjunto A en el que se ha definido una relación binaria: ${\displaystyle (A,\precsim )}$, siendo este conjunto respecto a la relación binaria un conjunto parcialmente ordenado.

Dado el conjunto B subconjunto de A

${\displaystyle B\subset A}$

Se denomina supremo de B a la menor de estas cotas superiores.

Si, además, el supremo pertenece no sólo al conjunto A sino también a B se denomina máximo de B.

1	2	3	4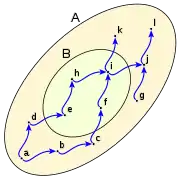
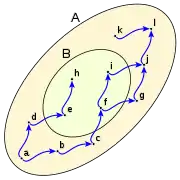
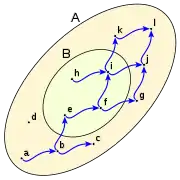
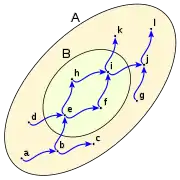
mayorantes: i, j, k, l.	mayorantes: no existe	mayorantes: i, j, k, l.	mayorantes: i, j, k, l.
supremo: i.	supremo: no existe	supremo: i.	supremo: i.
mayor: i.	mayor: no existe	mayor: i.	mayor: i.
minorantes: a.	minorantes: a.	minorantes: no existe	minorantes: a, b, d, e.
ínfimo: a	ínfimo: a.	ínfimo: no existe	ínfimo: e.
menor: no existe	menor: no existe	menor: no existe	menor: e.

• Para el intervalo de números reales (0; 10]: 10 y 11 son mayorantes. 10 sería el supremo del intervalo, y, como además pertenece al mismo, también sería el máximo.
• ${\displaystyle [0_{}^{},+\infty )}$ no tiene mayorante en ${\displaystyle \mathbb {R} }$.

En matemáticas, particularmente en teoría del orden y de conjuntos, el minorante o cota inferior de un subconjunto S de un conjunto parcialmente ordenado P es un elemento de P menor o igual que cualquier elemento de S.

Entre todos los minorantes o cotas inferiores del conjunto P, se denomina ínfimo de S a la mayor de estas cotas inferiores. Si, además el ínfimo pertenece no sólo al conjunto P sino también a S se denomina mínimo de S.

Ejemplo

Así dado el conjunto A:

${\displaystyle A=\{a,b,c,d,e,f,g,h,i,j,k,l\}}$

Para el conjunto A en el que se ha definido una relación binaria ${\displaystyle \precsim }$ entre sus elementos, que expresaremos ${\displaystyle (A,\precsim )}$ y siendo x e y elementos de A la relación se representa:

${\displaystyle x\precsim y}$

que se lee: x antecede a y.

Si la relación ${\displaystyle (A,\precsim )}$ cumple las propiedades reflexiva, antisimétrica y transitiva, es por lo tanto es un conjunto parcialmente ordenado.

Si se cumple que:

${\displaystyle x\precsim y\quad \lor \quad y\precsim x}$

el elemento x antecede a y o y antecede a x, se dice que x y y son elementos comparables.

Si se cumple que:

${\displaystyle x\not \precsim y\quad \land \quad y\not \precsim x}$

el elemento x no antecede a y y que y no antecede a x, se dice que x y y son no comparables.

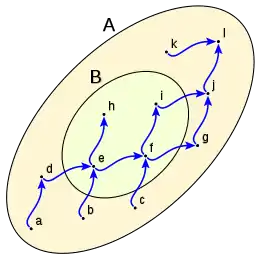
Dado el conjunto B subconjunto de A

${\displaystyle B\subset A}$

${\displaystyle B=\{e,f,h,i\}}$

Los minorante de B son todos los elementos de A que anteceden a todos los elementos de B, en este caso: a, b, d y e son minorantes de B

En el ejemplo c no es minorante de B al ser no comparable con e ni con h.

• Para el intervalo de números reales (0 ; 10]: 0 y -7 son minorantes. 0 sería el ínfimo, pero como no pertenece al intervalo, no sería mínimo del intervalo.
• Para este otro intervalo de números reales ${\displaystyle [0_{}^{},+\infty )}$ -5 y -23 son minorantes, mientras que 0 es su ínfimo y también el mínimo ya que pertenece al intervalo.

Refiere a la propiedad que cumple cierto valor dentro de un conjunto/lista L de valores ordenados. Como ejemplo se encuentra esta definición aplicada a la solución del problema The Playboy Chimp para dar usa solución eficiente en tiempo.

Dado un elemento C que puede o no pertenecer a dicho conjunto. x es cualquier valor de dicho conjunto que puede ser igual a C.

Lower bound: El mayor valor de C que es estrictamente menor. (∃x |x ∈ L: x < C )

Upper bound: El menor valor de C que es estrictamente mayor. (∃x |x ∈ L: x > C )

Implementación en Python

def lower_bound(a, c):
    #Inferior (Izq) el mas grande de los pequeños
    ans = -1
    if a[0] >= c: ans = -1
    else:
        low, hi = 0, len(a)
        while low+1 != hi:
            mid = low + ((hi-low)//2)
            if a[mid] < c:  low = mid
            else: 
                hi = mid
            ans = low   
    return ans

def upper_bound(a, c):
    #superior (Der)  el mas pequeño de los grandes
    ans = -1    
    if a[len(a)-1] <= c: ans = -1
    else:        
        low, hi = 0, len(a)        
        while low+1 != hi:  
            mid = low + ((hi-low)//2)
            if a[mid-1] > c:  hi = mid
            else: 
                low = mid
            ans = low     
    return ans

# El algoritmo retorna el indice que cumple con la definición.
# si retorna -1.. el valor no se puede encontrar en a ; a es una lista ordenada ascendentemente  de números natural.
# Se llama así: print( down_bound(L, c), upper_bound(L, c) )

Cada resultado en Down bound y en Upper bound es el correspondiente al valor en C. C es una lista de números.

L = [2,3,5,7,12,15]  ; L es una lista de números naturales

Valor de C = {1,2,3,5,12,15,16,100}

Down bound = {-1, -1, 0, 1, 3, 4, 5, 5}

Upper bound = {0, 1, 2, 3, 5, -1, -1, -1}

• Acotado

• Elemento maximal y minimal
• Elemento máximo y mínimo

• Elemento mayorante y minorante
• Elemento mayor y menor

• Elemento supremo e ínfimo

• Birkhoff, Garrett (1967). Lattice Theory (en inglés) (2da edición). Estados Unidos: American Mathematical Society, Colloquium Publications. pp. 423. ISBN 0-8218-1025-1. ISSN 0065-9258. Consultado el 21 de noviembre de 2010. (requiere registro).