Modelo de crecimiento poblacional
Un modelo de población o modelo poblacional es un tipo de modelo matemático que se aplica al estudio de la dinámica de poblaciones.
Fundamentos
Los modelos permiten una mejor comprensión de cómo funcionan las interacciones y procesos complejos. El modelado de interacciones dinámicas en la naturaleza puede proporcionar una forma manejable de comprender cómo los números cambian con el tiempo o en relación entre sí. Se pueden notar muchos patrones usando el modelado de población como herramienta.[1]
El modelado ecológico de la población se refiere a los cambios en parámetros tales como el tamaño de la población y la distribución por edades dentro de una población. Esto podría deberse a interacciones con el medio ambiente, individuos de su propia especie u otras especies. Los modelos de población se utilizan para determinar la cosecha máxima para los agricultores, para comprender la dinámica de las invasiones biológicas y para la conservación del medio ambiente. Los modelos de población también se utilizan para comprender la propagación de parásitos, virus y enfermedades.[2]
Otra forma en que los modelos de poblaciones son útiles es cuando las especies se ponen en peligro. Los modelos de población pueden rastrear las especies frágiles y trabajar y frenar el declive.
Historia
Los biólogos de fines del siglo XVIII comenzaron a desarrollar técnicas en el modelado de poblaciones para comprender la dinámica del crecimiento y la reducción de todas las poblaciones de organismos vivos. Thomas Malthus fue uno de los primeros en notar que las poblaciones crecieron con un patrón geométrico mientras contemplaban el destino de la humanidad.[3] Uno de los modelos más básicos e importantes de crecimiento de la población fue el modelo logístico de crecimiento de la población formulado por Pierre François Verhulst en 1838. El modelo logístico toma la forma de una curva sigmoidea y describe el crecimiento de una población como exponencial, seguido de una disminución en el crecimiento y limitado por una capacidad de carga debido a las presiones ambientales.[4]
El modelado de la población se convirtió en un interés particular para los biólogos en el siglo XX cuando un biólogo como Raymond Pearl notó la presión sobre medios limitados de sustento debido al aumento de las poblaciones humanas en algunas partes de Europa. En 1921, Pearl invitó al físico Alfred J. Lotka para que lo ayudara en su laboratorio. Lotka desarrolló ecuaciones diferenciales emparejadas que mostraban el efecto de un parásito en su presa. El matemático Vito Volterra equiparó la relación entre dos especies independientes de Lotka. Juntos, Lotka y Volterra formaron el modelo de competencia Lotka-Volterra que aplica la ecuación logística a dos especies que ilustran las interacciones de competencia, depredación y parasitismo entre especies.[3] En 1939, Patrick Leslie hizo contribuciones al modelado de la población cuando comenzó a trabajar en biomatemática. Leslie enfatizó la importancia de construir una tabla de vida para comprender el efecto que las estrategias clave de historia de vida jugaron en la dinámica de poblaciones enteras. El álgebra matricial fue utilizado por Leslie junto con tablas de vida para extender el trabajo de Lotka.[5] Los modelos matriciales de poblaciones calculan el crecimiento de una población con variables de historia de vida. Más tarde, Robert MacArthur y EO Wilson caracterizaron la biogeografía de islas. El modelo de equilibrio de la biogeografía de la isla describe el número de especies en una isla como un equilibrio de inmigración y extinción. El modelo de población logística, el modelo de ecología comunitaria Lotka-Volterra, el modelo de matriz de tabla de vida, el modelo de equilibrio de la biogeografía de islas y sus variaciones son la base para el modelo de población ecológica actual.[6]
Modelos
Modelo de Malthus
Malthus afirmaba que la velocidad de crecimiento con respecto a la población crecía en progresión geométrica, es decir, la tasa de crecimiento es constante. Así, si llamamos P(t) al número de individuos existentes en el tiempo t, se lo representa en la siguiente forma:
Resolviendo la ecuación lineal se obtiene
donde
- P0 = P(0) es el tamaño inicial de la población,
- r = la tasa de crecimiento de la población
- t = tiempo.
El modelo también se puede escribir en forma de ecuación diferencial:
El modelo de Malthus tiene distintas aplicaciones dependiendo del signo de a. Cuando es positiva se usa en la teoría de poblaciones y economía. Si a < 0, se utiliza para calcular la vida media o semivida de un fármaco. Este modelo también está asociado a problemas de desintegración radiactiva.
Ejemplos de modelos individuales

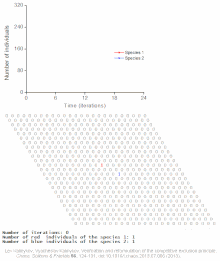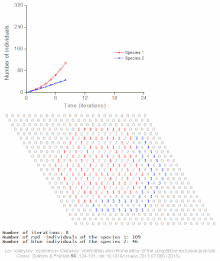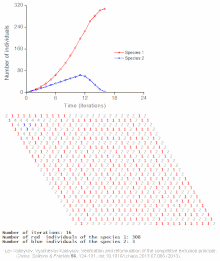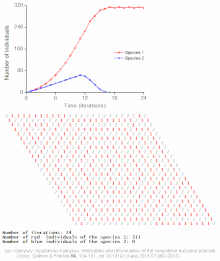
Véase también
Referencias
- Worster, Donald (1994). Nature's Economy. Cambridge University Press. pp. 398–401.
- Uyenoyama, Marcy (2004). Rama Singh, ed. The Evolution of Population Biology. Cambridge University Press. pp. 1–19.
- McIntosh, Robert (1985). The Background of Ecology. Cambridge University Press. pp. 171-198.
- Renshaw, Eric (1991). Modeling Biological Populations in Space and Time. Cambridge University Press. pp. 6-9.
- Kingsland, Sharon (1995). Modeling Nature: Episodes in the History of Population Ecology. University of Chicago Press. pp. 127-146.
- Gotelli, Nicholas (2001). A Primer of Ecology. Sinauer.
Enlaces externos
- Red de código compartido GreenBoxes . Greenboxes (Beta) es un repositorio de código de modelado de población de código abierto. Greenboxes permite a los usuarios una manera fácil de compartir su código y buscar otros códigos compartidos.