Muestreo de hipercubo latino
El muestreo de hipercubo latino (también conocido como LHS, de las iniciales de su nombre en inglés, "latin hypercube sampling") es un método estadístico para generar una muestra casi aleatoria de valores de parámetros a partir de una distribución conjunta. Los métodos de muestreo se utilizan a menudo para diseñar experimentos computarizados o para la integración de Montecarlo.
El método fue descrito por Michael McKay del Laboratorio Nacional de Los Álamos en 1979.[1] Una técnica equivalente independiente fue propuesta por Eglājs en 1977.[2] Fue desarrollada por Ronald L. Iman y sus coautores en 1981.[3] Más adelante se publicaron códigos y manuales informáticos detallados.[4]
En el contexto del muestreo estadístico, una cuadrícula que contiene posiciones de muestra es un cuadrado latino si (y solo si) hay solo una muestra en cada fila y en cada columna. Un hipercubo latino es la generalización de este concepto a un número arbitrario de dimensiones, por lo que cada muestra es la única en cada hiperplano alineado al eje que lo contiene.
Cuando se muestrea una función de variables, el rango de cada variable se divide en intervalos igualmente probables. A continuación, se colocan los puntos de muestra para satisfacer los requisitos del hipercubo latino; esto obliga a que el número de divisiones, , sea igual para cada variable. Este esquema de muestreo no requiere más muestras para más dimensiones (variables); esta independencia es una de las principales ventajas de este esquema de muestreo. Otra ventaja es que se pueden tomar muestras aleatorias una cada vez, recordando qué muestras se tomaron hasta el momento.
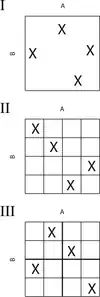
En dos dimensiones, la diferencia entre muestreo aleatorio, muestreo de hipercubo latino y muestreo ortogonal se puede explicar de la siguiente manera:
- En un muestreo aleatorio se generan nuevos puntos de muestra sin tener en cuenta los puntos de muestra generados previamente. No es necesario saber de antemano cuántos puntos de muestra se necesitan.
- En un muestreo de hipercubo latino primero se debe decidir cuántos puntos de muestra usar y para cada punto de muestra recordar en qué fila y columna se tomó el punto de muestra. Tal configuración es similar a tener N torres en un tablero de ajedrez sin amenazarse entre sí.
- En un muestreo ortogonal, el espacio muestral se divide en subespacios igualmente probables. Luego, todos los puntos de muestra se eligen simultáneamente, asegurándose de que el conjunto total de puntos de muestra sea una muestra de hipercubo latino y de que cada subespacio se muestree con la misma densidad.
Por lo tanto, el muestreo ortogonal asegura que el conjunto de números aleatorios es un muy buen representante de la variabilidad real, el método del hipercubo latino asegura que el conjunto de números aleatorios es representativo de la variabilidad real, mientras que el muestreo aleatorio tradicional (a veces llamado de fuerza bruta) es solo un conjunto de números aleatorios sin garantías.
Referencias
- McKay, M.D.; Beckman, R.J.; Conover, W.J. (May 1979). «A Comparison of Three Methods for Selecting Values of Input Variables in the Analysis of Output from a Computer Code». Technometrics (American Statistical Association) 21 (2): 239-245. ISSN 0040-1706. JSTOR 1268522. OSTI 5236110. doi:10.2307/1268522.
- Eglajs, V.; Audze P. (1977). «New approach to the design of multifactor experiments». Problems of Dynamics and Strengths. 35 (en russian) (Riga: Zinatne Publishing House): 104-107.
- Iman, R.L.; Helton, J.C.; Campbell, J.E. (1981). «An approach to sensitivity analysis of computer models, Part 1. Introduction, input variable selection and preliminary variable assessment». Journal of Quality Technology 13 (3): 174-183. doi:10.1080/00224065.1981.11978748.
- Iman, R.L.; Davenport, J.M.; Zeigler, D.K. (1980). Latin hypercube sampling (program user's guide). OSTI 5571631.
Lecturas relacionadas
- Tang, B. (1993). «Orthogonal Array-Based Latin Hypercubes». Journal of the American Statistical Association 88 (424): 1392-1397. JSTOR 2291282. doi:10.2307/2291282.
- Owen, A.B. (1992). «Orthogonal arrays for computer experiments, integration and visualization». Statistica Sinica 2: 439-452.
- Ye, K.Q. (1998). «Orthogonal column Latin hypercubes and their application in computer experiments». Journal of the American Statistical Association 93 (444): 1430-1439. JSTOR 2670057. doi:10.2307/2670057.