Cota superior asintótica
En análisis de algoritmos, una cota superior asintótica es una función que sirve de cota superior de otra función cuando el argumento tiende a infinito. Usualmente se utiliza la notación de Landau: O(g(x)), Orden de g(x), coloquialmente llamada Notación O Grande, para referirse a las funciones acotadas superiormente por la función g(x).
Formalmente se define:
Una función f(x) pertenece a O(g(x)) cuando existe una constante positiva c tal que a partir de un valor , f(x) no sobrepasa a . Quiere decir que la función f es inferior a g a partir de un valor dado salvo por un factor constante.
La cota superior asintótica tiene gran importancia en la Teoría de la complejidad computacional cuando se definen las clases de complejidad.
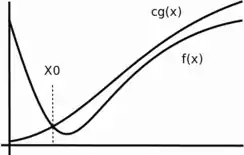
A pesar de que O(g(x)) está definida como un conjunto, se acostumbra escribir f(x)=O(g(x)) en lugar de f(x)∈O(g(x)), ya que la clase de equivalencia de f coincide con el conjunto O(g(x). Muchas veces también se habla de la función nombrando únicamente su expresión, como en x² en lugar de h(x)=x², siempre que esté claro cuál es el parámetro de la función dentro de la expresión. En la gráfica se da un ejemplo esquemático de cómo se comporta con respecto a f(x) cuando x tiende a infinito. Nótese además que dicho conjunto es no vacío pues g(x)=O(g(x)).
La cota ajustada asintótica (notación Θ) tiene relación con las cotas asintóticas superior e inferior (notación Ω):
Propiedades
Sea , sean , Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): {\displaystyle g_1:E\to \mathbb{R}} , , funciones y un real. Entonces los siguientes enunciados son ciertos:
- i) Si y , entonces
- ii) Si y ,entonces
- iii) (aquí es igualdad entre conjuntos)
- iv) Si y , entonces
- v) Si entonces (aquí es igualdad entre conjuntos)
- vi) Si , entonces .
Ejemplos
- La función f(x) = x+10 puede ser acotada superiormente por la función g(x) = x². Para demostrarlo basta notar que para todo valor de x ≥ 3.7016, se cumple x+10 ≤ x². Por tanto x+10 = O(x²). Sin embargo, x² no sirve como cota inferior para x+10, es decir, .
Observación: Este ejemplo muestra que no implica , es decir, la relación entre funciones dada por la notación de Landau no es simétrica. Sin embargo, sí es reflexiva: - La función 200x está acotada superiormente por x². Quiere decir que cuando x tiende a infinito el valor de 200x se puede despreciar con respecto al de x².
Órdenes usuales para funciones
Los órdenes más utilizados en análisis de algoritmos, en orden creciente, son los siguientes (donde c representa una constante y n el tamaño de la entrada):
| notación | nombre |
|---|---|
| O(1) | orden constante |
| O(log log n) | orden sublogarítmica |
| O(log n) | orden logarítmica |
| O() | orden sublineal |
| O(n) | orden lineal o de primer orden |
| O(n · log n) | orden lineal logarítmica |
| O(n2) | orden cuadrática o de segundo orden |
| O(n3), ... | orden cúbica o de tercer orden, ... |
| O(nc) | orden potencial fija |
| O(cn), n > 1 | orden exponencial |
| O(n!) | orden factorial |
| O(nn) | orden potencial exponencial |
Bibliografía
- Introduction to Algorithms, Second Edition by Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein