Operaciones booleanas sobre polígonos

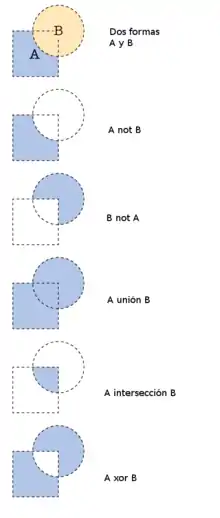
En computación gráfica, las operaciones booleanas sobre polígonos (conjunción, disyunción, complemento, o exclusivo, etc.) operan sobre uno o más conjuntos de polígonos. Estos conjuntos de operaciones son ampliamente utilizados en la generación de gráficos por computadora, CAD, y en EDA (en el diseño y verificación de circuitos integrados).

Principales operaciones booleanas

Algoritmos

Usos en software

Los primeros algoritmos para realizar las operaciones booleanas sobre polígonos se basaban en el uso de bitmaps. Utilizar bitmaps para modelar formas de polígonos tiene muchas desventajas. Una de ellas es el alto consumo de memoria debido a que la resolución del polígono es proporcional al número de bits utilizados para representar los polígonos. Mientras más alta sea la resolución deseada, mayor es el número de bits requeridos.

Las implementaciones modernas de las operaciones booleanas sobre polígonos tienden a utilizar algoritmos de barrido de planos (o algoritmos de barrido de líneas).

Las operaciones booleanas sobre polígonos convexos y los polígonos monótonos de misma dirección pueden ser realizados en tiempo lineal.[1]

Véase también

Geometría sólida constructiva, un método para definir formas tridimensionales que utilizan un conjunto similar de operaciones.

Referencias

Katz, Matthew J.; Overmars, Mark H.; Sharir, Micha (1992). «Efficient hidden surface removal for objects with small union size». Computational Geometry: Theory and Applications 2 (4): 223-234. doi:10.1016/0925-7721(92)90024-M..

Enlaces externos

Páginas de Geometría computacional en UIUC
Geometría planar constructiva, por Dave Eberly.
Comparación de operaciones de recorte de polígonos por Michael Leonov

Datos: Q4943361

Este artículo ha sido escrito por Wikipedia. El texto está disponible bajo la licencia Creative Commons - Atribución - CompartirIgual. Pueden aplicarse cláusulas adicionales a los archivos multimedia.

[1] Katz, Matthew J.; Overmars, Mark H.; Sharir, Micha (1992). «Efficient hidden surface removal for objects with small union size». Computational Geometry: Theory and Applications 2 (4): 223-234. doi:10.1016/0925-7721(92)90024-M..