Oscilador (autómata celular)
En un autómata celular, un oscilador es un patrón que regresa a su estado original, en la misma orientación y posición, después de un número finito de generaciones. Por tanto, la evolución de este tipo de patrón hace que se repita de forma indefinida. Dependiendo del contexto, el término podría también incluir a las naves espaciales.
El menor número de generaciones necesario antes de que un patrón regrese a su estado inicial es conocido como el periodo del oscilador. A un oscilador con un periodo de una sola generación se le conoce como vida estática, ya que dicho patrón nunca cambia. En ocasiones, no se considera que las vidas estáticas sean osciladores. Otra condición común es que un oscilador debe ser finito.
Ejemplos
En el Juego de la vida de Conway, se conocen osciladores finitos para prácticamente cualquier periodo. Las excepciones son 19, 23, 38, 41, 43 y 53. Pese a que no se sabe a ciencia cierta si existen osciladores para dichos periodos, hay firmas creencias de que debe haberlos.
Además, aunque existen osciladores de periodo 34, los únicos ejemplos conocidos se consideran triviales porque consisten esencialmente en componentes separados que oscilan durante periodos menores. Por ejemplo, se puede crear un oscilador de periodo 34 situando osciladores de periodo 2 y de periodo 17 que no interaccionen entre sí, con lo que el periodo del conjunto correspondería al mínimo común múltiplo de dichos periodos. Se considera que un oscilador no es trivial si contiene al menos una célula que oscile con el periodo necesitado.
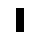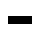 Parpadeador, periodo 2
Parpadeador, periodo 2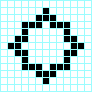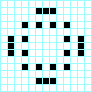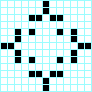 Estrella, periodo 3
Estrella, periodo 3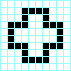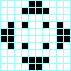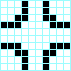 Cruz, periodo 3
Cruz, periodo 3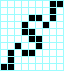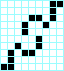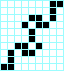 Beso con lengua, periodo 3
Beso con lengua, periodo 3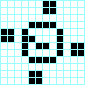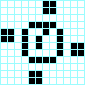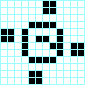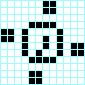 Reloj, periodo 4
Reloj, periodo 4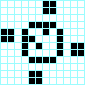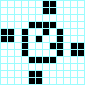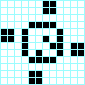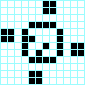 Molinillo, periodo 4
Molinillo, periodo 4 Octógono, periodo 5
Octógono, periodo 5 Fumarola, periodo 5
Fumarola, periodo 5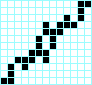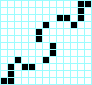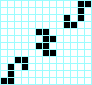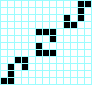 Pentoad, periodo 5
Pentoad, periodo 5 Galaxia de Kok, periodo 8
Galaxia de Kok, periodo 8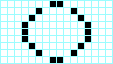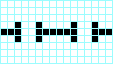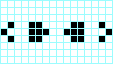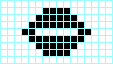 Pentadecathlon, periodo 15
Pentadecathlon, periodo 15
Enlaces externos
- Life wiki:Lista de osciladores conocidos