Polígono funicular

El polígono funicular es un procedimiento gráfico para el cálculo de reacciones y fuerza resultante a partir de un conjunto de fuerzas coplanares. El nombre procede del latín funiculum (cordel, cuerda pequeña) y se refiere al hecho de que el polígono funicular de un sistema de fuerzas sería precisamente la forma que adoptaría un cordel sometido a dicho sistema de fuerzas. Cuando las fuerzas son exclusivamente el peso propio del cordel, se trata de una catenaria.

Descripción

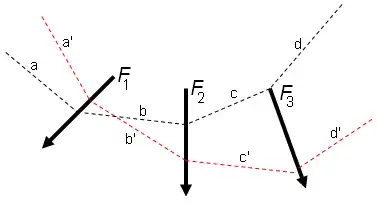
Un sistema de tres fuerzas y dos polígonos funiculares diferentes abcd en negro y a'b'c'd' en rojo, para dicho sistema de fuerzas. Su construcción se aclara en la siguiente sección.

Dado un conjunto de fuerzas en el plano, un polígono funicular para ese sistema de fuerzas es una línea poligonal (no necesariamente cerrada) cuyos vértices recaen sobre las líneas de acción de las fuerzas y los ángulos que forma en cada vértice dependen de la magnitud de la fuerza.

Cabe destacar que el polígono funicular no es único, sino que para un conjunto de fuerzas pueden dibujarse muchos polígonos funiculares que cumplan las condiciones anteriores. Intuitivamente, esto se puede justificar a partir de la idea de que el polígono funicular sería la forma adoptada por una cuerda inextensible ideal sin masa sometida a esas fuerzas. Inicialmente se puede colocar según una dirección arbitraria en el plano y a medida que se deja que las fuerzas actúen sobre ella se genera el polígono funicular. Dos cuerdas idénticas pero en orientaciones originales diferentes generarán polígonos funiculares distintos, aunque relacionados geométricamente.

Procedimiento

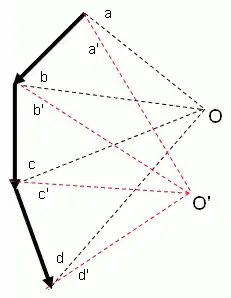
Las tres fuerzas de la sección anterior y los dos polos usados para trazar los dos polígonos funiculares abcd (negro) y a'b'c'd' (rojo).

Dado un sistema finito de fuerzas de n coplanares el polígono funicular consta de n+1 lados, para encontrar la fuerza resultante se dibuja un diagrama de fuerzas. Pasos a seguir:

Se selecciona un punto arbitrario del diagrama de fuerzas llamado polo O.
Se trazan los llamados radios polares que unen los extremos de las fuerzas con el punto O. Al existir n fuerzas existirán n+1 extremos y por tanto el mismo número de radios polares.
Se toma el primero de los radios polares y se dibuja una semirrecta paralela al mismo que interseque con la recta de acción de la primera fuerza.
Se consideran el segundo, tercero, ..., n-ésimo radio polar y se dibujan segmentos paralelos entre las rectas de acción de las fuerzas originales, uno a continuación de otro.
Se toma en (n+1)-ésimo radio polar y se dibuja una semirecta empezando desde el extremo del último segmento dibujado.

Así los n+1 radios polares del diagrama de fuerzas constituyen una línea polígonal continua, que es precisamente el polígono funicular asociado a la elección del polo O. Nótese que si se toma un polo diferente O' y se repite el procedimiento de 5 pasos anterior se obtiene un polígono funicular diferente, pero que es igualmente válido para calcular el punto de paso de la resultante.

Propiedades

Dado un sistema de fuerzas el polígono funicular está en una de estas situaciones:

El polígono funicular es abierto, en cuyo caso el sistema de fuerzas es estáticamente equivalente a una única fuerza resultante.
El polígono funicular es cerrado siendo el primer y último lado paralelos aunque no coincidentes, en ese caso, la fuerza resultante es cero y el sistema de fuerzas equivale a un par.
El polígono funicular es cerrado siendo el primer y último lado coincidentes, en ese caso, la fuerza resultante y el momento resultante son nulos con lo cual el sistema de fuerzas original está en equilibrio mecánico.

Aplicaciones

El polígono funicular puede emplearse para algunas operaciones elementales de la estática gráfica como determinar un punto de paso de la fuerza resultante de un conjunto de fuerzas, para determinar alguna reacción o fuerza incógnita en un conjunto de fuerzas en equilibrio.

También puede ser usado para operaciones más complejas como la determinación de la forma ideal de un arco o estructura porticada que garantiza que todos los tramos del mismo trabajen en compresión. Esta condición es muy importante cuando se construyen estructuras mediante bloques de piedra o mampostería. Y puede resultar también incluso en estructuras de hormigón armado con el fin de aprovechar la máxima capacidad del hormigón en compresión.

Cálculo de la resultante

Nótese que dado un sistema de fuerzas coplanares $\{\mathbf {F} _{1},\mathbf {F} _{2},\cdots ,\mathbf {F} _{n}\}$ con puntos de aplicación diferentes $\{P_{1},P_{2},\cdots ,P_{n}\}$ , se llamará fuerza resultante a una fuerza:

$\mathbf {F} _{R}=\mathbf {F} _{1}+\mathbf {F} _{2}+\cdots +\mathbf {F} _{n}$

Cuya recta de acción pasa por el punto adecuado. Para determinar la recta de paso $P_{R}\,$ , o equivalentemente un punto de paso, de dicha recta se usa el polígono funicular. Más concretamente se dibuja un polígono funicular cualquiera para el sistema de fuerzas y se prologan las dos semirectas extremas de dicho polígono funicular obteniéndose un punto de corte. La existencia de dicho punto de corte está garantizada siempre y cuando la resultante sea diferente de cero. Ese punto de corte es pertenece a la recta de acción de la fuerza resultante y por tanto queda resuelto el problema de situar la fuerza resultante en el lugar adecuado.

Cálculo de reacciones

Dado un sistema isostático en equilibrio en el que actúan sólo dos reacciones R_A y R_B, de las que se conocen los puntos de aplicación P_A y P_B de las mismas y la dirección de una de ellas. Puede usarse el método del polígono funicular para encontrar gráficamente el valor de dichas reacciones. Para ello se aplica la propiedad evidente de que un sistema de tres fuerzas en equilibrio deben ser concurrentes en un punto y a continuación se siguen estos pasos:

Se calcula mediante el polígono funicular la recta de acción de la resultante F_R, tal como se explicó en el apartado anterior.
Se busca la recta de acción de la reacción de dirección conocida (supongamos sin pérdida de generalidad que esta es la que se llamó R_A), y se busca se intersección P_in con la recta de acción de la resultante.
Se une el punto de paso de la otra reacción (es decir, R_B) con el punto encontrado anteriormente y se traza una recta, es decir, se busca la recta que pasa por P_in y P_B. Esta recta tendrá la dirección de la reacción R_B.
Conocidos ahora las direcciones de R_A, R_B y F_R basta construir un triángulo orientado de lados paralelos a las tres direcciones anteriores. A partir de las longitudes de los lados del triángulo pueden deducirse trivialmente el valor de las reacciones.

Referencias

Bibliografía

Timoshenko & Young: Teoría de las estructuras, Ed. Urmo, 1981, ISBN 978-84-314-0241-9.

Datos: Q3333656

Este artículo ha sido escrito por Wikipedia. El texto está disponible bajo la licencia Creative Commons - Atribución - CompartirIgual. Pueden aplicarse cláusulas adicionales a los archivos multimedia.