Poliedro de Goldberg

En matemáticas, y más específicamente en combinatoria poliédrica, un poliedro de Goldberg es un politopo convexo cuyas caras son hexágonos y pentágonos. Fueron descritos por primera vez en 1937 por Michael Goldberg (1902-1990).[1] Están definidos por tres propiedades: cada cara es un pentágono o un hexágono, exactamente tres caras se encuentran en cada vértice y tienen simetría icosaédrica. No poseen necesariamente simetría especular; y por ejemplo $GP(5,3)$ y $GP(3,5)$ son quirales uno respecto al otro. Un poliedro de Goldberg es un poliedro conjugado de una esfera geodésica.

Poliedros icosaédricos de Goldberg con pentágonos en rojo
$GP(1,4)= {5+,3} 1,4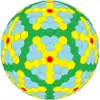$	$GP(4,4)= {5+,3} 4,4$
$GP(7,0)= {5+,3} 7,0$	$GP(3,5)= {5+,3} 3,5$
$GP(10,0)= {5+,3} 10,0$ Equilátero y esférico

Una consecuencia de la característica de Euler es que un poliedro de Goldberg siempre tiene exactamente doce caras pentagonales. La simetría icosaédrica asegura que los pentágonos sean siempre regulares y que siempre haya 12 de ellos. Si los vértices no están restringidos a una esfera, el poliedro se puede construir con caras planas equiláteras (pero no en general equiangulares).

Ejemplos simples de poliedros de Goldberg incluyen el dodecaedro y el icosaedro truncado. Se pueden describir otras formas realizando el movimiento del caballo de ajedrez de un pentágono al siguiente: primero se deben dar $m$ en una dirección; luego se debe girar 60° a la izquierda; y finalmente de deben dar $n$ pasos. Tal poliedro se denota $GP(m, n).$ Un dodecaedro es $GP(1,0)$ y un icosaedro truncado es $GP(1,1).$

Se puede aplicar una técnica similar para construir poliedros con simetría tetraédrica y simetría octaédrica. Estos poliedros tendrán triángulos o cuadrados en lugar de pentágonos. Estas variaciones tienen subíndices de números romanos que indican el número de lados en las caras que no son hexagonales: $GP III (n, m),$ $GP IV (n, m),$ y $GP V (n, m).$

Elementos

El número de vértices, aristas y caras de GP(m,n) se puede calcular a partir de m y n, con T = m² + mn + n² = (m + n)² − mn, dependiendo de uno de los tres sistemas de simetría.[2] El número de caras no hexagonales se puede determinar utilizando la característica de Euler, como se demuestra en el artículo correspondiente.

Simetría	Icosaédrica	Octaédrica	Tetraédrica
Base	Dodecaedro GP_V(1,0)= {5+,3}_1,0	Cubo GP_IV(1,0)= {4+,3}_1,0	Tetraedro GP_III(1,0)= {3+,3}_1,0
Imagen
Símbolo	GP_V(m,n)= {5+,3}_m,n	GP_IV(m,n)= {4+,3}_m,n	GP_III(m,n)= {3+,3}_m,n
Vértices	$20T$	$8T$	$4T$
Aristas	$30T$	$12T$	$6T$
Caras	$10T+2$	$4T+2$	$2T+2$
Caras por tipo	12 {5} y 10(T − 1) {6}	6 {4} y 4(T − 1) {6}	4 {3} y 2(T − 1) {6}

Construcción

La mayoría de los poliedros de Goldberg se pueden construir utilizando la notación de poliedros de Conway a partir de semillas de (T)etraedro, (C)ubo y (D)odecaedro. El operador achaflanado, c, reemplaza todas las aristas por hexágonos, transformando GP(m,n) a GP(2m,2 n), con un multiplicador T de 4. El operador kis truncado, y = tk, genera GP(3,0), transformando GP(m, n) a GP(3m,3n), con un multiplicador T de 9.

Para formas de clase II, el operador dual kis, z = dk, transforma GP(a,0) en GP(a,a), con un multiplicador T de 3. Para formas de clase III, el operador girado, w, genera GP(2,1), con un multiplicador T de 7. Un generador de girado en sentido horario y antihorario, ww = wrw genera GP(7,0 ) en la clase I. En general, un girado puede transformar un GP(a,b) en GP(a + 3b,2ab) para a > b y la misma dirección quiral. Si se invierten las direcciones quirales, GP(a,b) se convierte en GP(2a + 3b,a − 2b) si a ≥ 2b, y GP(3a + b,2b − a) si a < 2b.

Ejemplos

Poliedros de clase I
Frecuencia	(1,0)	(2,0)	(3,0)	(4,0)	(5,0)	(6,0)	(7,0)	(8,0)	(m,0)
T	1	4	9	16	25	36	49	64	m²
Icosaédrico (Goldberg)	Dodecaedro regular	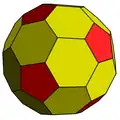Dodecaedro achaflanado		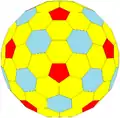				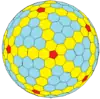	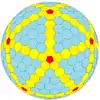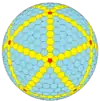más
Octaédrico	Cubo	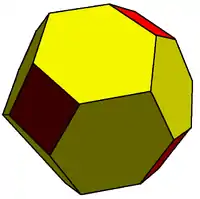Cubo achaflanado		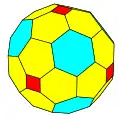		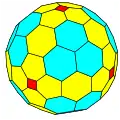			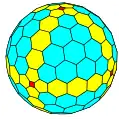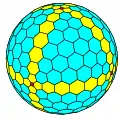más
Tetraédrico	Tetraedro	Tetraedro achaflanado				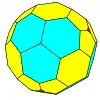		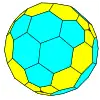	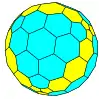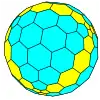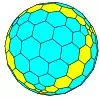más

Poliedros de clase II
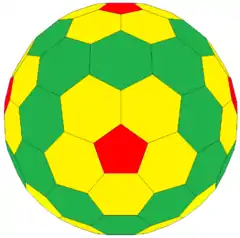
Frecuencia	(1,1)	(2,2)	(3,3)	(4,4)	(5,5)	(6,6)	(7,7)	(8,8)	(m,m)
T	3	12	27	48	75	108	147	192	3m²
Icosaédrico (Goldberg)	Icosaedro truncado									más
Octaédrico	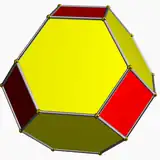Octaedro truncado				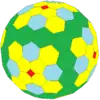				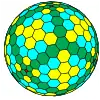	más
Tetraédrico	Tetraedro truncado		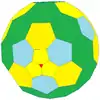						más

Poliedros de clase III
Frecuencia	(1,2)	(1,3)	(2,3)	(1,4)	(2,4)	(3,4)	(5,1)	(m,n)
T	7	13	19	21	28	37	31	m²+mn+n²
Icosaédrico (Goldberg)								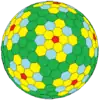más
Octaédrico		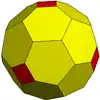						más
Tetraédrico								más

Véase también

Cápside
Esfera geodésica
Fullereno
Notación de poliedros de Conway
Construcción de Goldberg-Coxeter

Referencias

Greg N. Frederickson (1997). Dissections: Plane and Fancy. Cambridge University Press. pp. 141 de 310. ISBN 9780521525824. Consultado el 27 de octubre de 2022.
Clinton’s Equal Central Angle Conjecture, JOSEPH D. CLINTON

Bibliografía

Goldberg, Michael (1937). «A class of multi-symmetric polyhedra». Tohoku Mathematical Journal 43: 104-108.
Joseph D. Clinton, Clinton’s Equal Central Angle Conjecture
Hart, George (2012). «Goldberg Polyhedra». En Senechal, Marjorie, ed. Shaping Space (2nd edición). Springer. pp. 125-138. ISBN 978-0-387-92713-8. doi:10.1007/978-0-387-92714-5_9.
Hart, George (18 de junio de 2013). «Mathematical Impressions: Goldberg Polyhedra». Simons Science News.
Schein, S.; Gayed, J. M. (25 de febrero de 2014). «Fourth class of convex equilateral polyhedron with polyhedral symmetry related to fullerenes and viruses». Proceedings of the National Academy of Sciences (en inglés) 111 (8): 2920-2925. Bibcode:2014PNAS..111.2920S. ISSN 0027-8424. PMC 3939887. PMID 24516137. doi:10.1073/pnas.1310939111.

Enlaces externos

Icosaedro geodésico dual
Variaciones de Goldberg: Nuevas formas para jaulas moleculares Los hexágonos planos y los pentágonos se unen en un nuevo giro sobre el viejo poliedro, por Dana Mackenzie , 14 de febrero de 2014

Datos: Q15735747
Multimedia: Goldberg polyhedra / Q15735747

Este artículo ha sido escrito por Wikipedia. El texto está disponible bajo la licencia Creative Commons - Atribución - CompartirIgual. Pueden aplicarse cláusulas adicionales a los archivos multimedia.

[GNF-1] Greg N. Frederickson (1997). Dissections: Plane and Fancy. Cambridge University Press. pp. 141 de 310. ISBN 9780521525824. Consultado el 27 de octubre de 2022.

[2] Clinton’s Equal Central Angle Conjecture, JOSEPH D. CLINTON