Dodecaedro biselado
En geometría, el dodecaedro biselado (también denominado dodecaedro achaflanado o triacontaedro rómbico truncado) es un politopo convexo con 80 vértices, 120 aristas y 42 caras: 30 hexágonos y 12 pentágonos. Está construido como el achaflanado (truncamiento de aristas) de un dodecaedro regular. Los pentágonos se reducen de tamaño y se añaden nuevas caras hexagonales en lugar de todas las aristas originales. Su dual es el pentaquis icosidodecaedro.
| Dodecaedro biselado | ||
|---|---|---|
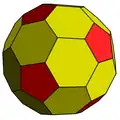 Imagen del sólido | ||
| Tipo |
Poliedro de Goldberg (GV(2,0)= {5+,3}2,0) Fullereno (C80)[1] Sólido casi coincidente de Johnson | |
| Caras |
12 pentágonos 30 hexágonos irregulares | |
| Aristas | 120 (2 tipos) | |
| Vértices | 80 (2 tipos) | |
| Configuración de vértices |
60 (5.6.6) 20 (6.6.6) | |
| Grupo de simetría | Icosaédrica (Ih) | |
| Poliedro dual | Pentaquis icosidodecaedro | |
| Conway | cD= t5daD= dk5aD | |
| Propiedades | ||
| Politopo convexo, con caras equiláteras | ||
| Desarrollo | ||
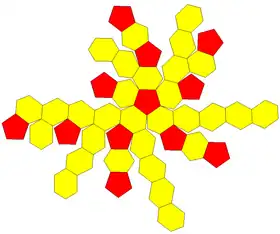 | ||
También se le llama triacontaedro rómbico truncado, construido como el truncado del triacontaedro rómbico. Se le puede llamar con mayor precisión un triacontaedro rómbico truncado de orden 5 porque solo los vértices de orden 5 están truncados.
Estructura
Estos 12 vértices de orden 5 se pueden truncar de modo que todas las raistas tengan la misma longitud. Las 30 caras rómbicas originales se convierten en hexágonos no regulares y los vértices truncados se convierten en pentágonos regulares.
Las caras del hexágono pueden ser equiláteras pero no regulares, con simetría D2. Los ángulos en los dos vértices con configuración de vértices 6.6.6 miden y en los cuatro vértices restantes con disposición 5.6.6, miden 121.717° cada uno.
Es el poliedro de Goldberg GV(2,0), que contiene caras pentagonales y hexagonales.
También representa la envolvente exterior de la proyección ortogonal centrada en una celda del 120-celdas, uno de los seis 4-politopos regulares convexos.
Química
Esta es la forma del fullereno C80; por lo que a veces esta forma se denomina C80(Ih) para describir su simetría icosaédrica y distinguirla de otros fullerenos de 80 vértices pero menos simétricos. Es uno de los cuatro fullerenos encontrados por Deza, Deza y Grishukhin (1998) que tienen un esqueleto que puede ser incrustable isométricamente en un espacio L1.

Poliedros relacionados
Este poliedro se parece mucho al icosaedro truncado uniforme, que cuenta con 12 pentágonos pero tan solo con 20 hexágonos.
 Triacontaedro rómbico truncado
Triacontaedro rómbico truncado
G(2,0) Icosaedro truncado
Icosaedro truncado
G(1,1) Proyección ortogonal centrada en celda del 120-celdas
Proyección ortogonal centrada en celda del 120-celdas
A partir del dodecaedro biselado se pueden generar más poliedros mediante las operaciones descritas según la notación de poliedros de Conway básica. El dodecaedro achaflanado en cremallera forma un icosaedro truncado achaflanado, que también corresponde al poliedro de Goldberg (2,2).
| semilla | ambo | truncado | cremallera | expandido | bisel | romo | chaflán | remolino |
|---|---|---|---|---|---|---|---|---|
 cD= G(2,0) cD |
 acD acD |
 tcD tcD |
 zcD= G(2,2) zcD |
 ecD ecD |
 bcD bcD |
 scD scD |
 ccD= G(4,0) ccD |
 wcD= G(4,2) wcD |
| dual | unión | aguja | n-plicado | orto | medial | giro | chaflán dual | remolino dual |
 dcD dcD |
 jcD jcD |
 ncD ncD |
 kcD kcD |
 ocD ocD |
 mcD mcD |
 gcD gcD |
 dccD dccD |
 dwcD dwcD |
Icosaedro truncado biselado
| Icosaedro truncado biselado | |
|---|---|
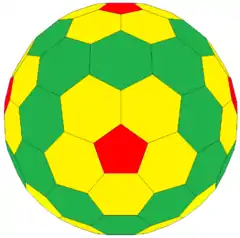 | |
| Poliedro de Goldberg | GV(2,2)= {5+,3}2,2 |
| Notación de Conway | ctI |
| Fullereno | C240 |
| Caras | 12 pentágonos 110 hexágonos (3 tipos) |
| Aristas | 360 |
| Vértices | 240 |
| Simetría | Ih, [5,3], (*532) |
| Dual | Hexapentaquis dodecaedro biselado |
| Propiedades | Convexo |
En geometría, el icosaedro truncado biselado es un poliedro convexo que cuenta con 240 vértices, 360 aristas y 122 caras, (110 hexágonos y 12 pentágonos).
Se construye mediante una operación de achaflanado sobre un icosaedro truncado, agregando nuevos hexágonos en lugar de las aristas originales. También se puede construir como una operación cremallera zip (= dk = dual del n-plicado de) a partir del dodecaedro biselado. En otras palabras, elevar pirámides pentagonales y hexagonales sobre un dodecaedro achaflanado (operación n-plicado o kis) producirá un poliedro geodésico (2,2). Tomando el dual de este último se obtiene el poliedro de Goldberg (2,2), que es el icosaedro truncado achaflanado, y también es el fullereno C240.
Dual
Su dual, el hexapentaquis dodecaedro biselado, tiene 240 caras triangulares (agrupadas en 60 (azules), 60 (rojas) alrededor de 12 vértices de simetría quíntuple y 120 alrededor de 20 vértices de simetría séxtuple), 360 aristas, y 122 vértices.

Hexapentaquis dodecaedro biselado
Referencias
- «C80 Isomers». Archivado desde el original el 12 de agosto de 2014. Consultado el 5 de agosto de 2014.
Bibliografía
- Deza, Antoine; Deza, Michel; Grishukhin, Viatcheslav (October 1998). «Fullerenes and coordination polyhedra versus half-cube embeddings». Discrete Mathematics 192 (1–3): 41-80. doi:10.1016/S0012-365X(98)00065-X.
- Goldberg, Michael (1937). «A class of multi-symmetric polyhedra». Tohoku Mathematical Journal 43: 104-108.
- Hart, George (2012). «Goldberg Polyhedra». En Senechal, Marjorie, ed. Shaping Space (2nd edición). Springer. pp. 125–138. ISBN 978-0-387-92713-8. doi:10.1007/978-0-387-92714-5_9.
- Hart, George (18 de junio de 2013). «Mathematical Impressions: Goldberg Polyhedra». Simons Science News.