Potencia perfecta
En matemáticas, una potencia perfecta es un número natural que es producto de factores naturales iguales, o dicho de otro modo, un número entero que se puede expresar como un cuadrado o como una potencia entera mayor que uno. Más formalmente, n es una potencia perfecta si existen dos números naturales m > 1, y k > 1 tales que mk = n. En este caso, n puede llamarse k-ésima potencia perfecta. Si k = 2 o k = 3, entonces n se llama cuadrado perfecto o cubo, respectivamente. A veces, 0 y 1 también se consideran potencias perfectas (0k = 0 para cualquier k > 0, 1k = 1 para cualquier k).
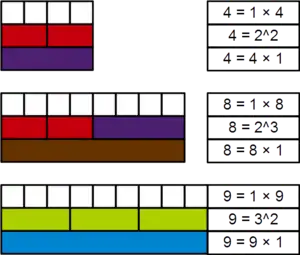
Ejemplos y sumas
Se puede generar una sucesión de potencias perfectas iterando a través de los valores posibles para m y k. Las primeras potencias perfectas ascendentes en orden numérico (mostrando potencias duplicadas) son (sucesión A072103 en OEIS):
La suma de los recíprocos de las potencias perfectas (incluyendo duplicados como 34 y 92, ambos iguales a 81) es 1:
lo que se puede demostrar de la siguiente manera:
Las primeras potencias perfectas sin duplicados son:
- (a veces 0 y 1), 4, 8, 9, 16, 25, 27, 32, 36, 49, 64, 81, 100, 121, 125, 128, 144, 169, 196, 216, 225, 243, 256, 289, 324, 343, 361, 400, 441, 484, 512, 529, 576, 625, 676, 729, 784, 841, 900, 961, 1000, 1024, ... (sucesión A001597 en OEIS)
La suma de los recíprocos de las potencias perfectas p sin duplicados es:[1]
donde μ(k) es la función de Möbius y ζ(k) es la función zeta de Riemann.
Según Euler, Goldbach mostró (en una carta ahora perdida) que la suma de 1p − 1 sobre el conjunto de potencias perfectas p, excluyendo 1 y excluyendo duplicados, es 1:
Esto a veces se conoce como el teorema de Goldbach-Euler.
Detección de potencias perfectas
Detectar si un número natural n dado es o no una potencia perfecta se puede lograr de muchas maneras diferentes, con niveles variables de complejidad. Uno de los métodos más simples es considerar todos los valores posibles para k en cada uno de los divisores de n, hasta . Entonces, si los divisores de son , entonces uno de los valores debe ser igual a n si n es una potencia perfecta.
Este método se puede simplificar de inmediato considerando en su lugar solo los valores primos de k. Esto se debe a que si para un número compuesto donde p es primo, entonces esto se puede reescribir simplemente como . Debido a este resultado, el valor mínimo de k debe ser necesariamente primo.
Si se conoce la factorización completa de n, descrita como donde los son primos distintos, entonces n es una potencia perfecta si y solo si , donde mcd denota el máximo común divisor. Como ejemplo, considérese n= 296·360·724. Como el mcd(96, 60, 24)= 12, n es una potencia perfecta de 12 (y una potencia perfecta de 6, 4, cúbica y cuadrada, ya que 6, 4, 3 y 2 dividen a 12).
Brechas entre potencias perfectas
En 2002, el matemático rumano Preda Mihăilescu demostró que el único par de potencias perfectas consecutivas es 23= 8 y 32= 9, demostrando así la conjetura de Catalan.
La conjetura de Pillai establece que para cualquier número entero positivo k dado, solo hay un número finito de pares de potencias perfectas cuya diferencia es k. Este es un problema sin resolver.[2]
Véase también
Referencias
- Weisstein, Eric W. «Perfect Power». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Weisstein, Eric W. «Pillai's Conjecture». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Daniel J. Bernstein (1998). «Detecting perfect powers in essentially linear time». Mathematics of Computation 67 (223): 1253-1283. doi:10.1090/S0025-5718-98-00952-1.