Análisis de frecuencia acumulada
La frecuencia acumulada o frecuencia acumulativa es la frecuencia de ocurrencia de valores de un fenómeno menor que un valor de referencia. El fenómeno puede ser una variable aleatoria que varia en el tiempo o en el espacio. La frecuencia acumulada se llama también frecuencia de no−excedencia. El análisis de la frecuencia acumulada se hace con el propósito de obtener una idea de cuantas veces ocurriría un cierto fenómeno lo que puede ser instrumental en describir o explicar una situación en la cual el fenómeno juega un papel importante, o en planificar intervenciones, por ejemplo en el control de inundaciones.[1]
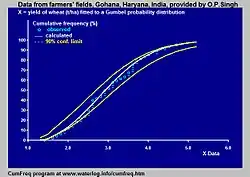
Principios
Definición
El análisis de la frecuencia acumulada se aplica a una colección de datos observados de un fenómeno (X).[2] La colección puede ser en dependencia del tiempo (por ejemplo la lluvia medida en un sitio) o del espacio (por ejemplo cosechas de cultivos en el área), o puede tener otra dependencia.
La frecuencia acumulada es la frecuencia estadística F(X≤Xr) con que el valor de un variable aleatoria (X) es menor que o igual a un valor de referencia (Xr).
La frecuencia acumulada relativa se deja escribir como Fc(X≤Xr), o en breve Fc(Xr), y se calcula de:
- Fc (Xr) = MXr / N
donde MXr es el número de datos X con un valor menor que o igual a Xr, y N es número total de los datos.
En breve se escribe:
- Fc = M / N
Cuando Xr=Xmin, donde Xmin es el valor mínimo observado, se ve que Fc=1/N, porque M=1. Por otro lado, cuando Xr=Xmax, donde Xmax es el valor máximo observado, se ve que Fc=1, porque M=N.
En porcentaje la ecuación es:
- Fc(%) = 100 M / N
Probabilidad
La probabilidad cumulativa ℙ(X≤Xr) − es decir la probabilidad que X será menor que o igual a Xr − se puede estimar a base de la frecuencia acumulada relativa Fc como:
- Pc (Xr) = MXr / (N+1)
En breve se puede notar:
- Pc = M/(N+1)
Aquí se ha introducido el denominador N+1 en vez de N para crear la posibilidad que X puede ser mayor que Xmax ya que ahora Pc(Xmax) es menor de 1. Existen otras propuestas para el denominador N+1, pero éstas a la vez son consideradas incorrectas.[3]
Ordenación por magnitud
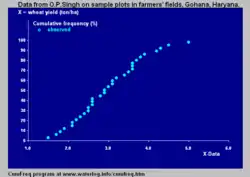
Una manerea alternativa para calcular Pc es mediante ordenación de los datos por magnitud. Cuando los datos X están ordenados por magnitud en una serie ascendente, primero el mínimo y al fin el máximo, y Ri es el número del rango de un cierto Xi en la serie, la probabilidad acumulada se escribe como:
- Pc(Xi) = Ri / (N+1)
o en breve:
- Pc = Ri / (N+1)
Por otro lado, cuando los datos están ordenados en una secuencia descendente, primero el máximo y finalmente el mínimo, y Rj es el número de rango de un cierto Xj, la expresión de la probabilidad acumulada es:
- Pc(Xj) = 1 − Rj / (N+1)
o en breve:
- Pc = 1 − Rj / (N+1)
Adaptación a distribuciones de probabilidad
Distribución continua
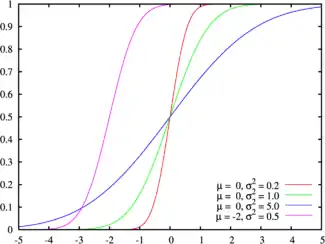
A fin de formular la distribución de frecuencia acumulativa como una ecuación matemática evitando la presentación de una tabla, se adapta esta distribución a una distribución de probabilidad acumulativa.[2]
La ecuación también ayuda en la interpolación y la extrapolación.
Sin embargo, la extrapolación de una distribución de frecuencia puede ser un fuente de errores. Un posible error es que la distribución de frecuencia no sigue la distribución de probabilidad afuera del rango observado.
Cualquier ecuación que da el valor 1 cuando integrado de un límite inferior a un límite superior que corresponden con los datos, puede servir como distribución de probabilidad.
Existen dos procedimientos para la acomodación de distribuciones de probabilidad:[2]
- el método paramétrico, determinando los parámetros como medio y desviación estándar de los datos X
- el método de regresión, linearizando la distribución de probabilidad por una transformación y determinando los parámetros con una regresión lineal de Pc transformado (aquí Pc se obtiene del método de ordenación por magnitud) sobre los datos X transformados
Aplicación de ambos métodos empleando por ejemplo la:
- distribución normal
- distribución log-normal
- distribución exponencial
- distribución de Gumbel
- distribución de Pareto
- distribución de Weibull
a menudo no produce resultados que difieren significativamente. Además, diferentes distribuciones de probabilidad pueden arrojar resultados similares con diferencias relativamente pequeñas en comparación con el ancho del intervalo de confianza. Entonces no siempre es fácil decidir cual distribución rinde los mejores resultados.
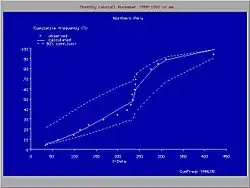
Distribución discontinua
Es posible de introducir una discontinuidad, separando el rango de datos en dos partes con distribuciones diferentes. La introducción de la continuidad es útil cuando la cola de la distribución, y los valores extremos, desvían de la distribución de la masa mediana de los datos.
La introducción también ha sido instrumental para el análisis de las lluvias en el norte de Perú donde el clima depende del comportamiento del corriente El Niño en el océano Pacífico. Cuando El Niño se extiende más allá del sur de Ecuador llegando a la costa Peruana, el clima en el norte de Perú se vuelve trópico húmedo. Cuando El Niño no llega al Perú, el clima es semi−árido. Por esta razón, las lluvias extremas exhiben una distribución de frecuencia diferente de las lluvias moderadas.[4]
Pronóstico
Incertitud
Se puede cuestionar si la distribución de frecuencias acumuladas es utilizable para predicciones. Por ejemplo, es que se puede predecir cuantas veces una cierta descarga de un río será sobrepasado en los años 2000 a 2050, dado un serie de descargas medidas durante los años 1950 a 2000. La respuesta es: sí, a condición que las circunstancias ambientales del río se cambiarán. Cuando las condiciones ambientales se alteran (por ejemplo por medidas de ingeniería civil, Ingeniería hidráulica, o por modificación del comportamiento de la lluvia debido a un cambio climático, el pronóstico será sujeto de un error sistemático. Aún, cuando no haya alteraciones sistemáticas, el pronóstico puede ser sujeto a un error al azar, porque las descargas obeservadas durante 1950 a 2000 por casualidad podrían haber sido mayores o menores que normal, y al contrario las descargas de 2000 a 2050 por casualidad podrán ser menores o mayores de lo normal.
Intervalos de confianza
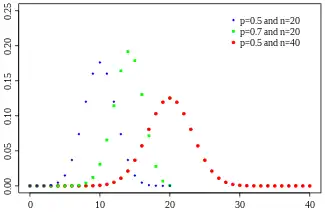
Para determinar la confianza de predicciones a base de una distribución de frecuencias acumuladas observadas la teoría de la probabilidad puede ayudar en la construcción de intervalos de confianza que indican el rango probable del error al azar. En el caso de frecuencia acumulada hay solo dos posibilidades: un valor de referencia X es excedido o no. La suma de los dos siempre es 1 o 100%. Por ello la distribución binomial se deja utilizar para estimar el intervalo de confianza.
De acuerdo a la teoría de la distribución binomial, la desviación estándar Sd se puede calcular de:
- Sd =√{Pc(1−Pc)/N}
donde Pc es la probabilidad cumulativa, y N es el número de datos. Se ve que la desviación estándar disminuye cuando más grande el número de observaciones N.
La determinación del intervalo de confianza de Pc emplea la prueba t de Student utilizando la distribución t de Student. El valor de t depende del número de datos y el nivel de confianza del intervalo de confianza. El límite inferior (Li) y el límite superior (Ls) del intervalo de confianza de Pc bajo la condición que este tenga una distribución simétrica se calculan como:
- Li = Pc − t . Sd
- Ls = Pc + t . Sd
No obstante, aunque la distribución binomial es simétrica alrededor del medio (cuando Pc es 0.5), ella se vuelve más y más ladeado cuando Pc se aproxima a 0 o 1. Por ello se puede usar Pc y 1−Pc como factores de ponderación en la asignación de t.Sd a Li y Ls :
- Li = Pc − 2 Pc . t . Sd
- Ls = Pc + 2 (1−Pc) . t . Sd
y se ve que cuando Pc es 0.5 estas expresiones son equivalentes a las dos previas.
| Ejemplo N = 25, Pc = 0.8, Sd = 0.08, nivel de confianza es 90%, t = 1.71, Li = 0.70, Ls = 0.85 Entonces se concluye con 90% de confianza que 0.70 < Pc < 0.85 Todavía existe 10% de probabilidad que Pc < 0.70, o Pc > 0.85 |
Período de retorno
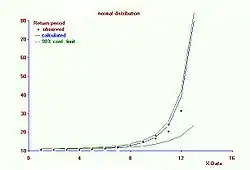
La frecuencia acumulada Pc se puede llamar también probabilidad de no−excedencia. La probabilidad de excedencia (Pe) se define como:
- Pe = 1 − Pc
El período de retorno (período de recurrencia, período de repetición) se defina como:
- T = 1/Pe
indicando el número esperado de observaciones se tiene que hacer antes de encontrar de nuevo un valor del variable estudiado mayor que el valor usado en la determinación de T.
El límite superior (Ts) y el límite inferior (Ti) de confianza del período de retorno T son respectivamente:
- Ts= 1/(1−Ls)
- Ti= 1/(1−Li)
Para valores extremos del variable estudiado, Ls se aproxima a 1 y un cambio pequeño de Ls da lugar a un cambio grande de Ts. Por ello, el período de retorno estimado para eventos extremos está sujeto a un error al azar grande. Además, los intervalos de confianza calculados son válidos a largo plazo. Para pronósticos a corto plazo los intervalos pueden ser más amplios. Junto con la suguridad limitada (menos de 100%) usada en la prueba−t, esto explica por ejemplo porque una lluvia con período de recurrencia de 100 años podría manifestarse 2 veces en 10 años.
La noción estricta de período de retorno solo tiene significado cuando se trata de un fenómeno que depende del tiempo. En este caso el período de retorno corresponde al tiempo de espera hasta que el evento de excedencia ocurre de nuevo. La unidad de tiempo iguala a la unidad de tiempo de las mediciones del fenómeno. Por ejemplo, para lluvias diarias el período se mide en días, y para lluvias anuales en años.
Histograma
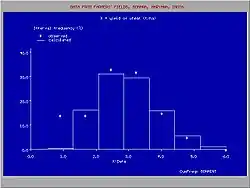
Los datos observados se dejan ordenar en clases o grupos con número serial k. Cada grupo tiene un límite inferior (Ik) y un límite superior (Sk). Cuando un grupo (k) contiene mk datos y el número total de datos es N, la frecuencia estadística relativa del grupo (Fg) se determina como:
- Fg (Ik<X≤Sk) = mk / N
En breve:
- Fg = m/N
o en porcentaje:
- Fg(%) = 100m/N
La presentación de todas las clases en un gráfico da una distribución de frecuencias o histograma. Histogramas que originan de la misma colección de datos y que tienen otros límites de clases son diferentes.
Las histogramas se pueden derivar también de la distribución adaptada de probabilidad:
- Pg = Pc (Sk) − Pc (Ik)
Puede haber una diferencia entre Fg y Pg a causa de las desviaciones de los datos observados de la distribución adaptada (véase la figura).
Listado de software
Se puede usar un programa de computadora para la construcción de la distribución de frecuencia y probabilidad acumulada, por ejemplo:
Referencias
- Benson, M.A. 1960. Caracteristics of frequency curves based on a theoretical 1000 year record. In: T.Dalrymple (ed.), Flood frequency analysis. U.S. Geological Survey Water Supply paper 1543−A, pp. 51−71
- Frequency and Regression Analysis. Chapter 6 in: H.P.Ritzema (ed., 1994), Drainage Principles and Applications, Publ. 16, pp. 175−224, International Institute for Land Reclamation and Improvement (ILRI), Wageningen, The Netherlands. ISBN 90 70754 3 39 . Bajar de la página : , bajo no. 12, o directamente como PDF :
- Makkonen, L. 2008. Communications in Statistics − Theory and Methods, 37: 460−467
- Cumfreq, a program for cumulative frequency analysis + confidence belt + discontinuity option + return period , bajada libre de :
- Easy fit Archivado el 23 de febrero de 2018 en Wayback Machine., Data analysis & simulation
- MathWorks Benelux (enlace roto disponible en Internet Archive; véase el historial, la primera versión y la última).
- ModelRisk, risk modelling software
- Fitting distrubutions with R , Vito Ricci, 2005
- Automatically fit distributions and parameters to samples
- «StatSoft distribution fitting». Archivado desde el original el 30 de agosto de 2012. Consultado el 28 de junio de 2010.
- Ejemplos de aplicación de CumFreq se encuentran en: Drainage Research in Farmers' Fields: Analysis of Data. Part of project “Liquid Gold” of the International Institute for Land Reclamation and Improvement (ILRI), Wageningen, The Netherlands. On line :