Programación en enteros
Un problema de programación en enteros es un programa de optimización o factibilidad matemática en el cual algunas o todas las variables tienen que ser enteras. En muchos escenarios el término se refiere a programación lineal en enteros (PLE), en el cual la función objetivo y las restricciones (aparte de las restricciones enteras) son lineales.
La programación en enteros es NP-duro. Un caso especial, la programación lineal en enteros 0-1, en el cual las incógnitas son binarias, es uno de los 21 problemas NP-completo de Karp.
Forma estándar y canónica para los PLEs
Un programa lineal en enteros en forma canónica se expresa como:[1]
- ,
y un PLE en forma estándar se expresa como
donde son vectores y es una matriz de valores enteros. Note que similar a los programas lineales, los PLEs que no están en forma estándar pueden ser convertidos a forma estándar eliminando las desigualdades e introduciendo variables artificiales () y reemplazando las variables que no están restringidas en signo con la diferencia de dos variables restringidas en signo
Ejemplo
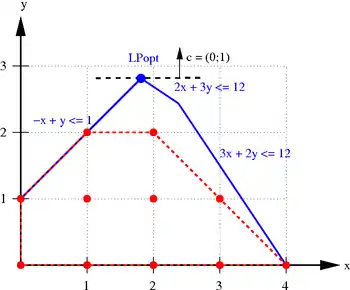
La imagen a la derecha muestra el siguiente problema.
Los puntos enteros factibles se muestran en rojo, y las líneas rojas discontinuas delimitan la región convexa, la cual es el poliedro más pequeño que contiene todos esos puntos. Las líneas de azul, junto con el eje de coordenadas definen el poliedro de la relajación del PL, el cual está dado por las desigualdades sin la restricción de entera. La meta de la optimización es mover la línea de puntos negros tan arriba como se pueda mientras que ésta siga tocando el poliedro. Las soluciones óptimas del problema entero son los puntos y los cuales dan un valor de la función objetivo de 2. El óptimo único de la relajación es con un valor de la función objetivo de 2.8. Note que si la solución de la relajación es redondeada al entero más cercano, ésta no es factible para el PLE.
Variantes
La programación lineal en enteros mixta (PLEM) involucra problemas en los cuales algunas de las variables, , están restringidas a ser enteras, mientras que otras variables pueden no ser enteras.
La programación lineal cero-uno involucra problemas en los cuales las variables son restringidas a los valores 0 o 1. Note que cualquier variable entera acotada puede ser expresada como un combinación de variables binarias.[2] Por ejemplo, dada una variable entera, , ésta puede ser expresada usando variables binarias:
Ejemplos de problemas que pueden ser formulados como PLEs
Un gran número de problemas pueden ser formulados como PLEs. Esto incluye:
- Problema del viajante
- Cobertura de vértice y otros problemas de cubrimiento
- Set packing y otros problemas de empacamiento
- Satisfactibilidad booleana
Puesto que la programación lineal en enteros está en NP (las soluciones pueden ser verificadas en tiempo polinomial) y existen problemas NP-completos que pueden ser polinomialmente reducidos a los PLEs, entonces, la programación lineal en enteros es NP-completo.
Aplicaciones
Existen dos razones principales para usar variables enteras cuando se modelan problemas como programas lineales:
- Las variables enteras representan cantidades que solo pueden ser enteras. Por ejemplo, no es posible construir 3.7 vehículos.
- Las variables enteras representan decisiones, por lo que deberían tomar solo los valores 0 o 1.
Estas consideraciones ocurren frecuentemente en la práctica y por consiguiente la programación lineal en enteros puede ser usada en muchas áreas de aplicación, algunas de las cuales son brevemente descritas a continuación.
Plan de producción
La PLEM tiene muchas aplicaciones en la producción industrial, incluyendo modelado trabajo-tienda. El plan de producción en la agricultura implica determinar el rendimiento de la producción para varios cultivos que pueden compartir recursos (e.g., tierra, labor, fondo para fertilizador de semillas, etc.). Un objetivo posible es maximizar la producción total, sin exceder los recursos disponibles. En algunos casos, esto puede ser expresado en términos de un programa lineal, pero las variables deben ser restringidas a los enteros.
Planificación
Estos problemas involucran planificación de vehículos y servicios en redes de transportación. Por ejemplo, un problema puede implicar asignar autobuses o metros a rutas individuales para que un horario sea cumplido, y también equiparlos con chóferes. Aquí las variables de decisión binarias indican dónde un autobús o metro es asignado a una ruta y dónde un chófer es asignado a un tren o metro en particular.
Redes de telecomunicaciones
El objetivo de estos problemas es diseñar una red de líneas para instalar por lo que un conjunto predefinido de requerimientos de comunicación es conocido y el costo total de la red es minimal.[3] Esto requiere optimizar la topología de la red junto con la configuración de capacidades de las diferentes líneas. En muchos casos, las capacidades están restringidas a cantidades enteras. Usualmente existen, dependiendo de la tecnología usada, restricciones adicionales que pueden ser modeladas como desigualdades lineales con variables enteras o binarias.
Redes celulares
La tarea de planificar frecuentemente en redes de teléfonos GSM implica distribuir frecuencias disponibles a través de las antenas para que los usuarios puedan ser servidos y la interferencia sea minimizada entre las antenas.[4] Este problema puede ser formulado como un programa lineal en enteros en el cual las variables binarias indican donde una frecuencia es asignada a una antena.
Algoritmos
La forma sencilla de resolver un PLE es simplemente eliminar la restricción x que es entera, resolver el correspondiente PL (llamado relajación PL del PLE), y entonces redondear la solución del PL relajado. Pero, esta solución no solo puede no ser óptima, sino que incluso puede no ser factible, o sea que puede violar alguna restricción.
Usando unimodularidad total
Mientras que en general la solución del problema relajado no se garantizará que sea óptima, si el PLE tiene la forma tal que donde y son todos enteros y es totalmente unimodular, entonces toda solución factible básica es entera. Consecuentemente, la solución retornada por el algoritmo símplex se garantiza que es entera. Para demostrar que cada solución factible básica es entera, sea una solución factible básica cualquiera. Puesto que es factible, sabemos que . Sea los elementos correspondientes a las columnas básicas para la solución básica . Por definición de una base, existe una submatriz cuadrada de con columnas linealmente independientes tales que .
Puesto que las columnas de son linealmente independientes y es cuadrada, es no singular, y por consiguiente, es unimodular y así . También, debido a que es no singular, es inversible y por consiguiente . Por definición, . Note que denota la conjugada de y es entera porque es entera. Por consiguiente,
De esta forma, si la matriz de un PLE es totalmente unimodular, en vez de usar un algoritmo de PLE, el algoritmo símplex puede ser usado para resolver la relajación de PL y la solución será entera
Algoritmos exactos
Cuando la matriz no es totalmente unimodular, existen una variedad de algoritmos que pueden ser usados para resolver los programas lineales en enteros exactamente. Una clase de estos algoritmos son los métodos de planos cortantes los cuales funcionan resolviendo la relajación de PL y entonces añadir restricciones lineales que lleve la solución a ser entera sin excluir algún punto entero factible.
Otra clase de algoritmos son las variantes de los métodos de ramificación y acotación Por ejemplo, el método ramificación y corte que combina los métodos de ramificación y acotación y planos cortantes. Los algoritmos de ramificación y acotación poseen un gran número de ventajas sobre algoritmos que solo usan planos cortantes. Una ventaja es que los algoritmos pueden ser tempranamente terminados y siempre y cuando al menos una solución entera ha sido encontrada, una factible, aunque no necesariamente óptima, ésta puede ser retornada. Además, las soluciones de los PL relajados pueden ser usadas para proveer un estimado del caso peor de cuán lejos de la optimalidad está la solución retornada. Finalmente, los métodos de ramificación y acotación pueden ser usados para retornar múltiples soluciones óptimas.
Lenstra en 1983 demostró,[5] que cuando el número de variables es fijo, los problemas de programación en enteros pueden ser resueltos en un tiempo polinomial.
Métodos heurísticos
Puesto que la programación lineal en enteros es NP-completo, muchas instancias de problemas son intratables, por lo que métodos heurísticos deben ser usados en su lugar. Por ejemplo, búsqueda tabú puede ser usada para buscar soluciones de PLEs.[6] Para usar búsqueda tabú para resolver PLEs, los movimientos pueden ser definidos como incrementar o decrementar una variable entera de una solución factible, mientras que todas las demás variables enteras se mantienen constantes. Las variables irrestrictas pueden entonces ser resueltas. Memoria de término corto puede consistir de soluciones previamente intentadas mientras que memoria de término medio puede consistir de valores para las variables enteras que han resultado en valores altos de la función objetivo (asumiendo que el PLE es un problema de maximización). Finalmente, memoria de término largo puede guiar la búsqueda hacia los valores enteros que no han sido previamente intentados.
Otros métodos heurísticos que pueden ser usados para resolver PLEs incluye
- Hill climbing
- Simulated annealing
- Optimización de búsqueda reactiva
- Algoritmo de la colonia de hormigas
- Red neuronal Hopfield
Existen también una variedad de otras heurísticas de problemas específicos, tales como heurísitica k-opt para el TSP. Note que una desventaja de los métodos heurísticos es que si fallan en encontrar una solución, no puede ser determinado donde es porque no hay solución factible, o donde el algoritmo simplemente no pudo encontrar una solución. Además, es usualmente imposible cuantificar cuán cerca de la solución óptima está una solución retornada por estos métodos.
Referencias
- Papadimitriou, C.H.; Steiglitz, K. (1998). Combinatorial optimization: algorithms and complexity. Mineola, NY: Dover. ISBN 0486402584.
- Williams, H.P. (2009). Logic and integer programming. International Series in Operations Research & Management Science 130. ISBN 978-0-387-92280-5.
- Borndörer, R.; M. (2012). «Designing telecommunication networks by integer programming».
- Sharma, Deepak (2010). «Frequency Planning».
- H.W.Lenstra, "Integer programming with a fixed number of variables", Mathematics of operations research, Vol 8, No 8, November 1983
- Glover, F. (1989). «Tabu search-Part II». ORSA Journal on computing 1 (3): 4-32. doi:10.1287/ijoc.2.1.4.
Lectura complementaria
- George L. Nemhauser; Laurence A. Wolsey (1988). Integer and combinatorial optimization. Wiley. ISBN 978-0-471-82819-8.
- Alexander Schrijver (1998). Theory of linear and integer programming. John Wiley and Sons. ISBN 978-0-471-98232-6.
- Laurence A. Wolsey (1998). Integer programming. Wiley. ISBN 978-0-471-28366-9.
- Dimitris Bertsimas; Robert Weismantel (2005). Optimization over integers. Dynamic Ideas. ISBN 978-0-9759146-2-5.
- John K. Karlof (2006). Integer programming: theory and practice. CRC Press. ISBN 978-0-8493-1914-3.
- H. Paul Williams (2009). Logic and Integer Programming. Springer. ISBN 978-0-387-92279-9.
- Michael Jünger, Thomas M. Liebling, Denis Naddef, George Nemhauser, William R. Pulleyblank, Gerhard Reinelt, Giovanni Rinaldi and Laurence A. Wolsey, ed. (2009). 50 Years of Integer Programming 1958-2008: From the Early Years to the State-of-the-Art. Springer. ISBN 978-3-540-68274-5.
- Der-San Chen; Robert G. Batson; Yu Dang (2010). Applied Integer Programming: Modeling and Solution. John Wiley and Sons. ISBN 978-0-470-37306-4.