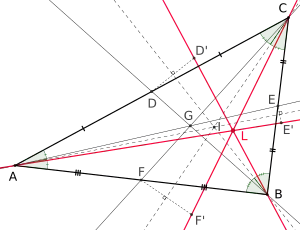
Punto de Lemoine
El punto simediano, punto de Lemoine o punto de Grebe es la intersección de las tres simedianas (líneas simétricas a las medianas con respecto a sus bisectrices asociadas) de un triángulo.
Historia
El matemático francés Émile Lemoine probó la existencia del punto simediano en 1873, y Ernst Wilhelm Grebe publicó un artículo sobre él en 1847. Simon Antoine Jean L'Huillier también observó este punto en 1809.[1]
Ross Honsberger denominó su existencia como "una de las joyas de la corona de la geometría moderna".
Propiedades
En la Enciclopedia de Centros del Triángulo, el punto simediano aparece como el sexto punto, X(6).[2] Descansa en el círculo ortocentroidal, y podría ser cualquier punto de su interior.[3]
El punto simediano de un triángulo con longitudes de lado a, b y c tiene coordenadas trilineales homogéneas [a : b : c].
El punto de Gergonne de un triángulo coincide con el punto simediano de su triángulo de los contactos con la circunferencia inscrita.[4]
El punto simediano de un triángulo ABC puede ser construido de la manera siguiente: sean las líneas tangentes de la circunferencia circunscrita de ABC a través de B y C que se cortan en A', y análogamente, se definen B' y C'; entonces A'B'C' es el triángulo tangencial de ABC, y las líneas AA', BB' y CC' se cruzan en el punto simediano de ABC.[5] Se puede demostrar que estas tres líneas se cortan en un punto utilizando el teorema de Brianchon. La línea AA' es una simediana, lo que puede verse al dibujar el círculo con centro en A' que pasa a través de B y C.
Para la extensión a un tetraedro irregular véase simediana.
Referencias
- Honsberger, Ross (1995), «Chapter 7: The Symmedian Point», Episodes in Nineteenth and Twentieth Century Euclidean Geometry, Washington, D.C.: Mathematical Association of America..
- Encyclopedia of Triangle Centers, accessed 2014-11-06.
- Bradley, Christopher J.; Smith, Geoff C. (2006), «The locations of triangle centers», Forum Geometricorum 6: 57-70..
- Beban-Brkić, J.; Volenec, V.; Kolar-Begović, Z.; Kolar-Šuper, R. (2013), «On Gergonne point of the triangle in isotropic plane», Rad Hrvatske Akademije Znanosti i Umjetnosti 17: 95-106..
- Si ABC es un triángulo rectángulo con el ángulo rectángulo en A, entonces la referencia a AA' debe corregirse, puesto que el punto A' no existe.
Enlaces externos
- Weisstein, Eric W. "Symmedian Punto". Weisstein, Eric W. «Symmedian Point». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.