Recta de Schoch

En geometría, la recta de Schoch es una línea definida a partir de un arbelos, en la que se localizan los centros de una serie de circunferencias que son simultáneamente tangentes al círculo mayor del arbelos, y a una serie de arcos tangentes entre sí en la cúspide intermedia del arbelos. Todas estas circunferencias tienen el mismo tamaño que los círculos de Arquímedes. Su nombre procede de una referencia de Peter Woo al trabajo de Thomas Schoch, que había estudiado la recta junto con los círculos de Schoch.

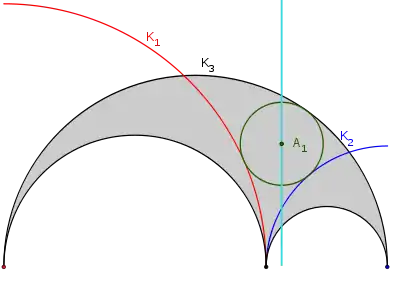
La recta de Schoch (cian) pasa por el punto A₁, y en ella se localizan los centros de los círculos de Arquímedes tangentes al círculo mayor del arbelos y a una serie de arcos tangentes entre sí en la cúspide intermedia del arbelos

Construcción

Un arbelos es una forma delimitada por tres arcos semicirculares mutuamente tangentes con puntos finales colineales, con los dos arcos más pequeños anidados dentro del más grande. Sean los puntos finales de estos tres arcos (en orden en la recta que los contiene) A, B y C. Sean K₁ y K₂ dos arcos más, con centros en A y C, respectivamente, con radios AB y CB. Estos dos arcos son tangentes en B. Ahora, sea K₃ el más grande de los tres arcos del arbelos. A continuación, se traza un círculo tangente a los arcos K₁, K₂ y K₃, cuyo centro es el punto A₁. Este círculo es congruente con los círculos de Arquímedes (es decir, tiene el mismo radio), por lo que es un círculo arquimediano; y es uno de los círculos de Schoch. La recta de Schoch es perpendicular a la línea AC y pasa por el punto A₁. También es la ubicación de los centros de infinitos círculos arqimedianos, los círculos de Woo.[1]

Radio y centro de A₁

Si r=AB/AC y AC = 1, entonces el radio de A₁ es

\rho ={\frac {1}{2}}r\left(1-r\right)

y el centro es

\left({\frac {1}{2}}r\left(-1+3r-2r^{2}\right)~,~r\left(1-r\right){\sqrt {\left(1+r\right)\left(2-r\right)}}\right).

[1]

Referencias

Dodge, Clayton W.; Schoch, Thomas; Woo, Peter Y.; Yiu, Paul (1999), «Those ubiquitous Archimedean circles», Mathematics Magazine 72 (3): 202-213, MR 1706441, doi:10.2307/2690883..

Lecturas adicionales

Okumura, Hiroshi; Watanabe, Masayuki (2004), «The Archimedean circles of Schoch and Woo», Forum Geometricorum 4: 27-34, MR 2057752..

Enlaces externos

van Lamoen, Floor. «Schoch Line." From MathWorld--A Wolfram Web Resource, created by Eric W. Weisstein». Consultado el 11 de abril de 2008.

Datos: Q1878128

Este artículo ha sido escrito por Wikipedia. El texto está disponible bajo la licencia Creative Commons - Atribución - CompartirIgual. Pueden aplicarse cláusulas adicionales a los archivos multimedia.

[dswy-1] Dodge, Clayton W.; Schoch, Thomas; Woo, Peter Y.; Yiu, Paul (1999), «Those ubiquitous Archimedean circles», Mathematics Magazine 72 (3): 202-213, MR 1706441, doi:10.2307/2690883..