Redondez
Se define redondez como una medida de lo que se acerca la forma de un objeto a la de un círculo matemáticamente perfecto. El concepto se aplica en dos dimensiones, haciéndose extensible a las secciones transversales circulares de objetos tridimensionales, como en el caso de semiejes o rodamientos cilíndricos. Cuando se trata de evaluar tolerancias geométricas, el control de un cilindro también puede incluir su fidelidad al eje longitudinal, dando como resultado la cilindricidad. El análogo de la redondez en tres dimensiones (es decir, cuando la forma se compara con una esfera), es la esfericidad.
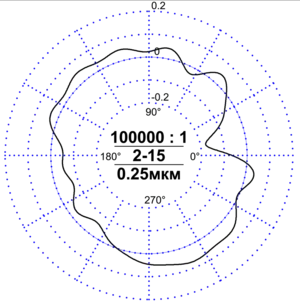
La redondez está dominada por las características generales de la forma más que por la definición de sus bordes y esquinas, o la rugosidad del objeto fabricado. Una elipse suave puede tener una redondez baja, si su excentricidad es elevada. Los polígonos regulares aumentan su redondez a medida que se incrementa su número de lados, aunque todavía presentan aristas angulosas.
En geología y en el estudio de materiales sedimentarios (donde se trabaja con partículas tridimensionales), se considera que la redondez es la medida de la rugosidad de la superficie, y la forma general se describe mediante la esfericidad.
Definiciones simples

La definición de redondez según la Organización Internacional de Normalización es la relación de los radios de las circunferencias inscrita y circunscrita a una forma dada, es decir, los tamaños máximo y mínimo de las circunferencias que son suficientes para caber dentro y encerrar la forma respectivamente.[1][2]
Diámetro
Tener un diámetro constante, medido en diferentes ángulos alrededor de la forma, a menudo se considera una medida sencilla de la redondez. Sin embargo, es un criterio engañoso.[3]
Aunque el diámetro constante es una condición necesaria para determinar que una forma es circular, no es una condición suficiente: existen formas que tienen un diámetro constante pero están lejos de ser redondas. Formas matemáticas como el triángulo de Reuleaux y, un ejemplo cotidiano, la moneda británica de cincuenta peniques así lo demuestran.
Desplazamientos radiales
La redondez no describe los desplazamientos radiales de una forma desde algún punto central teórico, [nota 1] y simplemente da una idea de su forma general.
Esto es importante en la fabricación de elementos mecánicas como cigüeñales y piezas similares, donde no solo se debe medir la redondez de los cojinetes de deslizamiento, sino también su alineación con respecto a su eje teórico. Un cigüeñal puede tener rodamientos perfectamente redondos, pero si alguno tiene el eje desplazado hacia un lado, el dispositivo no funcionará correctamente. Tales mediciones se realizan a menudo con las mismas técnicas que para la redondez, pero también considerando la posición central y su posición relativa en una dirección axial adicional.
Cálculo en dos dimensiones
Se realiza un recorrido que cubre la rotación completa de la forma, eligiendo puntos perimetrales igualmente espaciados angularmente , en los que se mide el radio , es decir, la distancia entre el centro de rotación y cada punto de la superficie considerado. Un ajuste de mínimos cuadrados a los datos da los siguientes estimadores de los parámetros de redondez:[4]
La desviación se mide entonces como:
Medidas de redondez

La medición de la redondez es muy importante en metrología. Incluye la medición de una colección de puntos.
Métodos
Para ello se siguen dos métodos fundamentales:
Método de referencia intrínseco
- El objeto redondo se coloca sobre una placa plana y el punto de contacto se toma como punto de referencia. Nuevamente, se coloca un indicador de cuadrante sobre el objeto redondo y el objeto se gira manteniendo el punto de referencia en una posición constante. Por lo tanto, el error en la redondez se puede conocer directamente comparando la altura del pico medida por el indicador de cuadrante.
- Alternativamente, se puede usar una base en forma de V en lugar de una placa plana. Existirán dos puntos de referencia en lugar de uno, ya que la base tiene forma de V. El error en la redondez se puede medir de manera similar al método anterior.
- También se puede sujetar un cuerpo cilíndrico entre dos centros de ejes. Aquí también el indicador de cuadrante está montado sobre el cuerpo cilíndrico y, por lo tanto, la redondez se mide mediante un procedimiento similar al anterior.
Método de referencia extrínseco
El método intrínseco se limita solo a pequeñas deformaciones. Para grandes deformaciones se debe seguir el método extrínseco. En este caso, la referencia no es un punto o un conjunto de puntos en el objeto, sino una referencia de precisión separada, generalmente situada en el instrumento de medición. El eje del objeto o parte del objeto a medir está alineado con el eje de rodadura. Luego, se hace que un lápiz óptico del instrumento toque la parte que se va a medir. Un sensor táctil conectado a la punta del lápiz se asegura de que el lápiz toque el objeto. Se toman un mínimo de tres lecturas y se dibuja un gráfico polar amplificado para obtener el error requerido.
Definiciones de error de redondez
- Círculo de mínimos cuadrados (LSC): Es un círculo que separa el perfil de redondez de un objeto al separar la suma de las áreas totales del interior y exterior del mismo en cantidades iguales. El error de redondez se puede estimar entonces como la diferencia entre la distancia máxima y mínima desde este círculo de referencia.
- Círculo de zona mínima (MZC): Aquí se utilizan dos círculos como referencia para medir el error de redondez. Un círculo se dibuja fuera del perfil para encerrarlo en su totalidad y el otro círculo se dibuja dentro del perfil para que solo inscriba el perfil. Ambos círculos, sin embargo, tienen el mismo punto central. El error de redondez aquí es la diferencia entre el radio de los dos círculos.
- Círculo mínimo circunscrito (MCC): Se define como el círculo más pequeño que encierra la totalidad del perfil de redondez. Aquí el error es la desviación más grande con respecto a este círculo.
- Círculo máximo inscrito (MIC): Se define como el círculo más grande que se puede inscribir dentro del perfil de redondez. El error de redondez aquí nuevamente es la desviación máxima del perfil respecto a este círculo inscrito.
- Una definición común utilizada en procesamiento digital de imágenes (análisis de imágenes) para caracterizar formas 2-D es: Redondez= Perímetro24 Π × Área. Esta relación será 1 para un círculo y mayor que 1 para formas no circulares, y es muy similar a la relación isoperimétrica. Otra definición es la inversa: Redondez = 4 Π × ÁreaPerímetro2, que es 1 para un círculo perfecto y desciende hasta 0 para formas altamente no circulares.
Véase también
- Medida de la compacidad de una forma
- Excentricidad, cuánto se desvía una sección cónica (por ejemplo, una elipse) de ser circular
- Achatamiento
- Dimensionamiento geométrico y tolerancia
- Rugosidad (mecánica)
- Esfericidad
Notas
- Aunque muchas máquinas prácticas de medición de redondez se basan en esta técnica de medición, el procesamiento de datos posterior elimina la influencia de la posición del eje.[4]
Referencias
- Organización Internacional de Normalización 1101
- «Introduction to the Measurement of Roundness». Taylor-Hobson Precision. Archivado desde el original el 7 de octubre de 2013. «the separation of two concentric circles that just enclose the circular section of interest. »
- «A guide to the Measurement of Roundness». Taylor-Hobson Precision. «Diameter is not the same as roundness ».
- Medidas de redondez del Instituto Nacional de Estándares y Tecnología