Resistencia inducida

La fuerza aerodinámica total que actúa sobre un cuerpo suele considerarse que tiene dos componentes, la sustentación y la resistencia. Por definición, la componente de la fuerza paralela al flujo que se aproxima se llama resistencia; y la componente perpendicular al flujo que se aproxima se llama sustentación'.[1][2]^{: Section 5.3} En los ángulos de ataque prácticos, la sustentación supera en gran medida a la resistencia.[3]

La sustentación se produce por el cambio de dirección del flujo alrededor de un ala. El cambio de dirección da lugar a un cambio de velocidad (aunque no haya cambio de velocidad), que es una aceleración. Por lo tanto, para cambiar la dirección del flujo es necesario aplicar una fuerza al fluido; la fuerza aerodinámica total es simplemente la fuerza de reacción del fluido que actúa sobre el ala.

Una aeronave en vuelo lento con un ángulo de ataque elevado generará una fuerza de reacción aerodinámica con un alto componente de resistencia. Aumentando la velocidad y reduciendo el ángulo de ataque, la sustentación generada puede mantenerse constante mientras se reduce la componente de resistencia. En el ángulo de ataque óptimo, la resistencia total se minimiza. Si se aumenta la velocidad por encima de este valor, la resistencia total volverá a aumentar debido al incremento del resistencia parásita.

La resistencia inducida provoca vórtices en las puntas de las alas. Cuando se produce la sustentación, el aire por debajo del ala está a una presión mayor que la presión del aire por encima del ala. En un ala de envergadura finita, esta diferencia de presión hace que el aire fluya desde la superficie inferior, alrededor de la punta del ala, hacia la superficie superior.[4]^: 8.1.1 Este flujo de aire en sentido de la envergadura se combina con el aire que fluye en sentido de la cuerda, lo que tuerce el flujo de aire y produce vórtices a lo largo del borde de fuga del ala. La resistencia inducida es la causa de los vórtices; los vórtices no causan la resistencia inducida.[5]^: 4.6

[5]^: 4.7[4]^{: 8.1.4, 8.3, 8.4.1}

Los vórtices reducen la capacidad del ala para generar sustentación, de modo que requiere un mayor ángulo de ataque para la misma sustentación, lo que inclina la fuerza aerodinámica total hacia atrás y aumenta la componente de resistencia de esa fuerza. La desviación angular es pequeña y tiene poco efecto en la sustentación. Sin embargo, se produce un aumento de la resistencia aerodinámica igual al producto de la fuerza de sustentación por el ángulo por el que se desvía. Como la desviación es en sí misma una función de la sustentación, la resistencia adicional es proporcional al cuadrado de la sustentación.[2]^{: Sección 5.17}

Los vórtices creados son inestables, y se combinan rápidamente para producir vórtices de punta de ala que se arrastran detrás de la punta del ala.[2]^{: Sección 5.14}

Para un ala plana con una distribución de sustentación elíptica, la resistencia inducida D_i puede calcularse como sigue:

${\displaystyle D_{\text{i}}={\frac {L^{2}}{{\frac {1}{2}}\rho _{0}V_{E}^{2}\pi b^{2}}}}$,

donde

${\displaystyle L\,}$ es la ascensión,

${\displaystyle \rho _{0}\,}$ es la densidad estándar del aire al nivel del mar,

${\displaystyle V_{E}\,}$ es la velocidad equivalente del aire,

${\displaystyle \pi \,}$ es la relación entre la longitud de una circunferencia y su diámetro, y

${\displaystyle b\,}$ es la envergadura.

De esta ecuación se deduce que la resistencia inducida varía con el cuadrado de la sustentación; e inversamente con el cuadrado de la velocidad aerodinámica equivalente; e inversamente con el cuadrado de la envergadura. Las desviaciones del ala no plana con distribución elíptica de la sustentación se tienen en cuenta dividiendo la resistencia inducida por el factor de eficiencia ${\displaystyle e}$.

Para comparar con otras fuentes de resistencia, puede ser conveniente expresar esta ecuación en términos de coeficientes de elevación y resistencia:[6]

${\displaystyle C_{D,i}={\frac {D_{\text{i}}}{{\frac {1}{2}}\rho _{0}V_{E}^{2}S}}={\frac {C_{L}^{2}}{\pi A\!\!{\text{R}}e}}}$, donde

${\displaystyle C_{L}={\frac {L}{{\frac {1}{2}}\rho _{0}V_{E}^{2}S}}}$

y

${\displaystyle A\!\!{\text{R}}={\frac {b^{2}}{S}}\,}$ es el alargamiento,

${\displaystyle S\,}$ es un área alar de referencia.

Esto indica cómo, para un área de ala dada, las alas de alta relación de aspecto son beneficiosas para la eficiencia del vuelo. Siendo ${\displaystyle C_{L}}$ una función del ángulo de ataque, la resistencia inducida aumenta a medida que aumenta el ángulo de ataque.[2]^{: Section 5.17}

La ecuación anterior puede derivarse utilizando la Teoría de la línea de sustentación de Prandtl.^{[cita requerida]} También se pueden utilizar métodos similares para calcular la mínima resistencia inducida para alas no planas o para distribuciones de sustentación arbitrarias.^{[cita requerida]}

Para un bimotor típico avión de fuselaje ancho a velocidad de crucero, la resistencia inducida es el segundo componente más grande de la resistencia total, representando aproximadamente el 37% de la misma. La resistencia de fricción con la superficie es el mayor componente de la resistencia total, con casi un 48%.[7][8][9]^: 20 Por lo tanto, la reducción de la resistencia inducida puede reducir significativamente el coste y el impacto medioambiental.[9]^: 18

Según las ecuaciones anteriores, para alas que generan la misma sustentación, la resistencia inducida es inversamente proporcional al cuadrado de la envergadura. Un ala de envergadura infinita y segmento del perfil alar uniforme (o un ala 2D) no experimentaría ninguna resistencia inducida.[10] Las características de resistencia de un ala con una envergadura infinita pueden simularse utilizando un segmento aerodinámico del ancho de un túnel de viento.[11]

Un aumento de la envergadura o una solución con un efecto similar es la única manera de reducir la resistencia inducida.[5]^: 4.10 Los hermanos Wright utilizaron bordes de salida curvados en sus alas rectangulares.[12] Algunos de los primeros aviones tenían aletas montadas en las puntas. Los aviones más recientes tienen aletas para reducir la resistencia inducida.[13] Los winglets también proporcionan algún beneficio al aumentar la altura vertical del sistema alar.[5]^: 4.10 Los depósitos de combustible montados en la punta del ala y el giro aerodinámico negativo del ala también pueden proporcionar algún beneficio.^{[cita requerida]}

Normalmente, el ala elíptica produce la mínima resistencia inducida[14] para un ala plana de una envergadura determinada. Un pequeño número de aviones tiene una forma plana que se aproxima a la elíptica - los ejemplos más famosos son el World War II Spitfire[12] y Thunderbolt. Para las alas modernas con winglets, la carga de luz ideal no es elíptica.[5]^: 4.9

Para un área alar determinada, un ala con una alargamiento alta producirá menos resistencia inducida que un ala con una relación de aspecto baja.[15] Mientras que la resistencia inducida es inversamente proporcional al cuadrado de la envergadura, no necesariamente inversamente proporcional a la relación de aspecto, si el área del ala se mantiene constante, entonces la resistencia inducida será inversamente proporcional a la relación de aspecto. Sin embargo, dado que la envergadura puede aumentar mientras disminuye la relación de aspecto, o viceversa, la relación aparente entre la relación de aspecto y la resistencia inducida no siempre se mantiene.[16][4]^: 489

La resistencia total es la resistencia parásita más la resistencia inducida.

En 1891, Samuel Langley publicó los resultados de sus experimentos que mostraban que las placas planas con una mayor alargamiento tenían una mayor sustentación y una menor resistencia aerodinámica.[17] También observó que al viajar a mayor velocidad se utilizaba menos energía,[18] sin embargo sus experimentos sólo se habían realizado a velocidades relativamente bajas.[19] A mayores velocidades, el resistencia parásita llega a dominar, y la potencia requerida aumenta.

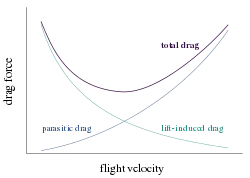
La resistencia inducida debe sumarse a la resistencia parásita para encontrar la resistencia total. Dado que la resistencia inducida es inversamente proporcional al cuadrado de la velocidad aerodinámica (con una determinada sustentación) mientras que la resistencia parásita es proporcional al cuadrado de la velocidad aerodinámica, la curva de resistencia aerodinámica combinada muestra un mínimo a cierta velocidad aerodinámica: la velocidad mínima de resistencia (V_MD). Una aeronave que vuela a esta velocidad está operando a su eficiencia aerodinámica óptima. Según las ecuaciones anteriores, la velocidad para la mínima resistencia se produce a la velocidad en la que la resistencia inducida es igual a la resistencia parásita.[2]^{: Section 5.25} Esta es la velocidad a la que, para un avión sin motor, se alcanza el ángulo de planeo óptimo. Esta es también la velocidad de mayor alcance (aunque la V_MD disminuirá a medida que el avión consuma combustible y sea más ligero). La velocidad para el mayor alcance (es decir, la distancia recorrida) es la velocidad a la que una línea recta desde el origen es tangente a la curva del caudal de combustible.

La curva de autonomía frente a la velocidad del aire es normalmente muy poco profunda y es habitual operar a la 99% de autonomía óptima ya que esto proporciona un 3-5% más de velocidad por sólo un 1% menos de autonomía. Volar más alto, donde el aire es más fino, aumentará la velocidad a la que se produce la mínima resistencia, lo que permite un viaje más rápido con la misma cantidad de combustible. Si el avión vuela a la velocidad máxima permitida, existe una altitud en la que la densidad del aire será suficiente para mantenerlo en el aire mientras vuela con el ángulo de ataque que minimiza la resistencia. La altitud óptima aumentará durante el vuelo a medida que el avión sea más ligero.

• Fuerza aerodinámica
• Resistencia (fluidos)
• Factor de eficiencia de Oswald

• L. J. Clancy (1975), Aerodynamics, Pitman Publishing Limited, London. ISBN 0-273-01120-0
• Abbott, Ira H., and Von Doenhoff, Albert E. (1959), Theory of Wing Sections, Dover Publications, Standard Book Number 486-60586-8
• Luciano Demasi, Antonio Dipace, Giovanni Monegato, and Rauno Cavallaro. Invariant Formulation for the Minimum Induced Drag Conditions of Nonplanar Wing Systems, AIAA Journal, Vol. 52, No. 10 (2014), pp. 2223–2240. doi: 10.2514/1.J052837

• Doug McLean, Common Misconceptions in Aerodynamics en YouTube.