Rotación solar

La tasa de rotación diferencial generalmente se describe mediante la ecuación:

${\displaystyle \omega =A+B\,\sin ^{2}(\varphi )+C\,\sin ^{4}(\varphi )}$

donde ω es la velocidad angular en grados por día, φ es la latitud solar y A, B y C son constantes. Los valores de A, B y C difieren según las técnicas utilizadas para realizar la medición, así como el período de tiempo estudiado.[1]

Un conjunto actual de valores promedio aceptados[2] es:

A = 14.713 ± 0.0491 °/día

B = -2.396 ± 0.188 °/día

C = -1.787 ± 0.253 °/día

En el ecuador, el período de rotación solar es de 24,47 días. Es conocido como el período de rotación sideral, y no debe confundirse con el período de rotación período orbital de 26,24 días, que es el tiempo necesario para que un determinado elemento localizado sobre la superficie del Sol gire a la misma posición aparente vista desde Tierra. El período sinódico es más largo porque el Sol debe rotar durante un período sideral más una cantidad adicional debido al movimiento orbital de la Tierra alrededor del Sol. Téngase en cuenta que la literatura astrofísica no suele utilizar el período de rotación ecuatorial, sino que a menudo utiliza la definición de la rotación de Carrington: un período de rotación sinódica de 27,2753 días (o un período sidéreo de 25,38 días). Este período elegido corresponde aproximadamente a la rotación en una latitud de 26 grados, que es consistente con la latitud típica de las manchas solares y la correspondiente actividad solar periódica. Cuando el Sol es visto desde el "norte" (considerando el polo norte de la Tierra apuntando hacia arriba), la rotación solar es en sentido antihorario. Para una persona situada en el polo norte de la Tierra, las manchas solares parecen moverse de izquierda a derecha a través de la superficie del Sol.

Las constantes de rotación se han medido midiendo el movimiento de varios elementos característicos ("trazadores") de la superficie solar. Los primeros y más usados rastreadores son las manchas solares. Aunque las manchas solares se habían observado desde la antigüedad, solo cuando el telescopio comenzó a usarse se pudo determinar que giraban con el Sol, y así se pudo definir el período de rotación solar. El erudito inglés Thomas Harriot fue probablemente el primero en observar las manchas solares de forma telescópica, como lo demuestra un dibujo en su cuaderno del 8 de diciembre de 1610. Las primeras observaciones publicadas (junio de 1611) tituladas "De Maculis in Sole Observatis, et Apparente earum cum Sole Conversione Narratio"("Narración de los puntos observados en el Sol y su aparente rotación con el Sol") fueron hechas por Johannes Fabricius, que había estado observando sistemáticamente las manchas solares durante algunos meses y también había notado su movimiento a través del disco solar. Esto se puede considerar como la primera evidencia observacional de la rotación solar. Christoph Scheiner ("Rosa Ursine sive solis", libro 4, parte 2, 1630) fue el primero en medir la velocidad de rotación ecuatorial del Sol y notó que la rotación en latitudes más altas es más lenta, por lo que puede considerarse el descubridor de la rotación solar diferencial.

Cada medición da un valor ligeramente diferente, produciendo las desviaciones estándar anteriores (que se muestran como +/-). Saint John (1918) fue quizás el primero en resumir las tasas de rotación solar publicadas hasta entonces, y concluyó que las diferencias en series medidas en diferentes años difícilmente pueden atribuirse a la observación personal o a perturbaciones locales en el Sol, y probablemente se deben a variaciones en la tasa de rotación, y Hubrecht (1915) fue el primero en encontrar que los dos hemisferios solares rotan de manera diferente. Un estudio de datos magnetográficos mostró un período sinódico de acuerdo con otros estudios de 26,24 días en el ecuador y de casi 38 días en los polos.[4]

Rotación interna en el Sol, que muestra la rotación diferencial en la región convectiva externa y una rotación casi uniforme en la región radiativa central. La transición entre estas regiones se llama tacoclina.

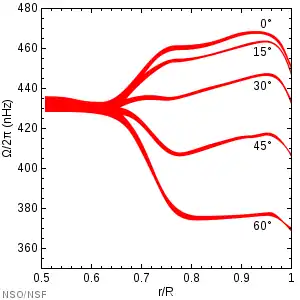
Hasta la aparición de la heliosismología, el estudio de las oscilaciones de las ondas en el Sol, se sabía muy poco acerca de la rotación interna del Sol. Se pensaba que el perfil diferencial de la superficie se extendía al interior del Sol, como discos giratorios de momento angular constante.[5] A través de la heliosismología, ahora se sabe que este no es el caso y se ha encontrado el perfil interno de rotación del Sol. En la superficie, el Sol gira lentamente en los polos y rápidamente en el ecuador. Este perfil se extiende en líneas aproximadamente radiales a través de la zona de convección hacia el interior. En la tacoclina, la rotación cambia bruscamente a rotación de cuerpo sólido en la zona de radiación.[6]

• Rotación diferencial
• Magnetohidrodinámica
• Período orbital
• Tacoclina

• Cox, Arthur N., Ed. "Cantidades Astrofísicas de Allen", 4th Ed, Springer, 1999.
• Javaraiah, J., 2003. Variaciones a largo plazo en la rotación solar diferencial. Solar Phys., 212 (1): 23-49.
• S t. John, C., 1918. La condición actual del problema de la rotación solar, Publicaciones de la Sociedad Astronómica del Pacífico, V.30, No. 178, 318-325.

• Fechas de comienzo de la rotación de Carrington 1853-2016
• Carrington Rotation Start and Stop Times Archivado el 13 de febrero de 2021 en Wayback Machine.
• Carrington Rotation Number