Secreto perfecto
El secreto de un esquema de cifrado se mide como la incertidumbre acerca del mensaje en claro conocido el texto cifrado. Diremos que un criptosistema tiene un secreto perfecto si el conocimiento del texto cifrado no proporciona ninguna información acerca del mensaje en claro salvo, en algunos casos, su longitud. Matemáticamente:
donde:
- representa al texto en claro
- , llamada probabilidad a priori, es la probabilidad de haber recibido un mensaje M. Por tanto
- , llamada probabilidad a posteriori es la probabilidad de haber recibido el mensaje M en tanto se ha recibido un criptograma C.
Si hay secreto perfecto el criptoanálisis es imposible.
Si no hay secreto perfecto el criptosistema puede entregar pistas al criptoanalista. En el sentido de que conocidos algunos textos cifrados es posible descartar algunos posibles mensajes en claro. Observar que puede haber algunos textos cifrado que no aporten información alguna, pero si hay uno que sí permite descartar mensajes en claro.
Caracterización
Usando probabilidades
Para alcanzar el secreto perfecto es condición necesaria y suficiente que para cualquier valor de M se cumpla que la probabilidad de recibir un texto cifrado C en tanto que ha sido enviado el mensaje M cifrado con alguna clave k, sea la misma que la de recibir un criptograma C en tanto se ha enviado un mensaje diferente M' usando otra clave. Matemáticamente:
- donde:
- es la probabilidad de recibir un texto cifrado C en tanto se ha cifrado un mensaje en claro M.
- Por tanto:
- donde k cumple
- es decir, la probabilidad de recibir un criptograma C en tanto se ha enviado un mensaje M será igual a la suma de las probabilidades de las claves que cifran el mensaje M como un texto cifrado C.
- es la probabilidad de recibir un criptograma C. Por tanto
Usando información mutua y entropía
Aprovechando el concepto de información mutua de la Teoría de la información podemos decir[1] que hay secreto perfecto cuando
- como la información mutua se puede calcular a partir de las entropías mediante
- entonces
- Además, se puede demostrar[1] que
- Esto implica que cuando la incertidumbre de un conjunto de claves es pequeño, la información mutua será más grande (en media) y por tanto habrá más independencia entre el texto en plano y el texto cifrado. Además, si suponemos que tenemos secreto perfecto , aplicando la fórmula anterior obtenemos . Esta es la llamada Desigualdad pesimista de Shannon. Si asumimos que cada clave y cada texto plano tiene la misma probabilidad de ocurrencia y por tanto implica que el número de claves sea mayor o igual al conjunto de posibles textos cifrados .
- Por esto se dice que para que un sistema posea secreto perfecto, debe cumplirse que el espacio de las claves aleatorias sea igual o mayor que el espacio de los mensajes. Los cifradores de clave aleatoria de uso único, que se conocen con el nombre genérico de one-time pad o Libreta de un solo uso, cumplen esta condición. Estos sistemas tienen secreto perfecto porque la probabilidad de aplicar cualquier desplazamiento dentro de un rango al elemento i+1 es la misma y además es independiente del desplazamiento aplicado al carácter que le precedía.
Eventos de seguridad
Pudiera parecer que para tener secreto perfecto es necesario , sin embargo esto se puede evitar[1] introduciendo el concepto de eventos de seguridad (en inglés security events) introducidos por Ueli M. Maurer[2] y James L. Massey.[3] Los eventos de seguridad ofrecen una nueva forma de abordar la seguridad de un sistema basándose en herramientas de la Teoría de la información
Ueli M. Maurer define que cuando ocurre un evento de seguridad S, entonces el sistema de secreto es incondicionalmente seguro. Sin embargo si el evento de seguridad S no ocurre, entonces el sistema de seguridad puede no ser seguro. La desigualdad pesimista de Shannon puede ser interpretado con el caso especial donde S sucede y donde el secreto es total. Como ejemplo de este tipo de sistemas Ueli M. Maurer usó el cifrador con seguridad demostrada pero totalmente impracticable de Rip van Winkie.[4] Sin embargo veámoslo aplicado al cifrador de seguridad demostrada pero impracticable de Diffie.
Ejemplo
Considerar una red telefónica con muchos terminales 2L que pueden ser llamados por cualquiera. Cada número de teléfono tiene L bits. Cuando uno llama al teléfono I, éste contesta con un pregrabada secuencia binaria RI de longitud N, con N>>L (y por tanto se puede cumplir H(M)>>H(K)), que es única para cada número de teléfono y que fue obtenida de forma aleatoria. Este valor puede ser conocido por un emisor y un receptor, pero no por un enemigo criptoanalista, pudiendo de este modo funcionar como clave. El sistema funciona de la siguiente forma:
- Cuando uno quiere enviar un mensaje de N-bits de un mensaje en claro M a un receptor, el emisor llama a un número de teléfono K y obtiene una secuencia aleatoria RK.
- El emisor entonces añade RK a M usando y produce un criptograma C de N bits que envía sobre un canal inseguro al receptor.
- El receptor, cuando recibe C, llama al número de teléfono K y obtiene RK. Entonces aplica la operación inversa a la de cifrado y obtiene M
El evento de seguridad de este ejemplo es el hecho de que el criptoanalista que intercepte C e intente recuperar M, no pueda obtener el número secreto K. Si no se tiene K, no se puede llamar al teléfono que nos da la secuencia RK y por tanto RK es completamente impredecible para él. Sin embargo, si el criptoanalista llama accidentalmente a K (lo cual es muy improbable), él puede descifrar C y por tanto el sistema no es fiable. Si el criptoanalista llama a t números de teléfono entonces, la probabilidad de que S no ocurra es
Ejemplos
- Sea un espacio de mensajes , un espacio de claves y un espacio de textos cifrados . Para que se cumpla el secreto perfecto debe cumplirse que la probabilidad de recibir cualquier criptograma sea la misma para cada mensaje con un clave distinta. Por ejemplo tendría secreto perfecto el sistema de cifrado representado por la figura 1.
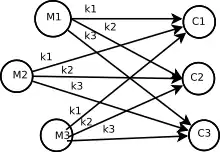 Figura 1: Ejemplo de secreto perfecto.
Figura 1: Ejemplo de secreto perfecto. - Sea un espacio de mensajes , un espacio de claves y un espacio de textos cifrados definidos por la figura 2. Se puede observar que si se ha recibido el criptograma sólo es posible que se deba a la acción de cifrar el mensaje con ó con pero imposible con . Por tanto no hay secreto perfecto.
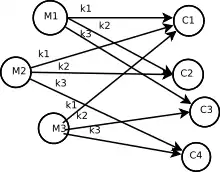 Figura 2: Ejemplo de secreto no perfecto
Figura 2: Ejemplo de secreto no perfecto
Referencias
- Jorge Ramió Aguirre, Aplicaciones criptográficas. Libro guía de la asignatura de Seguridad Informática. Escuela Universitaria de Informática. Universidad Politécnica de Madrid. Enero 1998.
- J.C.A. Lubbe "Basic Methods of Cryptography". Cambridge University Press 1998
- Ueli M. Maurer,"A provably-secure strongly-randomized cipher". Advances in cryptology--EUROCRYPT '90.Springer-Verlag, 1991
- J.L.Massey,"The relevance of information theory to modern cryptography", Institute for Signal and Information Processing.Zurich
- J.L.Massey y I. Ingermarsson,"The Rip van Wikie ciper-a simple anda provably computationally secure cipher", IEEE International Symposion. Brighton 1985