Información mutua

Consideremos dos variables aleatorias X e Y con posibles valores x_i, i=1,2,...,n, y_j, j=1,2,...,m respectivamente. Podemos usar la notación ${\displaystyle P(X=x_{i}|Y=y_{i})=P(x_{i}|y_{j})}$ y ${\displaystyle P(X=x_{i})=P(x_{i})}$

Podemos definir la información mutua ${\displaystyle I(x_{i};y_{j})}$ entre ${\displaystyle x_{i}}$ y ${\displaystyle y_{j}}$ como:[3]

${\displaystyle I(x_{i};y_{j})=\log {\frac {P(x_{i}|y_{j})}{P(x_{i})}}}$

La unidad del concepto está determinado por la base del logaritmo usado. Se suelen usar logaritmos base dos, por tanto, la unidad de medida más común es el bit.

De la propia definición podemos concluir que ${\displaystyle I(x_{i};y_{j})=I(y_{j};x_{i})}$ ya que:

${\displaystyle {\frac {P(x_{i}|y_{j})}{P(x_{i})}}={\frac {P(x_{i}|y_{j})P(y_{j})}{P(x_{i})P(y_{j})}}={\frac {P(x_{i},y_{j})}{P(x_{i})P(y_{j})}}={\frac {P(y_{j}|x_{i})}{P(y_{j})}}}$

La información mutua media mide la información mutua media que se produce entre los distintos valores de dos variables aleatorias. Para ello proporcionamos un peso a los valores de ${\displaystyle I(x_{i};y_{j})}$ sobre la base de la probabilidad de ocurrencia. Por tanto, la información mutua media de dos variables aleatorias discretas X e Y puede definirse como:[3]

${\displaystyle I(X;Y)=\sum _{i=1}^{n}\sum _{j=1}^{m}P(x_{i},y_{j})I(x_{i};y_{j})=\sum _{i=1}^{n}\sum _{j=1}^{m}P(x_{i},y_{j})\log {\frac {P(x_{i}|y_{j})}{P(x_{i})}}=\sum _{i=1}^{n}\sum _{j=1}^{m}P(x_{i},y_{j})\log {\frac {P(x_{i},y_{j})}{P(x_{i})P(y_{j})}}}$

En el caso continuo, reemplazamos la suma con una integral doble definida:

${\displaystyle I(X;Y)=\int _{Y}\int _{X}p(x,y)\log {\left({\frac {p(x,y)}{p(x)\,p(y)}}\right)}\;dx\,dy,}$

Como en el caso de ${\displaystyle I(x_{i};y_{j})}$, la unidad del concepto está determinado por la base del logaritmo usado Se suele usar el logaritmo con base dos y por tanto la unidad más común es el bit.

Relación con entropía

Relación entre entropías e información mutua media[3]

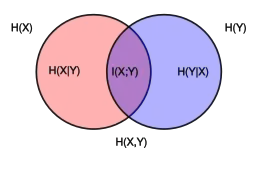
El valor de la información mutua media se puede obtener a partir del concepto de entropía. usando las definiciones matemáticas de las [entropía (información)|entropías]] H(X), H(X,Y) y H(X|Y)

${\displaystyle H(X)=-\sum _{i}p(x_{i})\log _{2}p(x_{i})}$

${\displaystyle H(X,Y)=-\sum _{x,y}p(x,y)\log _{2}p(x,y)}$

${\displaystyle H(X|Y)=-\sum _{y}p(y)\sum _{x}p(x|y)\log _{2}p(x|y)}$

obtenemos

${\displaystyle I(X;Y)=H(X)-H(X|Y)=H(Y)-H(Y|X)}$

De lo anterior y de la propiedad de las entropías

${\displaystyle H(X,Y)=H(X)+H(Y|X)=H(Y)+H(X|Y)}$

obtenemos

${\displaystyle I(X;Y)=H(X)+H(Y)-H(X,Y)}$

Por tanto,

${\displaystyle I(X;X)=H(X)+H(X)-H(X,X)=H(X)}$

lo que indica que la entropía es un tipo especial de información mutua media

• Divergencia de Kullback-Leibler
• Prueba χ² de Pearson