Sexto problema de Hilbert
El sexto problema de Hilbert (uno de los conocidos como veintitrés Problemas de Hilbert, publicados en 1900 por el matemático alemán David Hilbert), plantea la posibilidad de axiomatizar aquellas ramas de la física en las que prevalecen las matemáticas.[2] En su traducción común al español, la declaración explícita dice:
- 6. Tratamiento matemático de los axiomas de la física. Las investigaciones sobre los fundamentos de la geometría plantean el problema: “Tratar de igual manera, por medio de axiomas, aquellas ciencias físicas en las que ya hoy las matemáticas juegan un papel importante; en el primer rango están la teoría de probabilidades y la mecánica".
Hilbert dio una explicación más detallada de este problema y sus posibles formas específicas:
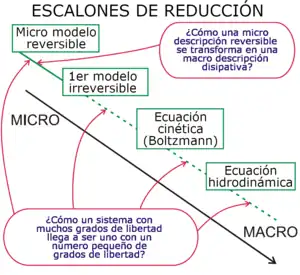
- "En cuanto a los axiomas de la teoría de probabilidades, me parece deseable que su investigación lógica vaya acompañada de un desarrollo riguroso y satisfactorio del método de valores medios en física matemática, y en particular en la teoría cinética de gases. ... El trabajo de Boltzmann sobre los principios de la mecánica sugiere el problema de desarrollar matemáticamente los procesos limitantes, allí simplemente indicados, que conducen desde la visión atomística a las leyes del movimiento de los continuos".
Historia
El mismo David Hilbert dedicó gran parte de su investigación al sexto problema;[3] en particular, trabajó en los campos de la física que surgieron después de plantear el problema.
En la década de 1910, la mecánica celeste se convirtió en la relatividad general. Hilbert y Emmy Noether mantuvieron una gran correspondencia con Albert Einstein en la formulación de la teoría.[4]
En la década de 1920, la mecánica de los sistemas microscópicos evolucionó hacia la mecánica cuántica. Hilbert, con la ayuda de John von Neumann, L. Nordheim y E. P. Wigner, trabajó en la base axiomática de la mecánica cuántica (véase espacio de Hilbert).[5] Al mismo tiempo, pero de forma independiente, Dirac formuló la mecánica cuántica de una manera cercana a un sistema axiomático, como lo hizo Hermann Weyl con la ayuda de Erwin Schrödinger.
En la década de 1930, la teoría de la probabilidad fue puesto sobre una base axiomática por Andréi Kolmogórov, usando la teoría de la medida.
Desde la década de 1960, siguiendo el trabajo de Arthur Wightman y Rudolf Haag, la teoría cuántica de campos moderna también puede considerarse cercana a una descripción axiomática.
En las décadas de 1990 y 2000, el problema de "los procesos limitantes, simplemente indicados, que conducen desde la visión atomista a las leyes del movimiento de los continuos" fue abordado por muchos grupos de matemáticos. Los principales resultados recientes se resumen en el trabajo de Laure Saint-Raymond,[6] Marshall Slemrod,[7] Alexander N. Gorban e Ilya Karlin.[8]
Estado
El sexto problema de Hilbert fue una propuesta para expandir el método axiomático fuera de las disciplinas matemáticas existentes, a la física e incluso más allá. Esta expansión requiere el desarrollo de la semántica de la física con un análisis formal de la noción de realidad física.[9] Dos teorías fundamentales capturan la mayoría de los fenómenos fundamentales de la física:
- La teoría cuántica de campos,[10] que proporciona el marco matemático para el modelo estándar de la física de partículas;
- La relatividad general, que describe el espacio-tiempo y la gravedad a escala macroscópica.
Hilbert consideró la relatividad general como una parte esencial de la base de la física.[11][12] Sin embargo, la teoría cuántica de campos no es lógicamente consistente con la relatividad general, lo que indica la necesidad de una teoría aún desconocida de gravedad cuántica. Por tanto, el sexto problema de Hilbert permanece abierto.[13]
Véase también
Referencias
- Gorban, Alexander N.; Karlin, Ilya V. (2005). Invariant Manifolds for Physical and Chemical Kinetics. Lecture Notes in Physics (LNP, vol. 660). Berlin, Heidelberg: Springer. ISBN 978-3-540-22684-0. doi:10.1007/b98103. Archivado desde el original el 19 de agosto de 2020. Alt URL
- Hilbert, David (1902). «Mathematical Problems». Bulletin of the American Mathematical Society 8 (10): 437-479. MR 1557926. doi:10.1090/S0002-9904-1902-00923-3. Publicaciones anteriores (originales en alemán) aparecieron en el Göttinger Nachrichten, 1900, pp. 253–297, y en el Archiv der Mathematik und Physik, 3ª serie, vol. 1 (1901), pp. 44-63, 213–237.
- Corry, L. (1997). «David Hilbert and the axiomatization of physics (1894–1905)». Archive for History of Exact Sciences 51 (2): 83-198. doi:10.1007/BF00375141.
- Sauer, 1999, p. 6
- van Hove, Léon (1958). «Von Neumann's contributions to quantum theory». Bull. Amer. Math. Soc. 64 (3): 95-99. MR 0092587. Zbl 0080.00416. doi:10.1090/s0002-9904-1958-10206-2.
- Saint-Raymond, L. (2009). Hydrodynamic limits of the Boltzmann equation. Lecture Notes in Mathematics 1971. Springer-Verlag. ISBN 978-3-540-92847-8. doi:10.1007/978-3-540-92847-8.
- Slemrod, M. (2013). «From Boltzmann to Euler: Hilbert's 6th problem revisited». Comput. Math. Appl. 65 (10): 1497-1501. MR 3061719. doi:10.1016/j.camwa.2012.08.016.
- Gorban, A.N.; Karlin, I. (2014). «Hilbert's 6th Problem: exact and approximate hydrodynamic manifolds for kinetic equations». Bull. Amer. Math. Soc. 51 (2): 186-246. arXiv:1310.0406. doi:10.1090/S0273-0979-2013-01439-3.
- Gorban, A.N. (2018). «Hilbert's sixth problem: the endless road to rigour». Phil. Trans. R. Soc. A 376 (2118): 20170238. Bibcode:2018RSPTA.37670238G. PMID 29555808. arXiv:1803.03599. doi:10.1098/rsta.2017.0238.
- Wightman, A.S. (1976). «Hilbert's sixth problem: Mathematical treatment of the axioms of physics». En Felix E. Browder, ed. Mathematical Developments Arising from Hilbert Problems. American Mathematical Society XXVIII. American Mathematical Society. pp. 147-240. ISBN 0-8218-1428-1.
- Hilbert, David (1915). «Die Grundlagen der Physik. (Erste Mitteilung)». Nahrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-physikalische Klasse 1915: 395-407.
- Sauer, 1999
- Theme issue «Hilbert's sixth problem». Phil. Trans. R. Soc. A 376 (2118). 2018. doi:10.1098/rsta/376/2118.
Bibliografía
- Sauer, Tilman (1999). «The relativity of discovery: Hilbert's first note on the foundations of physics». Arch. Hist. Exact Sci. 53 (6): 529-575. Bibcode:1998physics..11050S. Zbl 0926.01004. arXiv:physics/9811050.
- Wightman, A.S. (1976). «Hilbert's sixth problem: Mathematical treatment of the axioms of physics». En Felix E. Browder, ed. Mathematical Developments Arising from Hilbert Problems. American Mathematical Society XXVIII. American Mathematical Society. pp. 147-240. ISBN 0-8218-1428-1.