Subconjunto

$A$ es subconjunto de otro conjunto $B$ si todos los elementos de $A$ pertenecen también a $B$ . Decimos entonces que $A$ «está contenido» dentro de $B$ .

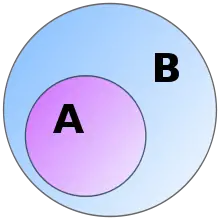
Diagrama de Euler mostrando que A es un subconjunto de B.
Es decir, A ⊆ B.

Definición

La diferencia entre los conjuntos es formado por elementos que pertenecen a uno y a los otros no.
Otras maneras de decirlo son « $A$ está incluido en $B$ », « $B$ incluye a $A$ »,etc.

Ejemplos

El «conjunto de todas las mujeres» es un subconjunto del «conjunto de todas las personas».
${1, 3} \subseteq {1, 2, 3, 4$ }
${2, 4, 6,...} \subseteq {1, 2, 3,..} = N$ . Es decir, números pares ⊆ números naturales

Subconjunto propio

Es cierto que cada elemento de un conjunto $A$ es un elemento de $A$ (es una afirmación tautológica). Por tanto se tiene el siguiente teorema:

Todo conjunto $A$ es subconjunto de sí mismo.

Así, dados dos conjuntos $A \subseteq B$ , cabe la posibilidad de que sean iguales, $A = B$ .

Por otro lado, es posible también que $A$ contenga algunos pero no todos los elementos de $B$ :

Sea $A$ un subconjunto de $B$ tal que $A \neq B$ . Entonces se dice que $A$ es un subconjunto propio de $B$ , y se denota por $A ⊊ B$ .
(A su vez, se dice que $B$ es un superconjunto propio de $A$ , $B ⊋ A$ )

Es verdadero que todos los ejemplos de subconjunto mostrados arriba son de hecho subconjuntos propios.

También se utiliza la notación $A \subset B$ y $B \supset A$ , pero según el autor esto puede denotar subconjunto, $A \subseteq B$ y $B \supseteq A$ ; o subconjunto propio, $A ⊊ B$ y $B ⊋ A$ .[1]

Conjunto potencia

La totalidad de los subconjuntos de un conjunto dado $A$ constituye el llamado conjunto potencia o conjunto partes de $A$ :

El conjunto potencia de $A$ es el conjunto formado por todos los subconjuntos de $A$ :

${\mathcal {P}}(A)=\{B:\,B\subseteq A\}$

Cuando el conjunto $A$ tiene un número finito de elementos, por ejemplo $| A | = n$ , el conjunto potencia también es finito y tiene $2 n$ elementos.

Por ejemplo, dado el conjunto $A = {a, b}$ , su conjunto potencia es:

{\mathcal {P}}(A)=\{\emptyset ,\,\{a\},\,\{b\},\,\{a,b\}\}

Propiedades

El conjunto vacío, denotado como $\emptyset$ , es subconjunto de cualquier conjunto.

Esto es debido a que «todo elemento de $\emptyset$ lo es de $A$ » significa lo mismo que « $\emptyset$ no tiene ningún elemento que esté en $A$ », y esto es cierto sea cual sea $A$ ya que $\emptyset$ no tiene elementos.

Si cada elemento de un conjunto $A$ lo es de otro conjunto $B$ , y cada elemento de $B$ a su vez lo es de otro conjunto $C$ , entonces cada miembro de $A$ pertenece también a $C$ , o sea:

A\subseteq B

y

B\subseteq C

implica

A\subseteq C.

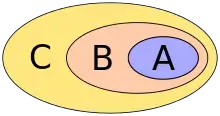
En el diagrama,

A\subseteq B\subseteq C

.

Dados tres conjuntos $A$ , $B$ y $C$ , si $A$ es subconjunto de $B$ y $B$ es subconjunto de $C$ , entonces $A$ es subconjunto de $C$ .

Además, si dos conjuntos son subconjuntos el uno del otro, entonces todos los miembros de uno lo son del otro y viceversa. Entonces, ambos conjuntos poseen los mismos elementos, y los conjuntos quedan definidos únicamente por sus elementos, luego:

Si $A$ es subconjunto de $B$ y $B$ es subconjunto de $A$ , entonces $A = B$ .

Propiedades avanzadas

La relación de inclusión tiene las mismas propiedades que la relación de orden no estricto: es reflexiva ( $A \subseteq A$ ); transitiva ( $A \subseteq B$ y $B \subseteq C$ implican $A \subseteq C$ ); y antisimétrica ( $A \subset B$ y $B \subset A$ implican $A = B$ ).

Bibliografía

Lipschutz, Seymour (1991). Teoría de conjuntos y temas afines. McGraw-Hill. ISBN 968-422-926-7.

Véase también

Referencias

Lipschutz, 1991, p. 3.

Enlaces externos

Esta obra contiene una traducción derivada de «Subset» de Wikipedia en inglés, publicada por sus editores bajo la Licencia de documentación libre de GNU y la Licencia Creative Commons Atribución-CompartirIgual 4.0 Internacional.

Datos: Q177646
Multimedia: Subsets / Q177646

Este artículo ha sido escrito por Wikipedia. El texto está disponible bajo la licencia Creative Commons - Atribución - CompartirIgual. Pueden aplicarse cláusulas adicionales a los archivos multimedia.

[1] Lipschutz, 1991, p. 3.