Sustitución de Weierstrass
En cálculo integral, la sustitución de Weierstrass, sustitución por la tangente del ángulo mitad o cambio de variable universal es un método para evaluar primitivas, que convierte una función racional de funciones trigonométricas de en una función racional ordinaria de al hacer el cambio de variable .[1][2] sin pérdida de generalidad, tomando estas como funciones racionales del seno y del coseno. La fórmula de transformación general es
Lleva el nombre de Karl Weierstraß (1815-1897),[3][4][5] aunque se puede encontrar en un libro de Leonhard Euler de 1768.[6] Michael Spivak escribió que este método era la "sustitución más ingeniosa" del mundo.[7]
La sustitución
Se comienza con una integral en la que el integrando es una función racional que contiene las funciones trigonométricas y/o , esta integral se transforma en una integral sin funciones trigonométricas mediante un cambio de variable.
Por lo tanto,
Deducción de las fórmulas
Por las identidades y fórmulas de trigonometría,
y
Finalmente, si entonces
Por lo tanto
Ejemplos
Primer ejemplo: integral de la cosecante
Se puede confirmar el resultado anterior usando un método estándar para evaluar la integral de la cosecante multiplicando el numerador y el denominador por y realizando el siguiente cambio de variable
Por lo que
Ahora, las fórmulas del ángulo mitad para senos y cosenos son
respectivamente y permiten obtener
por lo que los dos resultados son equivalentes. La expresión
es una de las fórmulas de la tangente del ángulo mitad. La integral de la secante puede evaluarse de manera similar.
Segundo ejemplo: una integral definida
En la primera línea, no se sustituye simplemente por ambos límites de integración. Se debe tener en cuenta la singularidad (en este caso, una asíntota vertical) de en . Alternativamente, primero se debe evaluar la integral indefinida y luego aplicar los valores del intervalo.
Por simetría,
que es igual al resultado anterior.
Tercer ejemplo: seno y coseno
Si
Geometría

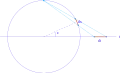
A medida que varía x, el punto (cos x, sin x) se arrolla repetidamente alrededor de la circunferencia goniométrica centrada en (0, 0). El punto
da una sola vuelta a la circunferencia, ya que t recorre de −∞a +∞, y nunca alcanza el punto (−1, 0), que se aproxima como un límite cuando t se acerca a ±∞. Como t recorre desde −∞ a −1, el punto determinado por t pasa por la parte de la circunferencia en el tercer cuadrante, desde (−1, 0) a (0, −1). A medida que t va de −1 a 0, el punto sigue la parte de la circunferencia en el cuarto cuadrante desde (0, −1) a (1, 0). A medida que t va de 0 a 1, el punto sigue la parte de la circunferencia en el primer cuadrante desde (1, 0) hasta (0, 1). Finalmente, cuando t va de 1 a +∞, el punto sigue la parte de la circunferencia en el segundo cuadrante desde (0, 1) a (−1, 0).
También existe otro punto de vista geométrico. Para ello, se debe dibujar el círculo unitario y hacer que P sea el punto (−1, 0). Una recta que pasa por P (excepto la línea vertical) está determinada por su pendiente. Además, cada una de las líneas rectas (excepto la vertical) se cruza con el círculo unitario en exactamente dos puntos, uno de los cuales es P. Esto determina una función que relaciona los puntos en el círculo unitario con las pendientes de las rectas que pasan por ellos. Las funciones trigonométricas determinan una función de ángulos a puntos en el círculo unitario, y al combinar estas dos funciones se obtiene una nueva función que relaciona ángulos y pendientes.
Galería
Funciones hiperbólicas
Al igual que con otras propiedades compartidas entre las funciones trigonométricas y las funciones hiperbólicas, es posible usar las identidades hiperbólicas para construir una forma similar de sustitución:
Véase también
 Portal:Matemáticas. Contenido relacionado con Matemáticas.
Portal:Matemáticas. Contenido relacionado con Matemáticas.- Curva algebraica
- Proyección estereográfica
- Fórmulas de la tangente del ángulo mitad
- Sustitución trigonometrica
- Sustitución de Euler
Lecturas relacionadas
- Edwards, Joseph (1921). «Chapter VI». A Treatise on the Integral Calculus with Applications, Examples, and Problems. London: Macmillan and Co, Ltd.
Referencias
- Stewart, James (2012). Calculus: Early Transcendentals (7th edición). Belmont, CA, USA: Cengage Learning. pp. 493. ISBN 978-0-538-49790-9.
- Weisstein, Eric W. "Weierstrass Substitution." From MathWorld--A Wolfram Web Resource. Accessed April 1, 2020.
- Gerald L. Bradley and Karl J. Smith, Calculus, Prentice Hall, 1995, pages 462, 465, 466
- Christof Teuscher, Alan Turing: Life and Legacy of a Great Thinker, Springer, 2004, pages 105–6
- James Stewart, Calculus: Early Transcendentals, Brooks/Cole, Apr 1, 1991, page 436
- Euler, Leonard (1768). «Institutiionum calculi integralis volumen primum. E342, Caput V, paragraph 261». Euler Archive. Mathematical Association of America (MAA). Consultado el 1 de abril de 2020.
- Michael Spivak, Calculus, Cambridge University Press, 2006, pages 382–383.
- James Stewart, Calculus: Early Transcendentals, Brooks/Cole, 1991, page 439