Tabla de multiplicar

Las tablas de multiplicar se usa para definir la relación del producto entre dos números, según la reglas de la aritmética. Según la correspondencia matemática:

{\displaystyle {\begin{array}{rccl}\ast

Tabla de multiplicar del 1 al 10 dibujada a escala con la mitad superior derecha etiquetada con factorizaciones de primos.

de modo que a cada par ordenado (a,b) de números naturales se le asocia un tercer natural c, que es el producto de los dos primeros.

Las tablas de multiplicar se aprenden en los colegios mediante la memorización[1] de los productos de un número entre 1 y 10 por los sucesivos números entre 0 y 10.

Conocida esta tabla y por el Algoritmo de multiplicación, se pueden realizar multiplicaciones de cualquier número de cifras, incluso aunque estas cifras tengan parte decimal.

La tabla de multiplicar decimal se enseñaba tradicionalmente como parte esencial de la aritmética elemental en todo el mundo, ya que sienta las bases para las operaciones aritméticas con números de base diez. Muchos educadores creen que es necesario memorizar la tabla hasta 9 × 9.[2]

Historia

Época premoderna

The Tsinghua Bamboo Slips, Chinese Warring States era decimal multiplication table of 305 BC

Las tablas de multiplicar más antiguas que se conocen fueron utilizadas por los babilonios hace unos 4000 años.[3] Sin embargo, utilizaban una base de 60.[3] Las tablas más antiguas conocidas que utilizan una base de 10 son las chinas tabla de multiplicación decimal en tiras de bambú que datan de alrededor del 305 a. C., durante el período de los Estados Combatientes de China.[3]

"Tabla de Pitágoras" en huesos de Napier[4]

La tabla de multiplicar se atribuye a veces al antiguo matemático griego Pitágoras (570-495 a. C.). También se llama la Tabla de Pitágoras en muchos idiomas (por ejemplo, francés, italiano y ruso), a veces en inglés.[5] El matemático grecorromano Nicómaco (60-120 d. C.), seguidor del neopitagorismo, incluyó una tabla de multiplicar en su Introducción a la aritmética, mientras que la tabla de multiplicar más antigua que se conserva de las griegas se encuentra en una tablilla de cera datada en el siglo I d. C. y que actualmente se conserva en el Museo Británico.[6]

En 493 d. C., Victorio de Aquitania escribió una tabla de multiplicar de 98 columnas que daba (en números romanos) el producto de cada número de 2 a 50 veces y las filas eran "una lista de números empezando por mil, descendiendo por centenas hasta cien, luego descendiendo por decenas hasta diez, luego por unidades hasta uno, y luego las fracciones hasta 1/144."[7]

Época moderna

En su libro de 1820 La filosofía de la aritmética,[8] el matemático John Leslie publicó una tabla de multiplicar hasta 99 × 99, que permite multiplicar números de dos en dos. Leslie también recomendaba que los alumnos memorizaran la tabla de multiplicar hasta 50 × 50.

La siguiente ilustración muestra una tabla de hasta 12 × 12, que es un tamaño que se utiliza habitualmente hoy en día en las escuelas del mundo anglosajón.

×	1	2	3	4	5	6	7	8	9	10	11	12
0	0	0	0	0	0	0	0	0	0	0	0	0
1	1	2	3	4	5	6	7	8	9	10	11	12
2	2	4	6	8	10	12	14	16	18	20	22	24
3	3	6	9	12	15	18	21	24	27	30	33	36
4	4	8	12	16	20	24	28	32	36	40	44	48
5	5	10	15	20	25	30	35	40	45	50	55	60
6	6	12	18	24	30	36	42	48	54	60	66	72
7	7	14	21	28	35	42	49	56	63	70	77	84
8	8	16	24	32	40	48	56	64	72	80	88	96
9	9	18	27	36	45	54	63	72	81	90	99	108
10	10	20	30	40	50	60	70	80	90	100	110	120
11	11	22	33	44	55	66	77	88	99	110	121	132
12	12	24	36	48	60	72	84	96	108	120	132	144

En China, sin embargo, como la multiplicación de números enteros es conmutativa, muchas escuelas utilizan una tabla más pequeña como la siguiente. Algunas escuelas incluso eliminan la primera columna, ya que 1 es la identidad multiplicativa.

1	1
2	2	4
3	3	6	9
4	4	8	12	16
5	5	10	15	20	25
6	6	12	18	24	30	36
7	7	14	21	28	35	42	49
8	8	16	24	32	40	48	56	64
9	9	18	27	36	45	54	63	72	81
×	1	2	3	4	5	6	7	8	9

El aprendizaje memorístico tradicional de la multiplicación se basaba en la memorización de las columnas de la tabla, de una forma como

1 × 10 = 10
2 × 10 = 20
3 × 10 = 30
4 × 10 = 40
5 × 10 = 50
6 × 10 = 60
7 × 10 = 70
8 × 10 = 80
9 × 10 = 90

|}

Esta forma de escribir la tabla de multiplicar en columnas con frases numéricas completas todavía se utiliza en algunos países, como Bosnia y Herzegovina, en lugar de las modernas cuadrículas anteriores.

Tablas de multiplicar

La forma tradicional de representar la tabla de multiplicar para su memorización o repaso, como su propio nombre indica en forma de tabla.[9][10][11] Donde se multiplica, del uno al diez o del cero al diez, cada uno de los números en la tabla.

{\begin{array}{c}tabla\;de\;multiplicar\\\\{\begin{array}{ccccc}{\begin{array}{|c|}\hline tabla\;del\;1\\{\begin{array}{rcrcr}1&\times &0&=&0\\1&\times &1&=&1\\1&\times &2&=&2\\1&\times &3&=&3\\1&\times &4&=&4\\1&\times &5&=&5\\1&\times &6&=&6\\1&\times &7&=&7\\1&\times &8&=&8\\1&\times &9&=&9\\1&\times &10&=&10\\\end{array}}\\\hline \end{array}}&{\begin{array}{|c|}\hline tabla\;del\;2\\{\begin{array}{rcrcr}2&\times &0&=&0\\2&\times &1&=&2\\2&\times &2&=&4\\2&\times &3&=&6\\2&\times &4&=&8\\2&\times &5&=&10\\2&\times &6&=&12\\2&\times &7&=&14\\2&\times &8&=&16\\2&\times &9&=&18\\2&\times &10&=&20\\\end{array}}\\\hline \end{array}}&{\begin{array}{|c|}\hline tabla\;del\;3\\{\begin{array}{rcrcr}3&\times &0&=&0\\3&\times &1&=&3\\3&\times &2&=&6\\3&\times &3&=&9\\3&\times &4&=&12\\3&\times &5&=&15\\3&\times &6&=&18\\3&\times &7&=&21\\3&\times &8&=&24\\3&\times &9&=&27\\3&\times &10&=&30\\\end{array}}\\\hline \end{array}}\\\\{\begin{array}{|c|}\hline tabla\;del\;4\\{\begin{array}{rcrcr}4&\times &0&=&0\\4&\times &1&=&4\\4&\times &2&=&8\\4&\times &3&=&12\\4&\times &4&=&16\\4&\times &5&=&20\\4&\times &6&=&24\\4&\times &7&=&28\\4&\times &8&=&32\\4&\times &9&=&36\\4&\times &10&=&40\\\end{array}}\\\hline \end{array}}&{\begin{array}{|c|}\hline tabla\;del\;5\\{\begin{array}{rcrcr}5&\times &0&=&0\\5&\times &1&=&5\\5&\times &2&=&10\\5&\times &3&=&15\\5&\times &4&=&20\\5&\times &5&=&25\\5&\times &6&=&30\\5&\times &7&=&35\\5&\times &8&=&40\\5&\times &9&=&45\\5&\times &10&=&50\\\end{array}}\\\hline \end{array}}&{\begin{array}{|c|}\hline tabla\;del\;6\\{\begin{array}{rcrcr}6&\times &0&=&0\\6&\times &1&=&6\\6&\times &2&=&12\\6&\times &3&=&18\\6&\times &4&=&24\\6&\times &5&=&30\\6&\times &6&=&36\\6&\times &7&=&42\\6&\times &8&=&48\\6&\times &9&=&54\\6&\times &10&=&60\\\end{array}}\\\hline \end{array}}\\\\{\begin{array}{|c|}\hline tabla\;del\;7\\{\begin{array}{rcrcr}7&\times &0&=&0\\7&\times &1&=&7\\7&\times &2&=&14\\7&\times &3&=&21\\7&\times &4&=&28\\7&\times &5&=&35\\7&\times &6&=&42\\7&\times &7&=&49\\7&\times &8&=&56\\7&\times &9&=&63\\7&\times &10&=&70\\\end{array}}\\\hline \end{array}}&{\begin{array}{|c|}\hline tabla\;del\;8\\{\begin{array}{rcrcr}8&\times &0&=&0\\8&\times &1&=&8\\8&\times &2&=&16\\8&\times &3&=&24\\8&\times &4&=&32\\8&\times &5&=&40\\8&\times &6&=&48\\8&\times &7&=&56\\8&\times &8&=&64\\8&\times &9&=&72\\8&\times &10&=&80\\\end{array}}\\\hline \end{array}}&{\begin{array}{|c|}\hline tabla\;del\;9\\{\begin{array}{rcrcr}9&\times &0&=&0\\9&\times &1&=&9\\9&\times &2&=&18\\9&\times &3&=&27\\9&\times &4&=&36\\9&\times &5&=&45\\9&\times &6&=&54\\9&\times &7&=&63\\9&\times &8&=&72\\9&\times &9&=&81\\9&\times &10&=&90\\\end{array}}\\\hline \end{array}}\\\end{array}}\\\end{array}}

La tabla de multiplicar por coordenadas de la tabla pitagórica

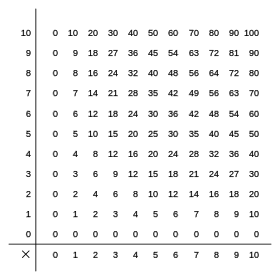
Otra forma de representar la tabla de multiplicar, es la denominada tabla pitagórica[12] (denominada así en honor de Pitágoras), compuesta por coordenadas cartesianas (denominadas así en honor de Descartes). La primera fila y la primera columna contienen los números que se van a multiplicar (habitualmente, los números enteros hasta el 10), y en la intersección de cada fila y cada columna está el producto del número de su fila por el número de su columna.

Esta representación de la tabla de multiplicar es más compacta que la Nueva , y permite ver algunas propiedades de la multiplicación, la propiedad conmutativa, el orden de los factores no altera el producto, por ejemplo el 5·3 es igual a 3·5, esto hace que este cuadro sea una matriz simétrica, los valores situados a un lado otro de la diagonal que une el 1 y el 100, son iguales.

Esta simetría se puede ver también al comprobar que las filas y las columnas de un mismo número son iguales, si vemos la fila del tres, presenta la secuencia: 3, 6, 9, 12..., y si miramos la columna del tres tenemos la misma secuencia 3, 6, 9..., es decir, si cambiamos las filas por las columnas la tabla no varía, esto se debe a la propiedad conmutativa de la multiplicación.

La diagonal principal, recoge los cuadrados de los números, en esta diagonal la fila es igual a la columna, por lo que tenemos que:

a\cdot a=a^{2}\,

La distribución de los números a un lado y otro de esta diagonal también es simétrica según nos alejamos de ella.

Otras tablas de multiplicar

Ábaco neperiano.

Para ejercitar el cálculo mental, algunos aprenden las tablas de multiplicar de números superiores a 10.

En el antiguo Egipto se utilizaba el método de multiplicación por duplicación, que no requiere el aprendizaje de tablas de multiplicar, solo se necesitaba saber sumar para obtener el resultado de multiplicaciones y divisiones.

En la antigua Babilonia, se empleaba un sistema sexagesimal. Se empleaban profusamente tablillas con el producto de un determinado número, no necesariamente entero, por 2,3,4..., hasta 60.

También se emplean tablas de multiplicar en matemáticas más avanzadas, para definir operaciones binarias en sistemas algebraicos como grupos, cuerpo y anillos. Para un ejemplo, véase octoniones.

Otra alternativa son las tablas de multiplicar aprovechando simetrías [13] que sólo necesita memorizar unas pocas cifras y unas pocas posiciones.

Actualmente existen métodos matemáticos sintetizados que permiten aprender las tablas de multiplicar[14] de una forma más sencilla y amigable para el estudiante. De este modo se reducen el número de valores a memorizar, de 80 a 20, lo que facilita la agilidad en el aprendizaje pasando en poco tiempo al refuerzo.

Véase también

Referencias

Coto, Alberto (2009). Ayuda a tu hijo a entrenar su inteligencia (1 edición). Editorial EDAF S.L. p. 61. ISBN 978-84-414-2099-1.
Trivett, John (1980), «La tabla de multiplicar: To Be Memorized or Mastered!», For the Learning of Mathematics 1 (1): 21-25, JSTOR 40247697..
Qiu, Jane (7 de enero de 2014). «Antigua tabla de multiplicar oculta en tiras de bambú chinas». Nature News. S2CID 130132289.
Wikisource:Page:Popular Science Monthly Volume 26.djvu/467
por ejemplo en Tratado elemental de aritmética de John Farrar
David E. Smith (1958), History of Mathematics, Volume I: General Survey of the History of Elementary Mathematics. Nueva York: Dover Publications (reimpresión de la publicación de 1951), ISBN 0-486-20429-4, pp. 58, 129.
David W. Maher y John F. Makowski. "Evidencia literaria de la aritmética romana con fracciones". Classical Philology, 96/4 (octubre de 2001), p. 383.
Leslie, John (1820). La filosofía de la aritmética; Exhibiting a Progressive View of the Theory and Practice of Calculation, with Tables for the Multiplication of Numbers as Far as One Thousand. Edinburgh: Abernethy & Walker.
de Eguilaz, Eugenio (1840). Antonio Mateis Muñoz, ed. Tablas de sumar, restar, multiplicar y dividir (1 edición). p. 12.
Oriol y Bernadet, José (1845). José Matas, ed. Manual de aritmética demostrada: Al alcance de los niños (1 edición). p. 24.
Coto, Alberto (2009). Ayuda a tu hijo a entrenar su inteligencia (1 edición). Editorial EDAF S.L. p. 62. ISBN 978-84-414-2099-1.
Tapia Felipe, Yolanda; García Anaya, Fernando José (2005). Matemáticas 2 (1 edición). Editorial Progreso SA. p. 104. ISBN 970-641-554-8.
«Las tablas de multiplicar por simetrías». 8 de octubre de 2019.
«La nueva tabla de multiplicar». 24 de julio de 2013.

Enlaces externos

Tablas de Multiplicar del 1 al 100
Juegos de Tablas de Multiplicar
Tablas de multiplicar
Tablas de multiplicar para rellenar
Tablas de multiplicar por tiempo
Tablas de Multiplicar para Imprimir
Nuevas tablas de multiplicar
aplicación android para aprender las tablas
Vídeo con truco para recordar fácilmente la tabla del 9 Archivado el 29 de agosto de 2016 en Wayback Machine.

Datos: Q206049
Multimedia: Multiplication tables / Q206049

Este artículo ha sido escrito por Wikipedia. El texto está disponible bajo la licencia Creative Commons - Atribución - CompartirIgual. Pueden aplicarse cláusulas adicionales a los archivos multimedia.

[1] Coto, Alberto (2009). Ayuda a tu hijo a entrenar su inteligencia (1 edición). Editorial EDAF S.L. p. 61. ISBN 978-84-414-2099-1.

[2] Trivett, John (1980), «La tabla de multiplicar: To Be Memorized or Mastered!», For the Learning of Mathematics 1 (1): 21-25, JSTOR 40247697..

[Qiu-3] Qiu, Jane (7 de enero de 2014). «Antigua tabla de multiplicar oculta en tiras de bambú chinas». Nature News. S2CID 130132289.

[4] Wikisource:Page:Popular Science Monthly Volume 26.djvu/467

[5] r ejemplo en Tratado elemental de aritmética de John Farrar

[6] David E. Smith (1958), History of Mathematics, Volume I: General Survey of the History of Elementary Mathematics. Nueva York: Dover Publications (reimpresión de la publicación de 1951), ISBN 0-486-20429-4, pp. 58, 129.

[7] David W. Maher y John F. Makowski. "Evidencia literaria de la aritmética romana con fracciones". Classical Philology, 96/4 (octubre de 2001), p. 383.

[8] Leslie, John (1820). La filosofía de la aritmética; Exhibiting a Progressive View of the Theory and Practice of Calculation, with Tables for the Multiplication of Numbers as Far as One Thousand. Edinburgh: Abernethy & Walker.

[9] Eguilaz, Eugenio (1840). Antonio Mateis Muñoz, ed. Tablas de sumar, restar, multiplicar y dividir (1 edición). p. 12.

[10] Oriol y Bernadet, José (1845). José Matas, ed. Manual de aritmética demostrada: Al alcance de los niños (1 edición). p. 24.

[11] Coto, Alberto (2009). Ayuda a tu hijo a entrenar su inteligencia (1 edición). Editorial EDAF S.L. p. 62. ISBN 978-84-414-2099-1.

[12] Tapia Felipe, Yolanda; García Anaya, Fernando José (2005). Matemáticas 2 (1 edición). Editorial Progreso SA. p. 104. ISBN 970-641-554-8.

[13] «Las tablas de multiplicar por simetrías». 8 de octubre de 2019.

[14] «La nueva tabla de multiplicar». 24 de julio de 2013.