Tabla normal estándar
Una tabla normal estándar, también llamada tabla normal unitaria o tabla Z,[1] es una tabla matemática de los valores de Φ, la función de distribución acumulativa de la distribución normal. Se utiliza para determinar la probabilidad de que se observe una muestra estadística por debajo, por encima o entre dos valores dados de una distribución normal estándar, y por extensión, de cualquier distribución normal. Teniendo en consideración que las tablas de probabilidad no se pueden imprimir para cada distribución normal, dado que existe una variedad infinita de distribuciones normales, es una práctica común convertir una distribución normal en una normal estándar y luego usar la tabla normal estándar para determinar las probabilidades buscadas.[2]
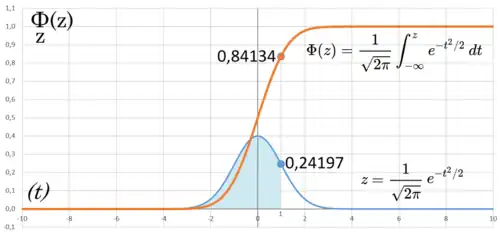
Distribuciones normal y normal estándar
Las distribuciones normales son un tipo de distribuciones simétricas en forma de campana, que son útiles para describir datos del mundo real. La distribución normal estándar, representada por la letra Z, es una distribución normal que tiene una media de 0 y una desviación estándar de 1.
Conversión
Si X es una variable aleatoria de una distribución normal con media μ y desviación estándar σ, su valor asignado Z puede calcularse a partir de X restándole μ y dividiendo por la desviación estándar:
Para el promedio de una muestra de tamaño n de alguna población en la que la media es μ y la desviación estándar es σ, el error estándar es σ/√n:
Manejo de la tabla de Z
Formato / diseño
Las tablas de Z se componen típicamente de la siguiente manera:
- La etiqueta de las filas contiene la parte entera y el primer decimal de Z.
- La etiqueta de las columnas contiene el segundo decimal de Z.
- Los valores dentro de la tabla son las probabilidades correspondientes al tipo de tabla. Estas probabilidades se corresponden con el área bajo la curva normal desde el origen considerado (el 0 para el acumulado desde la media; el infinito negativo para el acumulado de Z; y el infinito positivo para el acumulado complementario de Z).
Ejemplo: para encontrar 0.69, se busca hacia abajo en las filas hasta encontrar 0.6 y luego a través de las columnas hasta 0.09, lo que daría una probabilidad de 0.25490 para una tabla acumulativa desde la media; o 0.75490 para una tabla acumulativa .
Debido a que la curva de distribución normal es simétrica, habitualmente se dan las probabilidades para solo valores positivos de Z. El usuario tiene que usar una operación complementaria con el valor absoluto de Z, como en el ejemplo incluido a continuación.
Tipos de tablas
Las tablas Z usan al menos tres convenciones diferentes:
- Acumulados desde la media
- Se indica la probabilidad de que una estadística esté entre 0 (media) y Z. Ejemplo: Prob (0≤Z≤0,69) = 0.2549
- Acumulados
- Se indica la probabilidad de que un valor estadístico sea menor que Z. Esto equivale al área de la distribución normal de los valores menores que Z. Ejemplo: Prob (Z≤0,69) = 0.7549.
- Acumulados complementarios
- Se especifica la probabilidad de que un valor estadístico sea mayor que Z. Esto equivale al área de la distribución normal correspondiente a los valores mayores que Z.
- Ejemplo: Hallar la probabilidad de que (Z ≥ 0,69). Como esta es la porción del área por encima de Z, la proporción que es mayor que Z se encuentra restando Z de 1. Eso es Prob (Z ≥ 0.69) = 1 - Prob (Z ≤ 0.69) o Prob (Z ≥ 0.69) = 1 - 0.7549 = 0.2451.
Ejemplos con tablas
Acumulado desde la media (0 a Z)

Esta tabla da la probabilidad de que un suceso estadístico esté entre 0 (la media) y Z.
Téngase en cuenta que para z = 1, 2, 3, se obtienen (después de multiplicar por 2 para tener en cuenta el intervalo [-z, z]) los resultados f (z) = 0.6827, 0.9545, 0.9974, característicos de la regla 68-95-99.7.
| z | +0.00 | +0.01 | +0.02 | +0.03 | +0.04 | +0.05 | +0.06 | +0.07 | +0.08 | +0.09 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.0 | 0.00000 | 0.00399 | 0.00798 | 0.01197 | 0.01595 | 0.01994 | 0.02392 | 0.02790 | 0.03188 | 0.03586 |
| 0.1 | 0.03983 | 0.04380 | 0.04776 | 0.05172 | 0.05567 | 0.05962 | 0.06356 | 0.06749 | 0.07142 | 0.07535 |
| 0.2 | 0.07926 | 0.08317 | 0.08706 | 0.09095 | 0.09483 | 0.09871 | 0.10257 | 0.10642 | 0.11026 | 0.11409 |
| 0.3 | 0.11791 | 0.12172 | 0.12552 | 0.12930 | 0.13307 | 0.13683 | 0.14058 | 0.14431 | 0.14803 | 0.15173 |
| 0.4 | 0.15542 | 0.15910 | 0.16276 | 0.16640 | 0.17003 | 0.17364 | 0.17724 | 0.18082 | 0.18439 | 0.18793 |
| 0.5 | 0.19146 | 0.19497 | 0.19847 | 0.20194 | 0.20540 | 0.20884 | 0.21226 | 0.21566 | 0.21904 | 0.22240 |
| 0.6 | 0.22575 | 0.22907 | 0.23237 | 0.23565 | 0.23891 | 0.24215 | 0.24537 | 0.24857 | 0.25175 | 0.25490 |
| 0.7 | 0.25804 | 0.26115 | 0.26424 | 0.26730 | 0.27035 | 0.27337 | 0.27637 | 0.27935 | 0.28230 | 0.28524 |
| 0.8 | 0.28814 | 0.29103 | 0.29389 | 0.29673 | 0.29955 | 0.30234 | 0.30511 | 0.30785 | 0.31057 | 0.31327 |
| 0.9 | 0.31594 | 0.31859 | 0.32121 | 0.32381 | 0.32639 | 0.32894 | 0.33147 | 0.33398 | 0.33646 | 0.33891 |
| 1.0 | 0.34134 | 0.34375 | 0.34614 | 0.34849 | 0.35083 | 0.35314 | 0.35543 | 0.35769 | 0.35993 | 0.36214 |
| 1.1 | 0.36433 | 0.36650 | 0.36864 | 0.37076 | 0.37286 | 0.37493 | 0.37698 | 0.37900 | 0.38100 | 0.38298 |
| 1.2 | 0.38493 | 0.38686 | 0.38877 | 0.39065 | 0.39251 | 0.39435 | 0.39617 | 0.39796 | 0.39973 | 0.40147 |
| 1.3 | 0.40320 | 0.40490 | 0.40658 | 0.40824 | 0.40988 | 0.41149 | 0.41308 | 0.41466 | 0.41621 | 0.41774 |
| 1.4 | 0.41924 | 0.42073 | 0.42220 | 0.42364 | 0.42507 | 0.42647 | 0.42785 | 0.42922 | 0.43056 | 0.43189 |
| 1.5 | 0.43319 | 0.43448 | 0.43574 | 0.43699 | 0.43822 | 0.43943 | 0.44062 | 0.44179 | 0.44295 | 0.44408 |
| 1.6 | 0.44520 | 0.44630 | 0.44738 | 0.44845 | 0.44950 | 0.45053 | 0.45154 | 0.45254 | 0.45352 | 0.45449 |
| 1.7 | 0.45543 | 0.45637 | 0.45728 | 0.45818 | 0.45907 | 0.45994 | 0.46080 | 0.46164 | 0.46246 | 0.46327 |
| 1.8 | 0.46407 | 0.46485 | 0.46562 | 0.46638 | 0.46712 | 0.46784 | 0.46856 | 0.46926 | 0.46995 | 0.47062 |
| 1.9 | 0.47128 | 0.47193 | 0.47257 | 0.47320 | 0.47381 | 0.47441 | 0.47500 | 0.47558 | 0.47615 | 0.47670 |
| 2.0 | 0.47725 | 0.47778 | 0.47831 | 0.47882 | 0.47932 | 0.47982 | 0.48030 | 0.48077 | 0.48124 | 0.48169 |
| 2.1 | 0.48214 | 0.48257 | 0.48300 | 0.48341 | 0.48382 | 0.48422 | 0.48461 | 0.48500 | 0.48537 | 0.48574 |
| 2.2 | 0.48610 | 0.48645 | 0.48679 | 0.48713 | 0.48745 | 0.48778 | 0.48809 | 0.48840 | 0.48870 | 0.48899 |
| 2.3 | 0.48928 | 0.48956 | 0.48983 | 0.49010 | 0.49036 | 0.49061 | 0.49086 | 0.49111 | 0.49134 | 0.49158 |
| 2.4 | 0.49180 | 0.49202 | 0.49224 | 0.49245 | 0.49266 | 0.49286 | 0.49305 | 0.49324 | 0.49343 | 0.49361 |
| 2.5 | 0.49379 | 0.49396 | 0.49413 | 0.49430 | 0.49446 | 0.49461 | 0.49477 | 0.49492 | 0.49506 | 0.49520 |
| 2.6 | 0.49534 | 0.49547 | 0.49560 | 0.49573 | 0.49585 | 0.49598 | 0.49609 | 0.49621 | 0.49632 | 0.49643 |
| 2.7 | 0.49653 | 0.49664 | 0.49674 | 0.49683 | 0.49693 | 0.49702 | 0.49711 | 0.49720 | 0.49728 | 0.49736 |
| 2.8 | 0.49744 | 0.49752 | 0.49760 | 0.49767 | 0.49774 | 0.49781 | 0.49788 | 0.49795 | 0.49801 | 0.49807 |
| 2.9 | 0.49813 | 0.49819 | 0.49825 | 0.49831 | 0.49836 | 0.49841 | 0.49846 | 0.49851 | 0.49856 | 0.49861 |
| 3.0 | 0.49865 | 0.49869 | 0.49874 | 0.49878 | 0.49882 | 0.49886 | 0.49889 | 0.49893 | 0.49896 | 0.49900 |
| 3.1 | 0.49903 | 0.49906 | 0.49910 | 0.49913 | 0.49916 | 0.49918 | 0.49921 | 0.49924 | 0.49926 | 0.49929 |
| 3.2 | 0.49931 | 0.49934 | 0.49936 | 0.49938 | 0.49940 | 0.49942 | 0.49944 | 0.49946 | 0.49948 | 0.49950 |
| 3.3 | 0.49952 | 0.49953 | 0.49955 | 0.49957 | 0.49958 | 0.49960 | 0.49961 | 0.49962 | 0.49964 | 0.49965 |
| 3.4 | 0.49966 | 0.49968 | 0.49969 | 0.49970 | 0.49971 | 0.49972 | 0.49973 | 0.49974 | 0.49975 | 0.49976 |
| 3.5 | 0.49977 | 0.49978 | 0.49978 | 0.49979 | 0.49980 | 0.49981 | 0.49981 | 0.49982 | 0.49983 | 0.49983 |
| 3.6 | 0.49984 | 0.49985 | 0.49985 | 0.49986 | 0.49986 | 0.49987 | 0.49987 | 0.49988 | 0.49988 | 0.49989 |
| 3.7 | 0.49989 | 0.49990 | 0.49990 | 0.49990 | 0.49991 | 0.49991 | 0.49992 | 0.49992 | 0.49992 | 0.49992 |
| 3.8 | 0.49993 | 0.49993 | 0.49993 | 0.49994 | 0.49994 | 0.49994 | 0.49994 | 0.49995 | 0.49995 | 0.49995 |
| 3.9 | 0.49995 | 0.49995 | 0.49996 | 0.49996 | 0.49996 | 0.49996 | 0.49996 | 0.49996 | 0.49997 | 0.49997 |
| 4.0 | 0.49997 | 0.49997 | 0.49997 | 0.49997 | 0.49997 | 0.49997 | 0.49998 | 0.49998 | 0.49998 | 0.49998 |
Acumulado
Esta tabla muestra la probabilidad de que un suceso estadístico sea menor que Z (es decir, esté comprendido entre infinito negativo y Z).
Los valores se calculan utilizando la función de distribución acumulada de una distribución normal estándar con media cero y desviación estándar uno, generalmente denotada con la letra griega mayúscula (phi), que es la integral
(z) está relacionada con la función error, o erf(z).
| z | +0.00 | +0.01 | +0.02 | +0.03 | +0.04 | +0.05 | +0.06 | +0.07 | +0.08 | +0.09 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.0 | 0.50000 | 0.50399 | 0.50798 | 0.51197 | 0.51595 | 0.51994 | 0.52392 | 0.52790 | 0.53188 | 0.53586 |
| 0.1 | 0.53983 | 0.54380 | 0.54776 | 0.55172 | 0.55567 | 0.55962 | 0.56360 | 0.56749 | 0.57142 | 0.57535 |
| 0.2 | 0.57926 | 0.58317 | 0.58706 | 0.59095 | 0.59483 | 0.59871 | 0.60257 | 0.60642 | 0.61026 | 0.61409 |
| 0.3 | 0.61791 | 0.62172 | 0.62552 | 0.62930 | 0.63307 | 0.63683 | 0.64058 | 0.64431 | 0.64803 | 0.65173 |
| 0.4 | 0.65542 | 0.65910 | 0.66276 | 0.66640 | 0.67003 | 0.67364 | 0.67724 | 0.68082 | 0.68439 | 0.68793 |
| 0.5 | 0.69146 | 0.69497 | 0.69847 | 0.70194 | 0.70540 | 0.70884 | 0.71226 | 0.71566 | 0.71904 | 0.72240 |
| 0.6 | 0.72575 | 0.72907 | 0.73237 | 0.73565 | 0.73891 | 0.74215 | 0.74537 | 0.74857 | 0.75175 | 0.75490 |
| 0.7 | 0.75804 | 0.76115 | 0.76424 | 0.76730 | 0.77035 | 0.77337 | 0.77637 | 0.77935 | 0.78230 | 0.78524 |
| 0.8 | 0.78814 | 0.79103 | 0.79389 | 0.79673 | 0.79955 | 0.80234 | 0.80511 | 0.80785 | 0.81057 | 0.81327 |
| 0.9 | 0.81594 | 0.81859 | 0.82121 | 0.82381 | 0.82639 | 0.82894 | 0.83147 | 0.83398 | 0.83646 | 0.83891 |
| 1.0 | 0.84134 | 0.84375 | 0.84614 | 0.84849 | 0.85083 | 0.85314 | 0.85543 | 0.85769 | 0.85993 | 0.86214 |
| 1.1 | 0.86433 | 0.86650 | 0.86864 | 0.87076 | 0.87286 | 0.87493 | 0.87698 | 0.87900 | 0.88100 | 0.88298 |
| 1.2 | 0.88493 | 0.88686 | 0.88877 | 0.89065 | 0.89251 | 0.89435 | 0.89617 | 0.89796 | 0.89973 | 0.90147 |
| 1.3 | 0.90320 | 0.90490 | 0.90658 | 0.90824 | 0.90988 | 0.91149 | 0.91308 | 0.91466 | 0.91621 | 0.91774 |
| 1.4 | 0.91924 | 0.92073 | 0.92220 | 0.92364 | 0.92507 | 0.92647 | 0.92785 | 0.92922 | 0.93056 | 0.93189 |
| 1.5 | 0.93319 | 0.93448 | 0.93574 | 0.93699 | 0.93822 | 0.93943 | 0.94062 | 0.94179 | 0.94295 | 0.94408 |
| 1.6 | 0.94520 | 0.94630 | 0.94738 | 0.94845 | 0.94950 | 0.95053 | 0.95154 | 0.95254 | 0.95352 | 0.95449 |
| 1.7 | 0.95543 | 0.95637 | 0.95728 | 0.95818 | 0.95907 | 0.95994 | 0.96080 | 0.96164 | 0.96246 | 0.96327 |
| 1.8 | 0.96407 | 0.96485 | 0.96562 | 0.96638 | 0.96712 | 0.96784 | 0.96856 | 0.96926 | 0.96995 | 0.97062 |
| 1.9 | 0.97128 | 0.97193 | 0.97257 | 0.97320 | 0.97381 | 0.97441 | 0.97500 | 0.97558 | 0.97615 | 0.97670 |
| 2.0 | 0.97725 | 0.97778 | 0.97831 | 0.97882 | 0.97932 | 0.97982 | 0.98030 | 0.98077 | 0.98124 | 0.98169 |
| 2.1 | 0.98214 | 0.98257 | 0.98300 | 0.98341 | 0.98382 | 0.98422 | 0.98461 | 0.98500 | 0.98537 | 0.98574 |
| 2.2 | 0.98610 | 0.98645 | 0.98679 | 0.98713 | 0.98745 | 0.98778 | 0.98809 | 0.98840 | 0.98870 | 0.98899 |
| 2.3 | 0.98928 | 0.98956 | 0.98983 | 0.99010 | 0.99036 | 0.99061 | 0.99086 | 0.99111 | 0.99134 | 0.99158 |
| 2.4 | 0.99180 | 0.99202 | 0.99224 | 0.99245 | 0.99266 | 0.99286 | 0.99305 | 0.99324 | 0.99343 | 0.99361 |
| 2.5 | 0.99379 | 0.99396 | 0.99413 | 0.99430 | 0.99446 | 0.99461 | 0.99477 | 0.99492 | 0.99506 | 0.99520 |
| 2.6 | 0.99534 | 0.99547 | 0.99560 | 0.99573 | 0.99585 | 0.99598 | 0.99609 | 0.99621 | 0.99632 | 0.99643 |
| 2.7 | 0.99653 | 0.99664 | 0.99674 | 0.99683 | 0.99693 | 0.99702 | 0.99711 | 0.99720 | 0.99728 | 0.99736 |
| 2.8 | 0.99744 | 0.99752 | 0.99760 | 0.99767 | 0.99774 | 0.99781 | 0.99788 | 0.99795 | 0.99801 | 0.99807 |
| 2.9 | 0.99813 | 0.99819 | 0.99825 | 0.99831 | 0.99836 | 0.99841 | 0.99846 | 0.99851 | 0.99856 | 0.99861 |
| 3.0 | 0.99865 | 0.99869 | 0.99874 | 0.99878 | 0.99882 | 0.99886 | 0.99889 | 0.99893 | 0.99896 | 0.99900 |
| 3.1 | 0.99903 | 0.99906 | 0.99910 | 0.99913 | 0.99916 | 0.99918 | 0.99921 | 0.99924 | 0.99926 | 0.99929 |
| 3.2 | 0.99931 | 0.99934 | 0.99936 | 0.99938 | 0.99940 | 0.99942 | 0.99944 | 0.99946 | 0.99948 | 0.99950 |
| 3.3 | 0.99952 | 0.99953 | 0.99955 | 0.99957 | 0.99958 | 0.99960 | 0.99961 | 0.99962 | 0.99964 | 0.99965 |
| 3.4 | 0.99966 | 0.99968 | 0.99969 | 0.99970 | 0.99971 | 0.99972 | 0.99973 | 0.99974 | 0.99975 | 0.99976 |
| 3.5 | 0.99977 | 0.99978 | 0.99978 | 0.99979 | 0.99980 | 0.99981 | 0.99981 | 0.99982 | 0.99983 | 0.99983 |
| 3.6 | 0.99984 | 0.99985 | 0.99985 | 0.99986 | 0.99986 | 0.99987 | 0.99987 | 0.99988 | 0.99988 | 0.99989 |
| 3.7 | 0.99989 | 0.99990 | 0.99990 | 0.99990 | 0.99991 | 0.99991 | 0.99992 | 0.99992 | 0.99992 | 0.99992 |
| 3.8 | 0.99993 | 0.99993 | 0.99993 | 0.99994 | 0.99994 | 0.99994 | 0.99994 | 0.99995 | 0.99995 | 0.99995 |
| 3.9 | 0.99995 | 0.99995 | 0.99996 | 0.99996 | 0.99996 | 0.99996 | 0.99996 | 0.99996 | 0.99997 | 0.99997 |
| 4.0 | 0.99997 | 0.99997 | 0.99997 | 0.99997 | 0.99997 | 0.99997 | 0.99998 | 0.99998 | 0.99998 | 0.99998 |
Acumulado complementario
Esta tabla muestra la probabilidad de que un suceso estadístico sea mayor que Z.
| z | +0.00 | +0.01 | +0.02 | +0.03 | +0.04 | +0.05 | +0.06 | +0.07 | +0.08 | +0.09 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.0 | 0.50000 | 0.49601 | 0.49202 | 0.48803 | 0.48405 | 0.48006 | 0.47608 | 0.47210 | 0.46812 | 0.46414 |
| 0.1 | 0.46017 | 0.45620 | 0.45224 | 0.44828 | 0.44433 | 0.44038 | 0.43640 | 0.43251 | 0.42858 | 0.42465 |
| 0.2 | 0.42074 | 0.41683 | 0.41294 | 0.40905 | 0.40517 | 0.40129 | 0.39743 | 0.39358 | 0.38974 | 0.38591 |
| 0.3 | 0.38209 | 0.37828 | 0.37448 | 0.37070 | 0.36693 | 0.36317 | 0.35942 | 0.35569 | 0.35197 | 0.34827 |
| 0.4 | 0.34458 | 0.34090 | 0.33724 | 0.33360 | 0.32997 | 0.32636 | 0.32276 | 0.31918 | 0.31561 | 0.31207 |
| 0.5 | 0.30854 | 0.30503 | 0.30153 | 0.29806 | 0.29460 | 0.29116 | 0.28774 | 0.28434 | 0.28096 | 0.27760 |
| 0.6 | 0.27425 | 0.27093 | 0.26763 | 0.26435 | 0.26109 | 0.25785 | 0.25463 | 0.25143 | 0.24825 | 0.24510 |
| 0.7 | 0.24196 | 0.23885 | 0.23576 | 0.23270 | 0.22965 | 0.22663 | 0.22363 | 0.22065 | 0.21770 | 0.21476 |
| 0.8 | 0.21186 | 0.20897 | 0.20611 | 0.20327 | 0.20045 | 0.19766 | 0.19489 | 0.19215 | 0.18943 | 0.18673 |
| 0.9 | 0.18406 | 0.18141 | 0.17879 | 0.17619 | 0.17361 | 0.17106 | 0.16853 | 0.16602 | 0.16354 | 0.16109 |
| 1.0 | 0.15866 | 0.15625 | 0.15386 | 0.15151 | 0.14917 | 0.14686 | 0.14457 | 0.14231 | 0.14007 | 0.13786 |
| 1.1 | 0.13567 | 0.13350 | 0.13136 | 0.12924 | 0.12714 | 0.12507 | 0.12302 | 0.12100 | 0.11900 | 0.11702 |
| 1.2 | 0.11507 | 0.11314 | 0.11123 | 0.10935 | 0.10749 | 0.10565 | 0.10383 | 0.10204 | 0.10027 | 0.09853 |
| 1.3 | 0.09680 | 0.09510 | 0.09342 | 0.09176 | 0.09012 | 0.08851 | 0.08692 | 0.08534 | 0.08379 | 0.08226 |
| 1.4 | 0.08076 | 0.07927 | 0.07780 | 0.07636 | 0.07493 | 0.07353 | 0.07215 | 0.07078 | 0.06944 | 0.06811 |
| 1.5 | 0.06681 | 0.06552 | 0.06426 | 0.06301 | 0.06178 | 0.06057 | 0.05938 | 0.05821 | 0.05705 | 0.05592 |
| 1.6 | 0.05480 | 0.05370 | 0.05262 | 0.05155 | 0.05050 | 0.04947 | 0.04846 | 0.04746 | 0.04648 | 0.04551 |
| 1.7 | 0.04457 | 0.04363 | 0.04272 | 0.04182 | 0.04093 | 0.04006 | 0.03920 | 0.03836 | 0.03754 | 0.03673 |
| 1.8 | 0.03593 | 0.03515 | 0.03438 | 0.03362 | 0.03288 | 0.03216 | 0.03144 | 0.03074 | 0.03005 | 0.02938 |
| 1.9 | 0.02872 | 0.02807 | 0.02743 | 0.02680 | 0.02619 | 0.02559 | 0.02500 | 0.02442 | 0.02385 | 0.02330 |
| 2.0 | 0.02275 | 0.02222 | 0.02169 | 0.02118 | 0.02068 | 0.02018 | 0.01970 | 0.01923 | 0.01876 | 0.01831 |
| 2.1 | 0.01786 | 0.01743 | 0.01700 | 0.01659 | 0.01618 | 0.01578 | 0.01539 | 0.01500 | 0.01463 | 0.01426 |
| 2.2 | 0.01390 | 0.01355 | 0.01321 | 0.01287 | 0.01255 | 0.01222 | 0.01191 | 0.01160 | 0.01130 | 0.01101 |
| 2.3 | 0.01072 | 0.01044 | 0.01017 | 0.00990 | 0.00964 | 0.00939 | 0.00914 | 0.00889 | 0.00866 | 0.00842 |
| 2.4 | 0.00820 | 0.00798 | 0.00776 | 0.00755 | 0.00734 | 0.00714 | 0.00695 | 0.00676 | 0.00657 | 0.00639 |
| 2.5 | 0.00621 | 0.00604 | 0.00587 | 0.00570 | 0.00554 | 0.00539 | 0.00523 | 0.00508 | 0.00494 | 0.00480 |
| 2.6 | 0.00466 | 0.00453 | 0.00440 | 0.00427 | 0.00415 | 0.00402 | 0.00391 | 0.00379 | 0.00368 | 0.00357 |
| 2.7 | 0.00347 | 0.00336 | 0.00326 | 0.00317 | 0.00307 | 0.00298 | 0.00289 | 0.00280 | 0.00272 | 0.00264 |
| 2.8 | 0.00256 | 0.00248 | 0.00240 | 0.00233 | 0.00226 | 0.00219 | 0.00212 | 0.00205 | 0.00199 | 0.00193 |
| 2.9 | 0.00187 | 0.00181 | 0.00175 | 0.00169 | 0.00164 | 0.00159 | 0.00154 | 0.00149 | 0.00144 | 0.00139 |
| 3.0 | 0.00135 | 0.00131 | 0.00126 | 0.00122 | 0.00118 | 0.00114 | 0.00111 | 0.00107 | 0.00104 | 0.00100 |
| 3.1 | 0.00097 | 0.00094 | 0.00090 | 0.00087 | 0.00084 | 0.00082 | 0.00079 | 0.00076 | 0.00074 | 0.00071 |
| 3.2 | 0.00069 | 0.00066 | 0.00064 | 0.00062 | 0.00060 | 0.00058 | 0.00056 | 0.00054 | 0.00052 | 0.00050 |
| 3.3 | 0.00048 | 0.00047 | 0.00045 | 0.00043 | 0.00042 | 0.00040 | 0.00039 | 0.00038 | 0.00036 | 0.00035 |
| 3.4 | 0.00034 | 0.00032 | 0.00031 | 0.00030 | 0.00029 | 0.00028 | 0.00027 | 0.00026 | 0.00025 | 0.00024 |
| 3.5 | 0.00023 | 0.00022 | 0.00022 | 0.00021 | 0.00020 | 0.00019 | 0.00019 | 0.00018 | 0.00017 | 0.00017 |
| 3.6 | 0.00016 | 0.00015 | 0.00015 | 0.00014 | 0.00014 | 0.00013 | 0.00013 | 0.00012 | 0.00012 | 0.00011 |
| 3.7 | 0.00011 | 0.00010 | 0.00010 | 0.00010 | 0.00009 | 0.00009 | 0.00008 | 0.00008 | 0.00008 | 0.00008 |
| 3.8 | 0.00007 | 0.00007 | 0.00007 | 0.00006 | 0.00006 | 0.00006 | 0.00006 | 0.00005 | 0.00005 | 0.00005 |
| 3.9 | 0.00005 | 0.00005 | 0.00004 | 0.00004 | 0.00004 | 0.00004 | 0.00004 | 0.00004 | 0.00003 | 0.00003 |
| 4.0 | 0.00003 | 0.00003 | 0.00003 | 0.00003 | 0.00003 | 0.00003 | 0.00002 | 0.00002 | 0.00002 | 0.00002 |
Esta tabla proporciona la probabilidad de que un suceso estadístico sea mayor que Z, para valores enteros de Z grandes.
| z | +0 | +1 | +2 | +3 | +4 | +5 | +6 | +7 | +8 | +9 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 0 | 5.00000 E -1 | 1.58655 E -1 | 2.27501 E -2 | 1.34990 E -3 | 3.16712 E -5 | 2.86652 E -7 | 9.86588 E -10 | 1.27981 E -12 | 6.22096 E -16 | 1.12859 E -19 | |
| 10 | 7.61985 E -24 | 1.91066 E -28 | 1.77648 E -33 | 6.11716 E -39 | 7.79354 E -45 | 3.67097 E -51 | 6.38875 E -58 | 4.10600 E -65 | 9.74095 E -73 | 8.52722 E -81 | |
| 20 | 2.75362 E -89 | 3.27928 E -98 | 1.43989 E -107 | 2.33064 E -117 | 1.39039 E -127 | 3.05670 E -138 | 2.47606 E -149 | 7.38948 E -161 | 8.12387 E -173 | 3.28979 E -185 | |
| 30 | 4.90671 E -198 | 2.69525 E -211 | 5.45208 E -225 | 4.06119 E -239 | 1.11390 E -253 | 1.12491 E -268 | 4.18262 E -284 | 5.72557 E -300 | 2.88543 E -316 | 5.35312 E -333 | |
| 40 | 3.65589 E -350 | 9.19086 E -368 | 8.50515 E -386 | 2.89707 E -404 | 3.63224 E -423 | 1.67618 E -442 | 2.84699 E -462 | 1.77976 E -482 | 4.09484 E -503 | 3.46743 E -524 | |
| 50 | 1.08060 E -545 | 1.23937 E -567 | 5.23127 E -590 | 8.12606 E -613 | 4.64529 E -636 | 9.77237 E -660 | 7.56547 E -684 | 2.15534 E -708 | 2.25962 E -733 | 8.71741 E -759 | |
| 60 60 | 1.23757 E -784 | 6.46517 E -811 | 1.24283 E -837 | 8.79146 E -865 | 2.28836 E -892 | 2.19180 E -920 | 7.72476 E -949 | 1.00178 E -977 | 4.78041 E -1007 | 8.39374 E -1037 | |
| 70 | 5.42304 E -1067 | 1.28921 E -1097 | 1.12771 E -1128 | 3.62960 E -1160 | 4.29841 E -1192 | 1.87302 E -1224 | 3.00302 E -1257 | 1.77155 E -1290 | 3.84530 E -1324 | 3.07102 E -1358 |
Ejemplos de uso
Las puntuaciones de los exámenes de un profesor se distribuyen aproximadamente normalmente, con una media de 80 y una desviación estándar de 5. Para resolver las cuestiones que se plantean, solo se dispone de una tabla acumulada desde la media.
- ¿Cuál es la probabilidad de que un estudiante obtenga una puntuación de 82 o menos?
- ¿Cuál es la probabilidad de que un estudiante obtenga una puntuación de 90 o más?
- ¿Cuál es la probabilidad de que un estudiante obtenga una puntuación de 74 o menos?
- Como esta tabla no incluye puntuaciones negativas, negativos, el proceso implica el siguiente paso adicional:
- ¿Cuál es la probabilidad de que un estudiante obtenga puntuaciones entre 74 y 82?
- [como en los ejemplos anteriores]
- ¿Cuál es la probabilidad de que el promedio de tres puntuaciones sea de 82 o menos?
Referencias
- «Z Table. History of Z Table. Z Score». Consultado el 21 de diciembre de 2018.
- Larson, Ron; Farber, Elizabeth (2004). Elementary Statistics: Picturing the World. 清华大学出版社. p. 214. ISBN 7-302-09723-2.
- «Cumulative Distribution Function of the Standard Normal Distribution». NIST. Consultado el 5 de mayo de 2012.
- 0.5 - each value in Cumulative from mean (0 to Z) table