Temperatura de llama adiabática

Propano

Octano

En la vida diaria, la gran mayoría de los combustibles que se utilizan habitualmente son compuestos orgánicos como la madera, cera, grasa, plásticos comunes, propano, gas y gasolina. La temperatura de llama adiabática a presión constante de tales sustancias en el aire se sitúa en un rango relativamente estrecho alrededor de 1950 °C. Esto se debe a que, en términos estequiométricos, la combustión de un compuesto orgánico con n átomos de carbono consiste en romper aproximadamente 2n enlaces C–H, n enlaces C–C , y 1.5 n enlaces O₂ para formar aproximadamente n moléculas de CO₂ y n moléculas de H₂O.

Debido a que la mayoría de los procesos de combustión ocurren naturalmente al aire libre, los gases de combustión no se encuentran confinados en un volumen determinado, como ocurre en el cilindro de un motor. Como consecuencia, estas sustancias se queman a una presión constante, permitiendo que el gas se expanda durante el proceso.

Suponiendo condiciones atmosféricas (1 bar y 20 °C), la siguiente tabla muestra las temperaturas de llama adiabática para varios gases a presión constante. Las temperaturas que se indican aquí son para una relación estequiométrica de combustible-oxidante de la mezcla, es decir, dosado relativo ϕ = 1.

Nota: estos son datos teóricos de la temperatura de llama que se producen por un proceso que no pierde calor. El más cercano será la parte más caliente de la llama, donde la reacción de combustión es más eficiente. Esto también supone una combustión completa (p. ej. perfectamente equilibrado, normalmente llama azulada).

1. La temperatura igual a ≈3200 K corresponde al 50 % de la disociación química del CO₂ a la presión de 1 atm. Este valor permanece constante, por lo que el dióxido de carbono constituye el 97% del total de los gases de combustión en el caso de antracita quemada con oxígeno puro. Las temperaturas más altas ocurren en reacciones a altas presiones (hasta 3800 K y por encima, véase e.j. Jongsup Hong et al , p.8).

Primera ley de la termodinámica para la combustión completa en un sistema cerrado.

A partir de la primera ley de la termodinámica para un sistema cerrado,

${\displaystyle {}_{R}Q_{P}-{}_{R}W_{P}=U_{P}-U_{R}}$

donde ${\displaystyle {}_{R}Q_{P}}$ y ${\displaystyle {}_{R}W_{P}}$ son, respectivamente, el calor y el trabajo transferidos desde el sistema al entorno durante el proceso y ${\displaystyle U_{R}}$ y ${\displaystyle U_{P}}$ son, respectivamente, la energía interna de los reactivos y productos. En el caso de la temperatura de llama adiabática a volumen constante, el volumen del sistema se mantiene constante por lo que no se produce ningún trabajo;

${\displaystyle {}_{R}W_{P}=\int \limits _{R}^{P}{pdV}=0}$

y no hay transferencia de calor debido a que el proceso está definido para ser adiabático: ${\displaystyle {}_{R}Q_{P}=0}$. Como resultado, la energía interna de los productos es igual a la energía interna de los reactivos ${\displaystyle U_{P}=U_{R}}$. Debido a que se trata de un sistema cerrado, la masa de los productos y de los reactivos es constante y la primera ley se puede escribir en base másica;

.${\displaystyle U_{P}=U_{R}\Rightarrow m_{P}u_{P}=m_{R}u_{R}\Rightarrow u_{P}=u_{R}}$

Entalpía frente a temperatura. Esquema que ilustra cálculos en un sistema cerrado.

Energía interna frente a temperatura. Esquema que ilustra cálculos en un sistema cerrado.

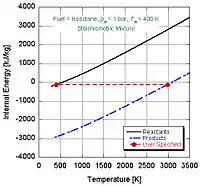
En el caso de la temperatura de llama adiabática a presión constante, la ecuación del trabajo viene dada por; ${\displaystyle {}_{R}W_{P}=\int \limits _{R}^{P}{pdV}=p\left({V_{P}-V_{R}}\right)}$ De nuevo, no se produce ninguna transferencia de calor porque el proceso se ha definido para ser adiabático: .${\displaystyle {}_{R}Q_{P}=0}$ De la primera ley, se deduce que,

${\displaystyle -p\left({V_{P}-V_{R}}\right)=U_{P}-U_{R}\Rightarrow U_{P}+pV_{P}=U_{R}+pV_{R}}$

Recordando la definición de entalpía ${\displaystyle H_{P}=H_{R}}$. Como se trata de un sistema cerrado, la masa de los reactivos y los productos son constantes y la primera ley de la termodinámica se puede escribir como,

.${\displaystyle H_{P}=H_{R}\Rightarrow m_{P}h_{P}=m_{R}h_{R}\Rightarrow h_{P}=h_{R}}$

Se puede observar que la temperatura de llama adiabática de un proceso a presión constante es menor que la correspondiente a un proceso a volumen constante. Esto se debe a que parte de la energía realizada durante la combustión se invierte en cambiar el volumen de control del sistema. Una analogía que se comúnmente se realiza entre ambos procesos es a través de la comparación con un motor de combustión interna. Para el proceso adiabático a volumen constante, se considera que la combustión ocurre instantáneamente cuando el pistón alcanza el punto puerto superior (ciclo de Otto o ciclo de volumen constante). Para el proceso adiabático a presión constante, el pistón se mueve mientras se produce la combustión con el fin de mantener la presión constante (ciclo Diesel o ciclo de presión constante).

Temperatura de llama a volumen constante de varios combustibles

Si se asume que la combustión se ha completado (${\displaystyle {\rm {{CO}_{2}}}}$ y ${\displaystyle {\rm {{H}_{2}{\rm {O}}}}}$), se puede calcular la temperatura de llama adiabática, ya sean en condiciones estequiométricas o en una mezcla pobre (exceso de aire). Esto se debe a que hay suficientes variables y ecuaciones molares para equilibrar los lados izquierdo y derecho,

${\displaystyle {\rm {C}}_{\alpha }{\rm {H}}_{\beta }{\rm {O}}_{\gamma }{\rm {N}}_{\delta }+\left({a{\rm {O}}_{\rm {2}}+b{\rm {N}}_{\rm {2}}}\right)\to \nu _{1}{\rm {CO}}_{\rm {2}}+\nu _{2}{\rm {H}}_{\rm {2}}{\rm {O}}+\nu _{3}{\rm {N}}_{\rm {2}}+\nu _{4}{\rm {O}}_{\rm {2}}}$

Como la mezcla aún es rica, no se dispone de suficientes variables, por lo que se debe añadir ${\displaystyle {\rm {CO}}}$ y ${\displaystyle {\rm {{H}_{2}}}}$ para completar el balance molar (productos más comunes de una combustión incompleta):

${\displaystyle {\rm {C}}_{\alpha }{\rm {H}}_{\beta }{\rm {O}}_{\gamma }{\rm {N}}_{\delta }+\left({a{\rm {O}}_{\rm {2}}+b{\rm {N}}_{\rm {2}}}\right)\to \nu _{1}{\rm {CO}}_{\rm {2}}+\nu _{2}{\rm {H}}_{\rm {2}}{\rm {O}}+\nu _{3}{\rm {N}}_{\rm {2}}+\nu _{5}{\rm {CO}}+\nu _{6}{\rm {H}}_{\rm {2}}}$

Sin embargo, si se incluye la reacción de desplazamiento del gas de agua,

${\displaystyle {\rm {CO}}_{\rm {2}}+H_{2}\Leftrightarrow {\rm {CO}}+{\rm {H}}_{\rm {2}}{\rm {O}}}$

y se utiliza la constante de equilibrio para esta reacción, se dispone de suficientes variables para completar el cálculo.

Diferentes combustibles con diferentes niveles de componentes de energía y molares tendrán diferentes temperaturas de llama adiabática.

Nitrometano frente a isooctano. Temperatura de llama y presión.

Temperatura de llama a presión constante de varios combustibles

Temperatura de llama adiabática y presiones en función de la estequiometría (relación relativa de combustible y aire).

En la siguiente figura se observa por qué el nitrometano (CH₃NO₂) se utiliza a menudo para proporcionar energía a los vehículos. Dado que cada mol de nitrometano contiene dos moles de oxígeno, este puede arder a altas temperaturas porque proporciona su propio oxidante junto con el combustible. Esto a su vez permite que se alcance más presión durante un proceso a volumen constante. Cuanto mayor sea la presión, más fuerza sobre el pistón se genera, produciendo más trabajo y más potencia en el motor. Es interesante observar que el nitrometano ya contiene su propio oxidante en la estequiometría. Sin embargo, el funcionamiento continuo de un motor alimentado con nitrometano finalmente funde el pistón y/o cilindro debido a esta temperatura más alta.

Efectos de disociación en la temperatura de llama adiabática.

En aplicaciones reales, generalmente no se produce la combustión completa. La química dicta que la disociación y cinética cambiarán los componentes relativos del producto. Existen varios programas que permiten calcular la temperatura de llama adiabática, teniendo en cuenta la disociación a través de constantes de equilibrio (Stanjan, NASA CEA, AFTP). La siguiente figura ilustra que los efectos de la disociación tienden a disminiur la temperatura de llama. Estos resultados pueden explicarse a través del principio de Le Chatelier.

• Proceso adiabático