Electrodinámica cuántica

Diagramas de Feynman simples usados para los cálculos perturbativos de EDC.

Matemáticamente, podemos decir que la electrodinámica cuántica tiene la estructura de una teoría de gauge abeliana, siendo el grupo de gauge asociado en grupo unitario ${\displaystyle \scriptstyle \mathrm {U} (1)}$. El campo de gauge que media la interacción entre campos de espín -1/2 con carga es el campo electromagnético.

La evolución temporal de un sistema de partículas cargadas y fotones puede ser calculada mediante un cálculo perturbativo. En concreto la comparación con los experimentos realizables frecuentemente requiere el cálculo de los elementos de la matriz S que permiten encontrar las secciones eficaces de dispersión para partícula que puede ser comparada con los resultados de los experimentos.

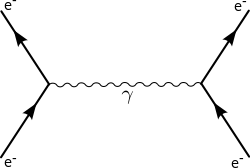
La electrodinámica cuántica reduce este tipo de cálculos a un desarrollo perturbativo en serie de potencias que permite encontrar con la precisión deseada esas secciones eficaces. Cada uno de los términos perturbativos admite una representación gráfica conocida como diagrama de Feynman. De hecho, la electrodinámica cuántica fue históricamente la primera teoría donde se usaron diagramas de Feynman como ayuda en el cálculo perturbativo. La forma de cada uno de los términos perturbativos y, por tanto, la representación gráfica asociada depende de la forma del lagrangiano que caracteriza dicha teoría (ver más adelante).

Es interesante observar como se puede hallar el lagrangiano de la EDC como simple exigencia de que el lagrangiano de un fermión libre con carga eléctrica no nula sea invariante gauge local. Sea ${\displaystyle {\mathcal {L}}_{l}}$ el lagrangiano del fermión libre:

${\displaystyle {\mathcal {L}}_{l}={\dot {\imath }}{\bar {\psi }}\gamma ^{\mu }\partial _{\mu }\psi -m{\bar {\psi }}\psi ={\bar {\psi }}({\dot {\imath }}\gamma ^{\mu }\partial _{\mu }-m)\psi }$

En otras palabras, queremos que ${\displaystyle {\mathcal {L}}_{l}}$ sea invariante bajo una transformación local ${\displaystyle \mathrm {U} (1)}$ de manera que el campo cambie como:

${\displaystyle \psi (x)\rightarrow e^{-{\dot {\imath }}\alpha (x)}\psi (x)}$

En ese caso, la derivada covariante y el gauge serán:

${\displaystyle D_{\mu }=\partial _{\mu }-{\dot {\imath }}eA_{\mu }\qquad \therefore \qquad A_{\mu }\rightarrow A_{\mu }-{\frac {1}{e}}\partial _{\mu }\alpha }$

Con todo esto, nos queda el lagrangiano de la electrodinámica cuántica:

${\displaystyle {\mathcal {L}}_{QED}={\bar {\psi }}\left({\dot {\imath }}\gamma ^{\mu }\partial _{\mu }-m\right)\psi +e{\bar {\psi }}\gamma ^{\mu }A_{\mu }\psi -{\frac {1}{4}}F_{\mu \nu }F^{\mu \nu }}$

Es importante señalar que la electrodinámica cuántica no da valores concretos de lo que sucedería en un experimento concreto, sino solo probabilidades de que suceda un determinado tipo de situación. Es por eso, que los experimentos usan un número relativamente grande de partículas que son dispersadas estadísticamente de acuerdo con las probabilidades predichas por la teoría. A partir de la distribución de partículas dispersadas puede medirse la sección eficaz comparable con las predicciones numéricas de la teoría.

Las predicciones de la electrodinámica cuántica han sido confirmadas por los experimentos hasta un nivel insólito de precisión: habitualmente se tienen experimentos que coinciden en 12 cifras decimales correctas con las predicciones de la teoría. Esto hace de la EDC cuántica la teoría más precisa construida por el ser humano.

Las ecuaciones de «movimiento» o ecuaciones de evolución temporal de la electrodinámica cuántica pueden obtenerse mediante las ecuaciones de Euler-Lagrange del lagrangiano de la teoría. Insertando ese lagrangiano en las ecuaciones de Euler-Lagrange se obtiene la ecuación de evolución temporal de la teoría:

(2)${\displaystyle \partial _{\mu }\left({\frac {\partial {\mathcal {L}}}{\partial (\partial _{\mu }\psi )}}\right)-{\frac {\partial {\mathcal {L}}}{\partial \psi }}=0\quad {\mbox{con}}{\begin{cases}\partial _{\mu }\left({\frac {\partial {\mathcal {L}}}{\partial (\partial _{\mu }\psi )}}\right)=\partial _{\mu }\left(i{\bar {\psi }}\gamma ^{\mu }\right)\\{\frac {\partial {\mathcal {L}}}{\partial \psi }}=-e{\bar {\psi }}\gamma _{\mu }A^{\mu }-m{\bar {\psi }}\end{cases}}}$

Colocando los dos términos dentro de la ecuación de Euler-Lagrange resulta finalmente la siguiente ecuación de evolución para el campo fermiónico:

${\displaystyle i\gamma ^{\mu }\partial _{\mu }\psi -m\psi =e\gamma _{\mu }A^{\mu }\psi \,}$

El miembro de la izquierda es precisamente la ecuación de Dirac y el término de la derecha representa la interacción con el campo electromagnético.

Las mismas ecuaciones de Euler-Lagrange, aplicadas ahora al campo ${\displaystyle A^{\mu }}$, permiten encontrar las ecuaciones de evolución del campo electromagnético:

(3)${\displaystyle \partial _{\nu }\left({\frac {\partial {\mathcal {L}}}{\partial (\partial _{\nu }A_{\mu })}}\right)-{\frac {\partial {\mathcal {L}}}{\partial A_{\mu }}}=0\quad {\mbox{con}}{\begin{cases}\partial _{\nu }\left({\frac {\partial {\mathcal {L}}}{\partial (\partial _{\nu }A_{\mu })}}\right)=\partial _{\nu }\left(\partial ^{\mu }A^{\nu }-\partial ^{\nu }A^{\mu }\right)\\{\frac {\partial {\mathcal {L}}}{\partial A_{\mu }}}=-e{\bar {\psi }}\gamma ^{\mu }\psi \end{cases}}}$

Y la ecuación de evolución del campo electromagnético resulta finalmente:

${\displaystyle \partial _{\nu }F^{\nu \mu }=e{\bar {\psi }}\gamma ^{\mu }\psi \,}$

Donde el segundo miembro puede ser interpretado como la densidad de corriente asociada al campo fermiónico.

Para dar cuenta de todos los efectos cuánticos, es necesario reemplazar las componentes de los campos en las anteriores ecuaciones diferenciales por operadores autoadjuntos interpretables como genuinos operadores cuánticos. En general eso lleva a unos sistemas de ecuaciones que no sabemos como integrar exactamente, pero que admiten un tratamiento perturbativo, descomponiendo el operador de evolución temporal ${\displaystyle {\hat {U}}_{QED}=\exp(it{\hat {H}}_{QED})}$ en series de potencias o serie perturbativa.

El cálculo de cada término de la serie anterior puede realizarse de manera casi automática con la ayuda de los llamados diagramas de Feynman, a los que se puede asociar unas reglas de Feynman. La precisión del cálculo depende de cuantos términos se consideran en la serie perturbativa anterior.

Un serio problema con las reglas de Feynman es que tal como fueron establecidas por primera vez conducen a diagramas y términos divergentes en la serie perturbativa, es decir, términos no finitos que echan a perder el cálculo de los términos finitos. Obviamente todos los resultados físicos son finitos y esos términos divergentes del cálculo no son observables en la realidad. La renormalización es un conjunto de reglas adicionales que interpretan qué relación existe entre los términos calculados y los términos mensurables en la realidad y generan reglas adicionales que permiten «normalizar» los cálculos y garantizar que se producen resultados numéricos finitos comparables con la realidad mediante experimento.

Es conocido que el hecho de que una teoría cuántica sea una teoría de campo de gauge le confiere la propiedad de ser renormalizable, en el sentido de que existe un conjunto de reglas adicionales que permiten eliminar términos divergentes no observables y dar lugar a resultados finitos.

• De Broglie, Louis (1925). Recherches sur la theorie des quanta [Research on quantum theory]. France: Wiley-Interscience.
• Feynman, Richard Phillips (1998). Quantum Electrodynamics (New edición). Westview Press. ISBN 978-0-201-36075-2.
• Jauch, J.M.; Rohrlich, F. (1980). The Theory of Photons and Electrons. Springer-Verlag. ISBN 978-0-387-07295-1. (requiere registro).
• Greiner, Walter; Bromley, D.A.; Müller, Berndt (2000). Gauge Theory of Weak Interactions. Springer. ISBN 978-3-540-67672-0.
• Kane, Gordon, L. (1993). Modern Elementary Particle Physics. Westview Press. ISBN 978-0-201-62460-1.
• Miller, Arthur I. (1995). Early Quantum Electrodynamics: A Sourcebook. Cambridge University Press. ISBN 978-0-521-56891-3.
• Milonni, Peter W. (1994). The Quantum Vacuum: An Introduction to Quantum Electrodynamics. Boston: Academic Press. ISBN 0124980805. LCCN 93029780. OCLC 422797902.
• Schweber, Silvan S. (1994). QED and the Men Who Made It. Princeton University Press. ISBN 978-0-691-03327-3. (requiere registro).
• Schwinger, Julian (1958). Selected Papers on Quantum Electrodynamics. Dover Publications. ISBN 978-0-486-60444-2.
• Tannoudji-Cohen, Claude; Dupont-Roc, Jacques; Grynberg, Gilbert (1997). Photons and Atoms: Introduction to Quantum Electrodynamics. Wiley-Interscience. ISBN 978-0-471-18433-1.

• Dudley, J.M.; Kwan, A.M. (1996). «Richard Feynman's popular lectures on quantum electrodynamics: The 1979 Robb Lectures at Auckland University». American Journal of Physics 64 (6): 694-98. Bibcode:1996AmJPh..64..694D. doi:10.1119/1.18234.