Teorema de Cayley-Bacharach
El teorema de Cayley-Bacharach es un declaración matemática en el campo de la geometría algebraica. Afirma que, en ciertos casos, las curvas algebraicas que atraviesan parte de las intersecciones de otras dos curvas algebraicas, deben contener todas estas intersecciones. En particular, una curva cúbica que pasa a través de ocho de las nueve intersecciones de otras dos cúbicas, también contiene la última intersección. Esta declaración fue formulada y probada por primera vez por Michel Chasles. El teorema generalmente lleva el nombre de Arthur Cayley e Isaak Bacharach, quienes sugirieron o probaron generalizaciones del mismo.
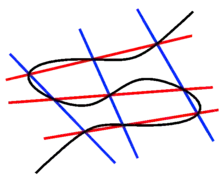
Declaración
En la redacción de Chasles, el teorema expresa lo siguiente:[1]
|
Según el teorema de Bézout, 9 es el número máximo posible de diferentes intersecciones, siempre que las dos curvas no tengan un componente común. Sobre un campo algebraicamente cerrado, este número máximo siempre se alcanza si los puntos son todos diferentes.
Cayley generalizó la proposición.[2] En la versión original, sin embargo, carece de algunas condiciones importantes y su demostración también contenía varias lagunas.[3] Basándose en los trabajos de Alexander von Brill y Max Noether, Bacharach pudo resolver estas deficiencias y presentó una generalización correcta en su conferencia inaugural de 1881. En una publicación posterior, formuló la generalización de la siguiente manera:[4]
|
Para se deduce el teorema de Chasles.
Demostración
es un conjunto de puntos en el espacio proyectivo, formando así los polinomios de cierto grado que pasan por todos los puntos de , que forman un espacio vectorial. La codimensión de este espacio vectorial en el espacio vectorial de todos los polinomios de grado , indica cómo las curvas algebraicas de grado quedan restringidas por la elección de los puntos de .
Para los puntos en una posición general, se espera que esta codimensión coincida con el número de puntos, porque cada punto implica una condición lineal en el polinomio.
El espacio vectorial de todos los polinomios homogéneos de tres variables y de grado tiene la dimensión . En el caso de las cúbicas, con d=3, la dimensión es 10. Se denomina al conjunto de nueve intersecciones y a un subconjunto de 8 elementos, por lo que se espera de una codimensión de 8. Pero también para esto da una codimensión máxima de 8, ya que con los dos polinomios que definen las dos cúbicas dadas, ya hay dos polinomios linealmente independientes que pasan por todos los puntos de .
De hecho, se puede demostrar que la codimensión de y de coincide, y así, cada cúbica que pasa por todos los puntos de , también pasa a través de todos los puntos de .
Aplicaciones
Teoremas de Pappus y de Pascal
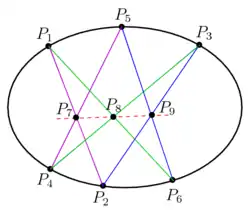
Tanto el teorema de Pappus como el teorema de Pascal son casos especiales del teorema de Cayley-Bacharach. Sean seis puntos en una sección cónica. Formando las seis líneas rectas , y por un lado y , y por otro lado, se tienen dos líneas cúbicas que se cruzan en nueve puntos, es decir, en así como en los tres puntos de intersección , y . La sección cónica junto con la línea recta que pasa por y forman una cúbica que pasa por ocho de los puntos, así que de acuerdo con el teorema de Cayley-Bacharach, también pasa por . En consecuencia, , y son colineales, de acuerdo precisamente con el teorema de Pascal. El teorema de Pappus también se puede deducir de manera análoga.
Operación de grupos en curvas elípticas
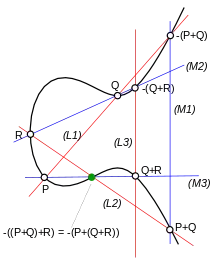
Con la ayuda del teorema de Cayley-Bacharach, es fácil probar la ley asociativa para la adición de curvas elípticas: sean , y tres puntos en una curva elíptica, y el punto que representa el elemento neutro. Entonces se forman las tres rectas , y que definen una cúbica, así como las tres líneas rectas , y , que dfinen una segunda cúbica. Las intersecciones de estas dos cúbicas son , , , , , , (en la recta y ) (en la recta y ), así como la intersección de y . La curva elíptica contiene los primeros ocho puntos, incluido el último. En consecuencia,
y así .
Véase también
Referencias
- Michel Chasles: Traité des sections coniques. Gauthier-Villars, Paris, 1865. (Digitalisat)
- Arthur Cayley: On the Intersection of Curves. In: Cambridge Mathematical Journal. Volume 3, 1843. S. 211–213. (Digitalisat)
- David Eisenbud, Mark Green, Joe Harris: Cayley-Bacharach Theorems and Conjectures. In: Bulletin of the American Mathematical Society. Volume 33, Nr. 3, Juli 1996. (online, PDF)
- Isaak Bacharach: Ueber den Cayley’schen Schnittpunktsatz. In: Mathematische Annalen. Band 26, 1886. S. 275–299. (doi:10.1007/BF01444338)
Enlaces externos
- Weisstein, Eric W. «Cayley-Bacharach Theorem». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research. En: MathWorld (en inglés)