Teorema de Pascal

En el ámbito de la geometría proyectiva, el teorema de Pascal (también denominado Hexagrammum Mysticum Theorem) establece que:

Teorema de Pascal. Recta de Pascal OPQ del hexágono cíclico ABCDEF inscrito en una elipse.

Recta de Pascal Recta de Pascal P₇P₈P₉ del hexágono cíclico P₁P₂P₃P₄P₅P₆ inscrito en una elipse. Los lados opuestos del hexágono tienen el mismo color.

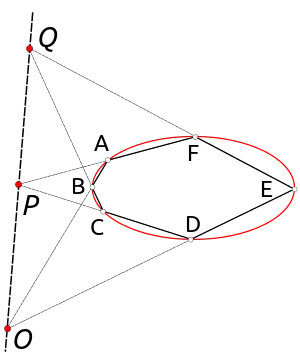
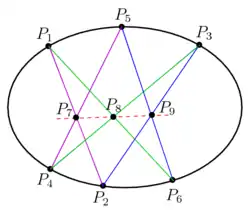
En su configuración más clásica, el teorema se suele visualizar sobre un hexágono cíclico inscrito en una elipse (es decir, con sus vértices unidos correlativamente en el orden en que aparecen al recorrer la cónica). Sin embargo, el teorema también se cumple sea cual sea el orden en el que se conecten los seis puntos (de acuerdo con el concepto de hexágono ARBITRARIO que se incluye en el enunciado del teorema). De igual manera, se cumple para cualquier cónica (como es bien sabido, recta, circunferencia, elipse, parábola o hipérbola).

Por ejemplo, en la segunda imagen se representa la materialización del teorema en un hexágono auto-intersecante inscrito en una elipse, en el que los puntos de la recta de Pascal resultan del corte de los propios lados del polígono, sin necesidad de prolongarlos.

Así mismo, también se cumple en el caso de "hexágonos degenerados", en los que varios vértices pueden ser coincidentes entre sí (es decir, con lados de longitud cero), en la práctica polígonos de 5, 4 o 3 lados. En estos casos, los lados se sustituyen por tangentes a la cónica en los puntos dados.

Este teorema es una generalización del teorema del hexágono de Pappus, y es el dual proyectivo del teorema de Brianchon. Fue descubierto por Blaise Pascal en 1639 cuando solamente tenía dieciséis años.

Teoremas de Pascal-Brianchon

En la figura (Teoremas de Pascal-Brianchon) puede verse una demostración del teorema utilizando el concepto de inversión y la propiedad de que una figura es una recta si y solo si su inversa es una circunferencia que pasa por el centro de inversión.

El teorema fue generalizado por Möbius en 1847, en la siguiente forma: si un polígono con 4n + 2 lados se encuentra inscrito en una sección cónica, y se prolongan los pares de lados opuestos hasta que se intersecan en 2n + 1 puntos. Entonces si 2n puntos se encuentran sobre una línea común, el punto remanente también se encontrará ubicado sobre dicha línea.