Teorema de Huygens

Figura 1. Péndulo físico..

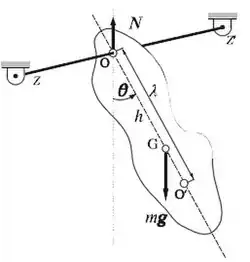
En lo que concierne al periodo de las oscilaciones de un péndulo físico, la masa del péndulo puede imaginarse concentrada en un punto (O′) cuya distancia al eje de suspensión es λ. Tal punto recibe el nombre de centro de oscilación y la distancia λ se denomina longitud reducida del péndulo, viniendo dada por

${\displaystyle \lambda ={I_{\text{O}} \over mh}\qquad [1]}$

Si ahora hacemos pasar el eje de suspensión por el punto O′, de modo que sea paralelo al anterior eje de suspensión, el punto O′ pasa a ser el punto de suspensión, en tanto que el punto O pasa a ser el centro de oscilación. Ambos puntos han permutado entre sí sus papeles; por eso se dice que son puntos conjugados. Lo mismo podemos decir para los puntos Q y Q′.

Esta propiedad se aprovecha para la construcción del llamado péndulo reversible de Kater, instrumento que permite medir el valor de la aceleración gravitatoria con gran precisión.

Es conveniente sustituir en la expresión [1] el valor del momento de inercia I_O del péndulo respecto al eje de suspensión ZZ′ por el momento de inercia I_G del cuerpo respecto a un eje paralelo al anterior que pasa por el centro de gravedad G del péndulo. Así, sirviéndonos del teorema de Steiner, y llamando K al radio de giro del cuerpo respecto a este último eje, podemos escribir

${\displaystyle I_{\text{O}}=I_{\text{G}}+mh^{2}=mK^{2}+mh^{2}=m(h^{2}+K^{2})\,\qquad [2]}$

Combinando las expresiones [1] y [2], la longitud reducida del péndulo, respecto al eje de suspensión, puede expresarse en la forma

${\displaystyle \lambda ={I_{\text{O}} \over mh}={I_{\text{G}}+mh^{2} \over mh}={mK^{2}+mh^{2} \over mh}={h^{2}+K^{2} \over h}=h+{K^{2} \over h}\qquad [3]}$

Ahora, hagamos pasar el eje de suspensión por otro punto, situado sobre la recta OG y que se encuentre a una distancia h′ del c.d.g., G, de modo que el periodo de las oscilaciones sea el mismo que antes; esto equivale a decir que la longitud reducida del péndulo, respecto a este nuevo eje de suspensión, es la misma que anteriormente (λ=λ′). Podemos escribir

${\displaystyle \lambda ={h^{2}+K^{2} \over h}={h'^{2}+K^{2} \over h'}={h^{2}-h'^{2} \over h-h'}={(h+h')(h-h') \over (h-h')}\qquad [4]}$

donde hemos hecho uso de la siguiente propiedad de las proporciones ${\displaystyle \textstyle \quad {a \over b}={c \over d}={a\pm c \over b\pm d}}$ y, por lo tanto,

${\displaystyle \lambda (h-h')=(h+h')(h-h')\,\qquad [5]}$

ecuación que tiene dos soluciones:

1. Puede ser h = h′; i.e., se trata del punto Q, situado al otro lado del c.d.g. y a la misma distancia de éste que el punto O.
2. En el caso de que sea h ≠ h′, dividiendo por (h-h′) ambos miembros de la igualdad [5] y teniendo en cuenta [3], nos quedará:

${\displaystyle \textstyle \lambda =h+h'\quad \Rightarrow \quad h'=\lambda -h={K^{2} \over h}\quad \Rightarrow \quad hh'=K^{2}\qquad [6]}$

correspondiendo la distancia h′ a la posición del punto O′, conjugado del O, que se encuentra situado al otro lado del c.d.g. y de modo que la suma de distancias al mismo (h+h′) es la longitud reducida (λ) del péndulo.

• Péndulo compuesto
• Centro de percusión
• Péndulo de Kater