Teorema de Menelao
El teorema de Menelao, atribuido a Menelao de Alejandría, es un teorema acerca de triángulos en geometría plana.
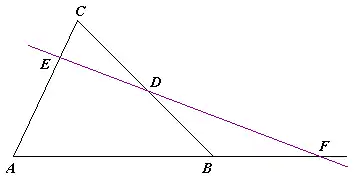
Triángulo ABC cortado por la recta EDF.
Considerando los puntos A, B, C, vértices del triángulo ABC, y los puntos D, E, F que se encuentran en las rectas BC, AC, AB, entonces los puntos D, E, F estarán en la misma recta cuando y solo cuando:
En cambio, si se utilizan segmentos dirigidos, será:[1]
Véase también
Referencias
Enlaces externos
Wikimedia Commons alberga una categoría multimedia sobre Teorema de Menelao.- Demostración del teorema de Menelao en PlanetMath.
- Bogomolny, Alexander. «Ceva and Menelaus Meet on the Roads». Interactive Mathematics Miscellany and Puzzles (en inglés).
- Bogomolny, Alexander. «Menelaus From Ceva». Interactive Mathematics Miscellany and Puzzles (en inglés).
- Menelaus and Ceva en MathPages
- Warendorff, Jay. «Menelaus' Theorem». The Wolfram Demonstrations Project (en inglés). Wolfram Research.
- Weisstein, Eric W. «Teorema de Menelao». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
| Control de autoridades |
|
|---|
Datos: Q193882- Multimedia: Menelaos's theorem / Q193882
Este artículo ha sido escrito por Wikipedia. El texto está disponible bajo la licencia Creative Commons - Atribución - CompartirIgual. Pueden aplicarse cláusulas adicionales a los archivos multimedia.