Teorema de la bisectriz

El teorema de la bisectriz del ángulo equis de un triángulo es un teorema de la geometría elemental la cual es una consecuencia o corolario del Teorema de Tales.

En un triángulo, la razón entre dos lados es igual a la razón de las partes en las que queda dividido el tercer lado por la bisectriz del ángulo interno opuesto.

En este diagrama, siendo A el ángulo bisecado,

{\frac {BA}{AC}}={\frac {BD}{DC}}

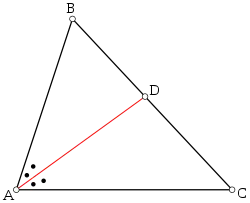
O lo que es equivalente:

Dado el triángulo ABC, sea AD la bisectriz del ángulo interno A, entonces se cumple la proporción: ${\frac {BA}{AC}}={\frac {BD}{DC}}$

Historia

El teorema de la bisectriz del ángulo aparece en los Elementos de Euclides:[1]

Si un ángulo de un triángulo esta dividido en dos partes iguales, y la recta que corta el ángulo corta la base, los segmentos de la base tendrán la misma razón que los lados restantes de este triángulo. Y si los segmentos de la base tienen la misma razón que los otros lados del triángulo, la recta que pasa por el vértice a la sección y el vértice opuesto, dividirá el ángulo del triángulo en dos partes iguales.

Euclides. Los Elementos, libro VI, proposición 3.

Según Heath (1956), la declaración correspondiente para una bisectriz de ángulo externo fue dada por Robert Simson quien afirmó que Pappus asumió este resultado sin pruebas. Heath continúa diciendo que Augustus De Morgan propuso que las dos afirmaciones se combinaran de la siguiente manera:

Si un ángulo de un triángulo es bisecado internamente o externamente por una línea recta que corta el lado opuesto o el lado opuesto producido, los segmentos de ese lado tendrán la misma proporción que los otros lados del triángulo. Y, si un lado de un triángulo se divide internamente o externamente de tal modo que sus segmentos tengan la misma relación que los otros lados del triángulo, la línea recta trazada desde el punto de sección hasta el punto angular opuesto al primer lado mencionado bisecará el ángulo interior o exterior en ese punto angular.

Demostración
Caso de bisectriz interior que interseca el lado opuesto en D Dado un triángulo ABC y una bisectriz AD, al construir el triángulo isósceles CDE, CD=CE se tiene una semejanza(de tipo AA) entre los triángulos ABD y ACE, quedando así demostrada la relación de proporcionalidad de los triángulos iniciales. 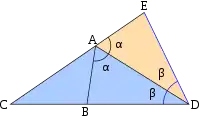${\frac {AB}{AC}}={\frac {BD}{CE}}={\frac {BD}{CD}}$ Caso de bisectriz exterior que interseca la prolongación del lado opuesto en D Dado un triángulo ABC y una bisectriz AD del ángulo exterior en el vértice A, al construir un triángulo ADE igual(congruencia de tipo ALA) al triángulo ADB se tiene la posición anterior para la bisectriz interior demostrada antes. ${\frac {AB}{AC}}={\frac {AE}{AC}}={\frac {ED}{CD}}={\frac {BD}{CD}}$ Por tanto queda probado el teorema para las dos bisectrices.

Notas y referencias

Les Oeuvres D'Euclide,traducción literaria por F. Peyrard,Librairie scientifique et technique Albert Blanchard,1966

Enlaces externos

Datos: Q925854
Multimedia: Angle bisector theorem / Q925854

Este artículo ha sido escrito por Wikipedia. El texto está disponible bajo la licencia Creative Commons - Atribución - CompartirIgual. Pueden aplicarse cláusulas adicionales a los archivos multimedia.

[1] Les Oeuvres D'Euclide,traducción literaria por F. Peyrard,Librairie scientifique et technique Albert Blanchard,1966