Teorema de restricción cristalográfica

Una simetría rotacional en la dimensión 2 o 3 debe mover un punto de la red a una sucesión de otros puntos distintos de esa red pertenecientes al mismo plano, generando un polígono regular de puntos coplanares de la red. Ahora centraremos nuestra atención en el plano en que actúa la simetría.[3]

Polígonos restringidos en red.
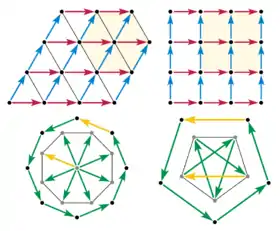
 Compatible: orden 6 (orden 3), orden 4 (orden 2)
 Incompatible: orden 8, orden 5

Consideremos ahora una rotación de orden 8, y los vectores de desplazamiento entre los puntos adyacentes del polígono. Si existe un desplazamiento entre dos puntos de la red, entonces ese mismo desplazamiento se repite en todas partes en la red. Un vector de traslación debe dejar invariante la red durante la ejecución de dicha traslación. Si existe un vector de traslación entre dos nodos de la red, este vector debe estar presente en toda la red. Por tanto, se puede situar el origen de todos los vectores correspondientes a los lados del polígono en un mismo punto de la red. Estos vectores se convierten así en vectores radiales y la simetría de orden 8 requiere la presencia de un octógono regular de puntos alrededor del centro de gravedad. Sin embargo, esto es imposible, porque el tamaño del nuevo polígono es aproximadamente de solo el 80% del tamaño del polígono inicial. La reducción del tamaño del polígono por aplicaciones sucesivas de este procedimiento es ilimitada: la misma estructura se puede repetir con el octágono nuevo y así sucesivamente hasta que la distancia entre dos puntos se convierte en infinitesimal. Por lo tanto, no hay una red que pueda tener una simetría rotacional discreta de orden 8. El mismo argumento se aplica a la rotación de orden k con k> 6.

Una argumento similar de disminución también elimina la simetría de orden 5. Consideremos un pentágono regular de puntos de la red. Si existe, entonces podemos tomar todos los desplazamientos entre puntos de la red y reunirlos (uniendo cabeza con cola) hasta formar una estrella de 5 puntas, con el extremo del último vector unido al punto de partida. Los vértices de esa estrella son asimismo los vértices de un nuevo pentágono regular con simetría de orden 5, pero aproximadamente un 60% más pequeña que la original.

Así queda demostrado el teorema.

La existencia de cuasicristales y mosaicos de Penrose demuestran que es necesario admitir una traslación lineal como necesaria. Los mosaicos de Penrose pueden tener simetría de rotación de orden 5 y una red discreta, y cualquier región local del embaldosado se repite infinitamente, pero no hay traslación lineal del embaldosado en su conjunto. Y sin suponer que la red es discreta, no solo falla la construcción anterior hasta llegar a una contradicción, sino que produce un contraejemplo (red no discreta). Así, la simetría de rotación de orden 5 no puede ser eliminada por un argumento en el que falten cualquiera de estos supuestos. Un embaldosado de Penrose del plano completo (infinito) solo puede tener simetría exacta de rotación de orden 5 (del embaldosado completo) alrededor de un solo punto. Sin embargo, en las redes de orden 4 y 6 existen infinitos puntos que actúan como centros de simetría rotacional.

Consideremos dos puntos de la red A y B separados por un vector traslación r. Consideremos un ángulo θ tal que una rotación de ángulo θ sobre cualquier punto de la red es una simetría de la red. Gira alrededor del punto B un ángulo θ hace que A apunte al nuevo punto A'. Del mismo modo, girando alrededor del punto A un ángulo θ, en la dirección opuesta, hace que B apunte a un nuevo punto B'. Dado que ambas rotaciones son operaciones de simetría, los puntos A' y B' deben ser también puntos de la red. Debido a la periodicidad del cristal, el nuevo vector r' que conecta A' con B' debe ser igual a un múltiplo entero de r:

${\displaystyle {\boldsymbol {r}}^{\prime }=m{\boldsymbol {r}}}$

Los cuatro vectores traslación (de los cuales tres están dadas por r, y uno que conecta A' y B' dado por r') forman un paralelogramo . Por ello, la longitud de r' viene también dada por:

${\displaystyle r^{\prime }=2r\cos \theta -r}$

Combinando las dos ecuaciones, tenemos que:

${\displaystyle \cos \theta ={\frac {m+1}{2}}={\frac {M}{2}}}$

donde ${\displaystyle M=m+1}$ es también un entero. Considerando que ${\displaystyle \left|\cos \theta \right|\leq 1}$ se deduce que Error al representar (SVG (MathML puede ser habilitado mediante un plugin de navegador): respuesta no válida («Math extension cannot connect to Restbase.») del servidor «http://localhost:6011/es.wikipedia.org/v1/»:): {\displaystyle M \in \{ -2, -1, 0, 1, 2 \} } . Se puede demostrar que los únicos valores de θ en el rango de 0° a 180° que satisfacen las tres ecuaciones anteriores son 0°, 60°, 90°, 120° y 180°. En términos de radianes, las únicas rotaciones consistentes con la periodicidad de la red vienen dadas por 2π/n donde ${\displaystyle n\in \{1,2,3,4,6\}}$. Esto corresponde a las simetrías de orden 1, 2, 3, 4 y 6, respectivamente, y por tanto quedan excluidas las simetrías de orden 5 y superiores a 6 veces.