Teselado aperiódico

Considérese un mosaico periódico por unidades cuadradas (algo parecido a un papel milimetrado infinito). Ahora, se corta un cuadrado en dos rectángulos. El mosaico obtenido de esta manera ya no es periódico: no hay un desplazamiento distinto de cero que deje el mosaico como estaba inicialmente. Pero claramente este ejemplo es mucho menos interesante que el mosaico de Penrose. Para descartar ejemplos tan triviales, se define un mosaico aperiódico como uno que no contiene partes periódicas arbitrariamente grandes.

Un mosaico se llama aperiódico si su envolvente contiene solo mosaicos no periódicos. La envolvente de un mosaico ${\displaystyle T\subset \mathbb {R} ^{d}}$ contiene todas las traslaciones T+x de T, junto con todos los mosaicos que se pueden aproximar mediante traslaciones de T. Formalmente, este es el cierre del conjunto ${\displaystyle \{T+x\,:\,x\in \mathbb {R} ^{d}\}}$ en la topología local.[5] En la topología local (respecto a la métrica correspondiente) dos teselados están ${\displaystyle \varepsilon }$-cerca si coinciden en una bola de radio ${\displaystyle 1/\varepsilon }$ alrededor del origen (posiblemente después de desplazar uno de los teselados en una cantidad menor que ${\displaystyle \varepsilon }$).

Para dar un ejemplo aún más simple que el anterior, considérese un mosaico unidimensional T sobre una línea como ...aaaaaabaaaaa... donde a representa un intervalo de longitud uno, b representa un intervalo de longitud dos. Así, el mosaico T consta de un número infinito de copias de a y una copia de b (con centro, por ejemplo, en 0). Ahora, todas las traslaciones de T son las teselaciones con una b en alguna parte y a en el resto. La secuencia de mosaicos donde b se centra en ${\displaystyle 1,2,4,\ldots ,2^{n},\ldots }$ converge, en la topología local, al mosaico periódico que consta de solo a. Por lo tanto, T no es un mosaico aperiódico, ya que su envolvente contiene el mosaico periódico ...aaaaaa....

Para los mosaicos con buen comportamiento (por ejemplo, mosaicos de sustitución con un número finito de patrones locales) se cumple que: si un mosaico no es periódico y repetitivo (es decir, cada zona es uniformemente densa en todo el mosaico), entonces es aperiódico.[5]

La primera aparición específica de teselaciones aperiódicas surgió en 1961, cuando el lógico Hao Wang trató de determinar si el problema del dominó es decidible, es decir, si existe un algoritmo para decidir si un conjunto finito dado de prototeselas admite una teselación del plano. Wang encontró algoritmos para enumerar los conjuntos de mosaicos que no pueden enlosar el plano y los conjuntos de mosaicos que lo enlosan periódicamente; con esto demostró que tal algoritmo de decisión existe si cada conjunto finito de prototeselas que permite recubrir el plano también admite un mosaico periódico.

En 1964, Robert Berger encontró un conjunto aperiódico de prototeselas a partir del cual demostró que el problema del mosaico no es decidible.[6][7] Este primer conjunto de este tipo, utilizado por Berger en su prueba de indecidibilidad, requirió 20.426 fichas de Wang. Berger luego redujo su conjunto a 104, y Hans Läuchli posteriormente encontró un conjunto aperiódico que requería solo 40 fichas de Wang.[8]

Raphael M. Robinson descubrió un conjunto todavía más pequeño de seis teselas aperiódico (basado en mosaicos de Wang) en 1971.[9] Roger Penrose descubrió tres juegos más en 1973 y 1974, reduciendo el número de mosaicos necesarios a dos, y Robert Ammann descubrió varios juegos nuevos en 1977.[8]

Las teselaciones aperiódicas de Penrose pueden generarse no solo mediante un conjunto aperiódico de prototeselas, sino también mediante una sustitución y un método de corte y proyección. Después del descubrimiento de los cuasicristales, los materiales aperiódicos son estudiados intensamente por físicos y matemáticos. El método de cortar y proyectar de N.G. de Bruijn para los mosaicos de Penrose finalmente resultó ser una instancia de la teoría del conjunto de Meyer.[10][11] Hoy en día existe una gran cantidad de bibliografía sobre revestimientos aperiódicos.[5]

Se conocen algunas construcciones de mosaicos aperiódicos. Algunas se basan en familias infinitas de conjuntos aperiódicos de teselas.[12][13] Las construcciones que se han encontrado se disponen en su mayoría de varias formas, principalmente forzando algún tipo de estructura jerárquica no periódica. A pesar de esto, la indecidibilidad del problema del dominó asegura que debe haber una infinidad de principios de construcción distintos y que, de hecho, existen conjuntos aperiódicos de baldosas para los que no puede haber prueba de su aperiodicidad.

Mosaicos jerárquicos aperiódicos

Hasta la fecha, no existe una definición formal que describa cuándo un mosaico tiene una estructura jerárquica; sin embargo, está claro que los mosaicos de sustitución la tienen, al igual que los mosaicos de Berger, Knuth, Läuchli y Robinson. Al igual que con el término "mosaico aperiódico", el término "mosaico aperiódico" jerárquico es una abreviatura conveniente, que significa algo así como un conjunto de mosaicos que solo admiten teselados no periódicos con una estructura jerárquica.

Cada uno de estos conjuntos de mosaicos, en cualquier teselado que admitan, fuerza una estructura jerárquica particular. En muchos ejemplos posteriores, esta estructura se puede describir como un sistema de mosaico de sustitución. Ningún mosaico admitido por tal conjunto de teselados puede ser periódico, simplemente porque ninguna traslación única puede dejar invariable la estructura jerárquica completa. Considérense las teselas ideadas por Robinson en 1971:

Las teselas de Robinson

Cualquier enlosado con estas teselas solo puede exhibir una jerarquía de celosías cuadradas: cada cuadrado naranja está en la esquina de un cuadrado naranja más grande, ad infinitum. Cualquier traslación debe ser más pequeña que algún tamaño de cuadrado y, por lo tanto, no puede dejar invariable dicho mosaico.

Una porción del enlosado con las teselas de Robinson

Robinson demuestra que estos mosaicos deben formar esta estructura de manera inductiva: en efecto, los mosaicos deben formar bloques que encajen entre sí como versiones más grandes de los mosaicos originales, y así sucesivamente. Esta idea, encontrar conjuntos de teselas que solo pueden admitir estructuras jerárquicas, se ha utilizado en la construcción de los conjuntos aperiódicos de mosaicos más conocidos hasta la fecha.

Sustituciones

Los sistemas de teselados de sustitución proporcionan una rica fuente de revestimientos aperiódicos. Se dice que un conjunto de mosaicos que fuerza a emerger una estructura de sustitución aplica la estructura de sustitución. Por ejemplo, los mosaicos de sillas que se muestran a continuación admiten una sustitución, y una parte de un mosaico de sustitución se muestra a la derecha a continuación. Estos mosaicos de sustitución son necesariamente no periódicos, exactamente de la misma manera que se describió anteriormente, pero el mosaico de la silla en sí no es aperiódico; es fácil encontrar mosaicos periódicos con mosaicos de silla sin marcar.

El sistema de teselado de sustitución de la silla

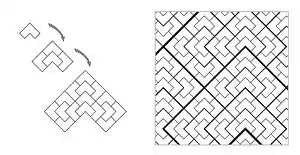
Sin embargo, los mosaicos que se muestran a continuación fuerzan a emerger la estructura de sustitución de la silla, por lo que son aperiódicos.[14]

Las teselas trilobites y cruz hacen cumplir la estructura de sustitución de la silla: solo pueden admitir teselaciones en las que se pueda discernir la sustitución de la silla y, por lo tanto, sean aperiódicas

Los mosaicos de Penrose, y poco después los diferentes conjuntos de mosaicos de Amán,[15] fueron el primer ejemplo basado en forzar explícitamente la aparición de una estructura de mosaico de sustitución. Joshua Socolar,[16][17] Roger Penrose,[18] Ludwig Danzer,[19] y Chaim Goodman-Strauss[14] han encontrado varios conjuntos posteriormente. Shahar Mozes dio la primera construcción general, mostrando que todos los productos de los sistemas de sustitución unidimensionales se pueden aplicar mediante reglas de coincidencia.[13] Charles Radin encontró reglas que hacen cumplir el sistema teselados de sustitución del molinillo de Conway.[20] En 1998, Goodman-Strauss mostró que se pueden encontrar reglas de emparejamiento locales para forzar cualquier estructura de mosaico de sustitución, sujeto a algunas condiciones leves.[12]

Método de cortar y proyectar

Los mosaicos no periódicos también se pueden obtener mediante la proyección de estructuras de mayor dimensión en espacios con menor dimensión, y en algunas circunstancias, puede haber mosaicos que refuercen esta estructura no periódica, y por lo tanto, sean aperiódicos. Los mosaicos de Penrose son el primer y más famoso ejemplo de esto, como se señaló por primera vez en el trabajo pionero de de Bruijn.[21] Aún no existe una caracterización completa (algebraica) de los mosaicos de corte y proyección que se pueda hacer cumplir mediante reglas de coincidencia, aunque se conocen numerosas condiciones necesarias o suficientes.[22]

Algunas teselaciones obtenidas por el método de corte y proyección. Los planos de corte son todos paralelos al que define los mosaicos de Penrose (el cuarto mosaico de la tercera línea). Estos mosaicos están todos en diferentes clases de isomorfismos locales, es decir, son localmente distinguibles

Los mosaicos aperiódicos se consideraron entidades puramente matemáticas hasta 1984, cuando el físico Dan Shechtman anunció el descubrimiento de una fase de una aleación de aluminio-manganeso que produjo un difractograma nítido con una simetría quíntuple inequívoca,[3] por lo que tenía que ser una sustancia cristalina con simetría icosaédrica. En 1975, Robert Ammann ya había ampliado la construcción de Penrose a un equivalente icosaédrico tridimensional. En tales casos, el término "embaldosado" significa "llenar el espacio". Los dispositivos fotónicos se construyen actualmente como secuencias aperiódicas de diferentes capas, siendo así aperiódicas en una dirección y periódicas en las otras dos. Las estructuras cuasicristalinas de Cd-Te parecen consistir en capas atómicas en las que los átomos están dispuestos en un patrón aperiódico plano. A veces se produce un mínimo energético o un máximo de entropía para tales estructuras aperiódicas. Steinhardt ha demostrado que los decágonos superpuestos de Gummelt permiten la aplicación de un principio extremo y, por lo tanto, proporcionan el vínculo entre las matemáticas del revestimiento aperiódico y la estructura de los cuasicristales.[28] Se ha observado que las ondas de Faraday forman grandes zonas de patrones aperiódicos.[29] La física de este descubrimiento ha revivido el interés en estructuras y frecuencias inconmensurables que sugieren vincular teselaciones aperiódicas con fenómenos de interferencia.[30]

El término aperiódico se ha utilizado en una amplia variedad de formas en la literatura matemática sobre teselaciones (y también en otros campos matemáticos, como los sistemas dinámicos o la teoría de grafos, con significados completamente diferentes). Con respecto a las teselaciones, el término aperiódico se utilizó a veces como sinónimo del término no periódico. Un mosaico "no periódico" es simplemente uno que no está fijado por ninguna traslación no trivial. A veces, el término describe, implícita o explícitamente, un mosaico generado por un conjunto aperiódico de prototeselas. Con frecuencia, el término aperiódico se usó vagamente para describir las estructuras en consideración, refiriéndose a sólidos físicos aperiódicos, a saber, cuasicristales, o algo no periódico con algún tipo de orden global.

El uso de la palabra mosaico también es problemático, a pesar de su sencilla definición. No hay una sola teselación de Penrose, por ejemplo: los rombos de Penrose admiten infinitas teselaciones (que no se pueden distinguir localmente). Una solución común es tratar de usar los términos con cuidado en la redacción técnica, pero reconociendo el uso generalizado de los términos informales.

• Teselas girih
• Anexo:Conjuntos de teselas aperiódicos
• Cuasicristal
• Zellige

• The Geometry Junkyard
• Tilings aperiódicos
• El patrón infinito que nunca se repite