Tetraedro ortocéntrico
En geometría, un tetraedro ortocéntrico, es un tetraedro cuyas cuatro alturas son concurrentes. Su punto de convergencia se designa entonces como el ortocentro del tetraedro.
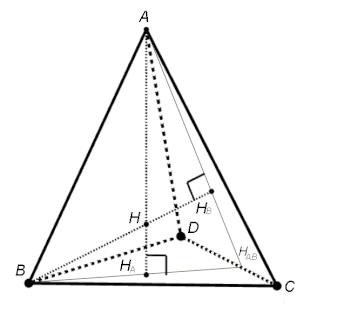
Fue estudiado por Simon Lhuilier en 1782[1] y más adelante por G. de Longchamps en 1890, quien le dio el nombre.[2]
El tetraedro regular y el tetraedro trirrectangular son casos especiales de tetraedro ortocéntrico, pero no así el tetraedro cuatrirrectángulo.
Propiedades
Ortogonalidad de aristas opuestas
Un tetraedro es ortocéntrico si y solo si sus aristas opuestas son ortogonales dos a dos.[3]
| Demostración |
Sean los pies de las alturas provenientes de . Por hipótesis, los segmentos y se cruzan en . Forman el plano que contiene los 4 puntos . Por otra parte, es ortogonal al plano , por tanto a cualquier normal de este plano, y en particular a . De manera similar, es ortogonal a , por lo que el plano es ortogonal a . Se deduce que es ortogonal a y se hace lo mismo con los demás pares de aristas.
Sean los ortocentros de las caras opuestas a los índices. Siendo los dos segmentos que se cruzan y ortogonales a , el plano también es ortogonal a , y lo mismo el plano . Los planos y , ortogonales a una misma recta y que tienen un punto en común, son el mismo. Por lo tanto, las rectas y de este plano se cortan en un punto . La recta del plano es ortogonal a , y de manera similar se demostraría que es ortogonal a . Por lo tanto, es ortogonal al plano , es decir, es la altura que viene de . Asimismo, es la altura de y estas dos alturas se cruzan. Por simetría, las cuatro alturas son entonces secantes dos a dos, y por lo tanto concurrentes porque no son coplanares. |
Además, la denominada relación de Euler[3] implica que basta con que dos pares de aristas opuestas sean ortogonales para que los tres pares lo sean también.
Pies de las alturas
Un tetraedro es ortocéntrico si y solo si los pies de las cuatro alturas son los ortocentros de las caras, y basta que un pie de altura lo sea para que el tetraedro sea ortocéntrico[3].
| Demostración |
Volviendo a la demostración anterior, la recta del plano ortogonal a es ortogonal a ; es por tanto la altura procedente de en el triángulo . Pero por simetría de las hipótesis, las rectas y son las otras dos alturas del triángulo : es, por tanto, el ortocentro, y lo mismo para .
Sea el ortocentro de . El plano contiene las rectas y que son ortogonales a , por lo tanto es ortogonal a . La recta que está en este plano es por tanto ortogonal a y se podría hacer lo mismo con los demás pares de aristas opuestas. |
Por lo tanto, se obtiene cualquier tetraedro ortocéntrico partiendo de un triángulo y tomando el cuarto vértice en la perpendicular al plano de este triángulo que pasa por el ortocentro.
Paralelepípedo circunscrito
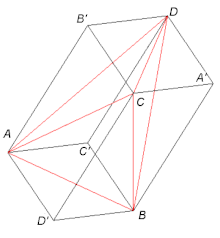
Es posible inscribir un tetraedro en el paralelepípedo cuyos tres pares de caras paralelas estén incluidos en los pares de planos paralelos que contienen dos aristas opuestas.
Un tetraedro es ortocéntrico si y solo si este paralelepípedo circunscrito tiene sus aristas de la misma longitud, en otras palabras es un romboedro.
De hecho, en el tetraedro, dos aristas opuestas son ortogonales si y solo si las caras correspondientes del paralelepípedo circunscrito son rombos (porque un paralelogramo es un rombo si y solo si sus diagonales son ortogonales). Si cuatro caras de un paralelepípedo son rombos, entonces todas las aristas tienen longitudes iguales y las seis caras son rombos. De ello se deduce que si dos pares de aristas opuestas en un tetraedro se forman a partir de aristas ortogonales, entonces el tercer par tiene la misma propiedad y el tetraedro es ortocéntrico.
Relación métrica
Un tetraedro “ABCD” es ortocéntrico si y solo si la suma de los cuadrados de las longitudes de dos aristas opuestas es la misma para los tres pares de aristas opuestas:[4][5][3]
De hecho, basta con que solo dos pares de aristas opuestas satisfagan esta condición para que el tetraedro sea ortocéntrico.
| Demostración |
|
Entonces, si y solo si las aristas y son ortogonales. Escribiendo la misma relación para las aristas y , se obtiene que esta condición es necesaria y suficiente. |
Bimedianas
Un tetraedro es ortocéntrico si y solo si sus tres bimedianas (que unen los puntos medios de dos aristas opuestas) tienen la misma longitud.[5][3]
En efecto, las bimedianas son los segmentos que unen los centros de dos caras opuestas del paralelepípedo circunscrito, que tienen la misma longitud que las aristas paralelas a ellas. Por lo tanto, tienen la misma longitud si y solo si las aristas del paralelepípedo tienen la misma longitud.

Bialturas
En un tetraedro ortocéntrico, las bialturas (perpendiculares comunes a dos aristas opuestas) coinciden en el ortocentro.
| Demostración |
|
El punto pertenece al plano que es el plano que contiene a y ortogonal a . A su vez, también pertenece al plano , que es el plano que contiene a y ortogonal a , y por lo tanto pertenece a su intersección que es la bialtura perpendicular común a y . Asimismo, pertenece a las otras dos bialturas. |
Por el contrario, un tetraedro cuyas bialturas son concurrentes es ortocéntrico, equifacial, o está formado por un diamante oblicuo y sus diagonales[6][7][8].
Punto de Monge y recta de Euler
Se tiene el siguiente teorema, debido a Gaspard Monge:
|
Si el tetraedro no es equifacial, en cuyo caso O=G, estos tres puntos están alineados en la denominada recta de Euler por analogía con el caso del triángulo. Y cuando el tetraedro es ortocéntrico, el punto de Monge coincide con el ortocentro.[9][10]
| Demostración |
|
Se dispone como el simétrico de con respecto a . Sean I y J los respectivos puntos medios de [AB] y [CD]. Entonces, se demuestra que . Como (OJ) es ortogonal a (CD), esto demuestra que el plano que pasa por y es ortogonal a pasa por y, por simetría, la misma propiedad se cumple para los seis planos similares. Se puede afirmar que: ; o , por lo tanto y . Si el tetraedro es ortocéntrico, el plano que pasa por el centro de y ortogonal a es el plano que contiene a y ortogonal a . Razonando de la misma manera para el plano que pasa por el medio de y ortogonal a , se obtiene que el punto pertenece a su intersección, que es la bialtura asociada a y . Pertenece por tanto a las tres bialturas, que coinciden en . Entonces, . |
Esferas de Euler
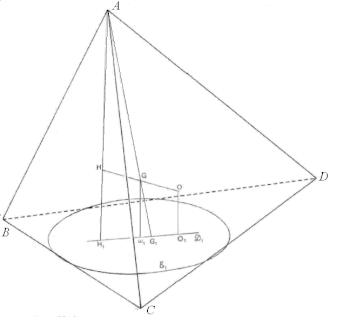
Primera esfera de Euler
Los cuatro puntos medios de las aristas y los ocho pies de las perpendiculares comunes a las aristas opuestas son doce puntos de una misma esfera de centro G. Las intersecciones de la esfera con las caras son sus círculos de Euler.[11][3]
Segunda esfera de Euler
Los cuatro puntos ubicados en el tercio de los segmentos que unen H con los vértices, los cuatro pies de las alturas y los cuatro centros de gravedad de las caras son doce puntos de la misma esfera centrada en la recta de Euler en O', que verifica . Es la imagen de la esfera circunscrita[11][3] por la homotecia con centro G y razón -1/3.
Volumen del tetraedro ortocéntrico
Una primera fórmula es:
donde a, b son las longitudes de dos aristas opuestas y su distancia.[11]
Las propiedades de las aristas implican que si solo cuatro de las seis aristas de un tetraedro ortocéntrico son de longitud conocida, se pueden calcular las longitudes de las otras dos si no son opuestas entre sí. Por lo tanto, el volumen de un tetraedro ortocéntrico se puede expresar en términos de cuatro longitudes de aristas a, b, c, a'.
La fórmula es:[12]
donde a, b, c son las longitudes de las aristas de una misma cara, es el semi perímetro de esta cara y a' es la longitud de la arista opuesta a la de longitud a.
Artículos relacionados
- Disfenoide
- Tetraedro trirrectangular
- Cuadrángulo ortocéntrico, un tetraedro ortocéntrico aplanado
Referencias
- N. A. Court (Octobre 1934). «Notes on the Orthocentric Tetrahedron». The American Mathematical Monthly (en inglés) 41 (8): 499-502.
- G. de Longchamps (1890). «Le tétraèdre orthocentrique». Mathesis: 50.
- Yves Ladegaillerie (2003). «379-382». En Ellipses, ed. Géométrie, affine, projective, euclidienne, et anallagmatique.
- Reiman, István, "International Mathematical Olympiad: 1976-1990", Anthem Press, 2005, pp. 175-176.
- Hazewinkel, Michiel, "Encyclopaedia of mathematics: Supplement, Volym 3", Kluwer Academic Publishers, 1997, p. 468.
- E. Ehrhart (1985). «75-76». En Cedic/Nathan, ed. Articles de mathématiques [Sur les tétraèdres dont les perpendiculaires communes aux arêtes opposées sont concourantes].
- E. Ehrhart (Nov/Dec 1991). «Sur le triangle et le tétraèdre». Bulletin de l'APMEP (381): 621.
- Bertrand Gambier (1948). «Sur les tétraèdres dont certaines bihauteurs se rencontrent». Bulletin de la S. M. F. 76: 79-94.
- Victor Thébault (1955). «2 - 10». En Librairie Vuibert, ed. Parmi les belles figures de la géométrie dans l'espace : géométrie du tétraèdre. Paris.
- Tristan Deray (Juin 2009). «Point de Monge au lycée, plaisir et délectation géométrique.». Feuille de vigne: 15-20.
- Yvonne et René Sortais (1988). «315-329». En Hermann, ed. Géométrie de l'espace et du plan.
- Andreescu, Titu and Gelca, Razvan, "Mathematical Olympiad Challenges", Birkhäuser, second edition, 2009, pp. 30-31, 159.