Transformación activa y pasiva
En física e ingeniería, una transformación activa o transformación coartada,[1] es una transformación que en realidad cambia la posición física de un punto, o cuerpo rígido, que se puede definir incluso en la ausencia de un sistema de coordenadas; mientras que una transformación pasiva o transformación alias,[2] no es más que un cambio en el sistema de coordenadas en el que el objeto se describe (cambio de coordenadas del mapa, o cambio de base). De manera predeterminada, por transformación, los matemáticos por lo general se refieren a transformaciones activas, mientras que los físicos e ingenieros usan ambas.
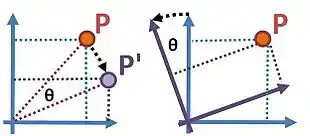
Dicho de otra manera, una transformación pasiva se refiere a la descripción del "mismo objeto" en dos sistemas de coordenadas diferentes.[3] Por otro lado, una transformación activa es una transformación de uno o varios objetos con respecto al mismo sistema de coordenadas. Por ejemplo, las transformaciones activas son útiles para describir las posiciones sucesivas de un cuerpo rígido. Las transformaciones pasivas pueden ser útiles en análisis de movimiento humano para observar el movimiento de la tibia en relación con el fémur, es decir, su movimiento con respecto a un sistema de coordenadas (local) que se mueve junto con el fémur, en lugar de un sistema (global) de coordenadas que se fija al suelo.[3]
Ejemplo
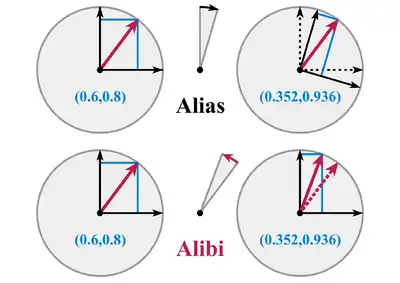

A modo de ejemplo, en el espacio vectorial ℝ2 , sea { e1 , e2 } una base, y considerar el vector v = v1 e1 + v 2 e2 . La rotación del vector a través de θ ángulo viene dada por la matriz de rotación:
que se puede ver ya sea como una transformación activa o una transformación pasiva (en la que se invierte la matriz anterior), como se describe a continuación.
Transformación activa
Como una transformación activa, R hace girar el vector inicial v, y se obtiene un nuevo vector v'. Para una rotación en sentido antihorario de v con respecto al sistema de coordenadas fijo:
Si uno ve {R e1 , R e2 } como una nueva base, entonces las coordenadas del nuevo vector v' en la base nueva son las mismas que las de v en la base original. Debe tenerse en cuenta que las transformaciones activas tienen sentido, incluso como una transformación lineal en un espacio vectorial diferente. Tiene sentido para escribir el nuevo vector en la base sin imprimación (como anteriormente) solo cuando la transformación es desde el espacio en sí mismo.
Transformación pasiva
Por otro lado, cuando se ve R como una transformación pasiva, el vector inicial v se deja sin cambios, mientras que el sistema de coordenadas y sus vectores base se giran. Con el fin de que el vector se mantenga fijo, las coordenadas en términos de la nueva base deben cambiar. Para un giro hacia la izquierda de los sistemas de coordenadas:
De esta ecuación se ve que las nuevas coordenadas (es decir, las coordenadas con respecto a la nueva base) son dadas por
así que esto se puede escribir como
Por lo tanto, para que el vector se mantenga sin cambios por la transformación pasiva, las coordenadas del vector deben transformarse de acuerdo con la inversa del operador de transformación activa.[4]
Véase también
Referencias
- Weisstein, Eric W. "Alibi Transformación". De MathWorld - Un recurso Wolfram Web
- Weisstein, Eric W. "Transformación Alias". De MathWorld -. Un recurso Wolfram Web
- Joseph K. Davidson, Kenneth Henderson Hunt (2004). «§4.4.1 The active interpretation and the active transformation». Robots and screw theory: applications of kinematics and statics to robotics. Oxford University Press. p. 74 ff. ISBN 0-19-856245-4.
- Amidror, Isaac (2007). «Appendix D: Remark D.12». The theory of the Moiré phenomenon: Aperiodic layers. Springer. p. 346. ISBN 1-4020-5457-2.
- Dirk Struik (1953) Lectures on Analytic and Projective Geometry, página 84, Addison-Wesley.
Enlaces externos
- Esta obra contiene una traducción derivada de «Active and passive transformation» de Wikipedia en inglés, concretamente de esta versión, publicada por sus editores bajo la Licencia de documentación libre de GNU y la Licencia Creative Commons Atribución-CompartirIgual 4.0 Internacional.