Sistema de coordenadas
En geometría, un sistema de coordenadas es un sistema de referencia que utiliza uno o más números (coordenadas) para determinar unívocamente la posición de un punto u objeto geométrico.[1] El orden en que se escriben las coordenadas es significativo y a veces se las identifica por su posición en una tupla ordenada; también se las puede representar con letras, como por ejemplo «la coordenada-x». El estudio de los sistemas de coordenadas es el objeto de la geometría analítica, que permite formular problemas geométricos de forma "numérica".[2]
Introducción
Coordenadas en geometría
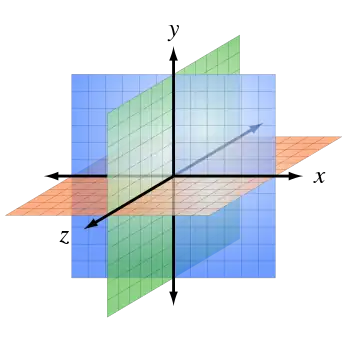
En geometría, las coordenadas son valores numéricos que determinan la posición de un punto en un plano o en el espacio. En un plano euclídeo, la posición de un punto puede venir determinada por las distancias a dos líneas rectas (ejes de coordenadas) que se cruzan en un punto (origen) en ángulo recto; una de las coordenadas se llama ordenada y la otra abscisa. En el espacio euclídeo tridiomensional según el sistema de Descartes, la posición de un punto está determinada si se sepecifican las distancias a tres planos de coordenadas que se cruzan en un punto en ángulo recto entre sí. Sin embargo estas formas de especificar un punto no son las únicas posibles, las coordenadas polares en el plano o las coordenadas esféricas (donde el origen está en el centro de una serie de esferas) o las coordenadas cilíndricas en el espacio son otras formas que requieren especificar menos distancias y más ángulos de orientación.
En geografía, las coordenadas se eligen como un sistema de coordenadas aproximadamente esférico: latitud, longitud y altura por encima de un nivel general conocido (como por ejemplo, el del océano). La latitud mide la ubicación norte-sur de un punto en relación con el ecuador, la longitud mide la ubicación este-oeste en relación con el meridiano de Greenwich, y la altura representa la elevación de un punto sobre un nivel de referencia, como el nivel del mar. Este sistema de coordenadas es esencial para la ubicación precisa en la superficie terrestre y se utiliza en cartografía, navegación, topografía y en tecnologías GNSS (Sistema Global de Navegación por Satélite), proporcionando una base sólida para la representación geoespacial y la geolocalización precisa de lugares en todo el mundo.
El sistema de coordenadas más utilizado es el sistema de coordenadas rectangulares, también conocido como sistema de coordenadas cartesianas. Ese tipo de sistemas puede funcionar como un sistema de coordenadas único para todo un espacio euclídeo y los puntos y objetos situados dentro de él. Para lograr eso se requiere la noción de origen de coordenadas.
Las coordenadas en el plano y en el espacio se pueden definir de un número ilimitado de formas diferentes. La resolución de numerosos problemas matemáticos o físicos implica elegir aquel sistema de coordenadas específico en el que el problema se resuelva más fácil o más conveniente en cada caso particular.
Coordenadas en física y astronomía
En astronomía, las coordenadas celestes son un par ordenado de cantidades angulares (por ejemplo, ascensión recta y declinación), con las que se determina la posición de distintos puntos luminosos y de puntos auxiliares en la esfera celeste. En la práctica, se utilizan varios sistemas de coordenadas celestes. Cada uno de ellos es esencialmente un sistema de coordenadas esféricas (sin coordenadas radiales) con un plano fundamental y un origen elegidos apropiadamente. Dependiendo de la elección del plano fundamental, el sistema de coordenadas celestes se llama horizontal (plano del horizonte), ecuatorial (plano ecuatorial), eclíptico (plano de la eclíptica) o galáctico (plano galáctico). El concepto de sistemas de coordenadas aplica a espacios geométricos más complejos que el espacio euclídeo, por esa razón se requiere una definición formal de sistema de coordenadas que especifique la posición de puntos. Nótese que por ejemplo de acuerdo a la cosmología moderna la forma del espacio-tiempo es un espacio curvado por lo que en el universo no siempre sería posible usar coordenadas cartesianas.
Definición formal
Dado un espacio geométrico o topológico que tiene estuctura de variedad diferenciable de dimensión n un sistema de coordenadas es una difeomorfismo: , donde es un conjunto abierto del espacio euclídeo n-dimensional. Es decir, para cada punto tenemos las coordenadas , el conjunto de todas estas n-tuplas para el espacio define un sistema de coordenadas local.
Ejemplos de sistemas de coordenadas
Sistema coordenado lineal
Es el conjunto de los números reales representado gráficamente por una recta en la que se pueden ubicar todos los números naturales, enteros, fraccionarios, decimales, etc.[3]
Cada punto de la recta representa un número real, ya sea mediante una correspondencia biunívoca o mediante una aplicación biyectiva, usada para representar los números como puntos especialmente marcados, como por ejemplo los números enteros mediante una recta llamada recta graduada como la entera[3] de puntos ordenados y separados entre sí a la misma distancia. El punto que representa el cero () es el punto de referencia principal del sistema de coordenadas, llamado punto de origen.
Tomando en cuenta que cada uno de los puntos de la recta representa gráficamente un número real, a la derecha del punto origen se hallan todos los números reales positivos y a la izquierda todos los números reales negativos.[4]
Para representar un número de la recta real se emplean las letras mayúsculas y sus coordenadas correspondientes, por ejemplo, los puntos A(5), B(3), C(-3), D(-5),etc.

Sistema de coordenadas cartesianas
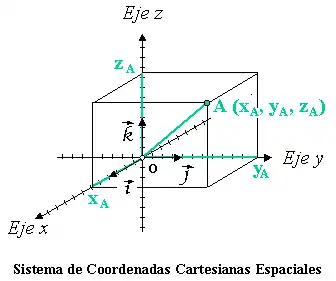
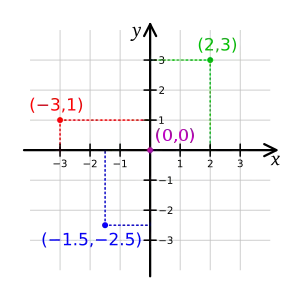
En un espacio euclídeo, un sistema de coordenadas cartesianas se define por dos o tres ejes ortogonales igualmente escalados, dependiendo de si es un sistema bidimensional o tridimensional (análogamente en se pueden definir sistemas n-dimensionales). El valor de cada una de las coordenadas de un punto (A) es igual a la proyección ortogonal del vector de posición de dicho punto () sobre un eje determinado:
Cada uno de los ejes está definido por un vector director y por el origen de coordenadas. Por ejemplo, el eje x está definido por el origen de coordenadas (O) y un vector () tal que:
- , cuyo módulo es .
El valor de la coordenada x de un punto es igual a la proyección ortogonal del vector de posición de dicho punto sobre el eje x:
Sistema de coordenadas polares
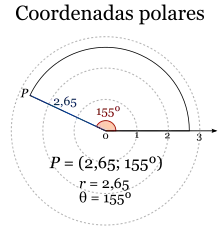
Las coordenadas polares son un sistema de coordenadas bidimensional en el que cada punto o posición del plano se determina mediante un ángulo y una distancia.[5]
Se elige un punto como polo y se toma una semirrecta desde este punto como eje polar. Para un ángulo dado , hay una única línea recta que pasa por el polo cuyo ángulo con el eje polar es (medido en sentido contrario al de las agujas del reloj desde el eje hasta la línea). Entonces hay un único punto en esta línea cuya distancia con signo al origen es r para un número dado r. Para un par de coordenadas dado hay un único punto, pero cualquier punto está representado por muchos pares de coordenadas. Por ejemplo, , y son todas coordenadas polares para el mismo punto. El polo está representado por para cualquier valor de .
Sistema de coordenadas log-polares
Es un sistema de coordenadas donde un punto se identifica con dos números, uno para el logaritmo de la distancia a un cierto punto y otro para un ángulo. Las coordenadas logarítmicas están estrechamente conectadas con las coordenadas polares, que generalmente se usan para describir dominios en el plano con algún tipo de simetría rotacional.
Sistema de coordenadas cilíndricas
 Sistema de coordenadas cilíndricas |
 Significado de las coordenadas cilíndricas |
El sistema de coordenadas cilíndricas se usa para representar los puntos de un espacio euclídeo tridimensional. Resulta especialmente útil en problemas con simetría axial. Este sistema de coordenadas es una generalización del sistema de coordenadas polares del plano euclídeo, al que se añade un tercer eje de referencia ortogonal a los otros dos. La primera coordenada es la distancia existente entre el eje y el punto, la segunda es el ángulo que forman el eje y la recta que pasa por ambos puntos, mientras que la tercera es la coordenada que determina la altura del cilindro.
Sistema de coordenadas esféricas
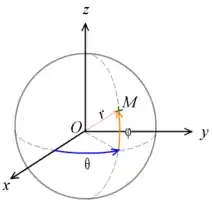 Coordenadas esféricas |
 Coordenadas geográficas |
Al igual que las coordenadas cilíndricas, el sistema de coordenadas esféricas se usa en espacios euclidianos tridimensionales. Este sistema de coordenadas esféricas está formado por tres ejes mutuamente ortogonales que se cortan en el origen. La primera coordenada es la distancia entre el origen y el punto, siendo las otras dos los ángulos que es necesario girar para alcanzar la posición del punto.
Coordenadas geográficas
Este tipo de coordenadas cartográficas, subtipo de las coordenadas esféricas, se usa para definir puntos sobre una superficie esférica. Hay varios tipos de coordenadas geográficas. El sistema más clásico y conocido es el que emplea la latitud y la longitud, que pueden mostrase en los siguientes formatos:
- DD — Decimal Degree (Grados Polares): ej. 49.500-123.500
- DM — Degree:Minute (Grados:Minutos): ej. 49:30.0-123:30.0
- DMS — Degree:Minute:Second (Grados:Minutos:Segundos): ej. 49:30:00-123:30:00
También se pueden definir las coordenadas de un punto de la superficie de la Tierra utilizando una proyección cartográfica. El sistema de coordenadas cartográficas proyectadas más habitual es el sistema de coordenadas UTM.
Coordenadas curvilíneas generales
Un sistema de coordenadas curvilíneos es la forma más general de parametrizar o etiquetar los puntos de un espacio localmente euclídeo o de una variedad diferenciable (globalmente, el espacio puede ser euclídeo, pero no necesariamente). Si se trata de un espacio localmente euclídeo de dimensión , se puede construir un sistema de coordenadas curvilíneo local en torno a un punto siempre a partir de cualquier difeomorfismo que cumpla:
Para cualquier punto q cercano a p se definen sus coordenadas curvilíneas como:
Si el espacio localmente euclídeo tiene la estructura de variedad de Riemann se pueden clasificar ciertos sistemas de coordenadas curvilíneas como sistemas de coordenadas ortogonales o incluso como sistemas de coordenadas ortonormales. Las coordenadas cilíndricas y las coordenadas esféricas son casos particulares de sistemas de coordenadas ortogonales sobre el espacio euclídeo .
Coordenadas curvilíneas ortogonales
Un sistema de coordenadas curvilíneas se llama ortogonal cuando el tensor métrico expresado en esas coordenadas tiene una forma diagonal. Cuando eso sucede muchas de las fórmulas del cálculo vectorial diferencial se pueden escribir de forma particularmente simple en esas coordenadas, pudiéndose aprovechar ese hecho cuando existe por ejemplo simetría axial, esférica o de otro tipo fácilmente representable en esas coordenadas curvilíneas ortogonales.
Las coordenadas esféricas y cilíndricas son casos particulares de coordenadas curvilíneas ortogonales.
Coordenadas homogéneas
En matemáticas, y más concretamente en geometría proyectiva, las coordenadas homogéneas son un instrumento usado para describir un punto en el espacio proyectivo. Fueron introducidas por el matemático alemán August Ferdinand Möbius en el año 1837.
También pueden usarse como un sistema alternativo de coordenadas para trabajar en el espacio euclídeo, pues este puede verse como un subconjunto del espacio proyectivo. De ese modo, las coordenadas homogéneas son ampliamente usadas en infografía para la representación de escenas en tres dimensiones. Su notación en forma matricial se emplea en bibliotecas de programación gráfica en 3D como OpenGL y Direct3D.
En coordenadas homogéneas, todo punto bidimensional está definido por tres coordenadas, de tal modo que un punto de dimensiones , se representa por la terna
Las coordenadas en dos dimensiones se pueden encontrar más fácilmente si , por simplificación. En tres dimensiones, suele ocurrir lo mismo.[6][7]
Una consecuencia de esta escritura es que un punto propio tiene infinitas formas de escribirse, pues está determinado por una relación de equivalencia entre el punto en cuestión y aquellos otros contenidos en la recta que genera.
La idea básica se trata de ampliar el plano euclídeo (en el caso bidimensional) al plano proyectivo. Esto implica la consideración de los puntos impropios, o del infinito. Un punto impropio es aquel donde λ = 0, y está determinado por la dirección de una recta, contenida en el plano proyectivo.[8]
Otros sistemas de uso común
Algunos otros sistemas de coordenadas comunes son los siguientes:
- Coordenadas curvilíneas son una generalización de los sistemas de coordenadas en general; el sistema se basa en la intersección de curvas.
- Coordenadas ortogonales: Las superficies de coordenadas se encuentran en ángulos rectos.
- Coordenadas oblicuas: Las superficies de coordenadas no son ortogonales.
- El sistema de coordenadas log-polar representa un punto en el plano por el logaritmo de la distancia al origen y un ángulo medido desde una línea de referencia que interseca el origen.
- Las coordenadas plückerianas son una forma de representar líneas en el espacio euclídeo tridimensional utilizando una sexta pareja de números como coordenadas homogéneas.
- Coordenadas generalizadas se utilizan en el tratamiento de la mecánica lagrangiana.
- Las coordenadas canónicas se utilizan en el tratamiento de la mecánica hamiltoniana.
- Las coordenadas baricéntricas (n-simplex) se utilizan para representar diagramas ternarios y más generalmente en el análisis de triángulos. Fueron introducidas por primera vez por August Möbius, quien resolvió la cuestión sobre el centro de gravedad de las masas situadas en los vértices del triángulo. Son invariantes afines, representando un caso especial de las coordenadas generales homogéneas. Un punto con coordenadas baricéntricas se encuentra en un espacio vectorial -dimensional , y las coordenadas reales en este caso se refieren a un sistema fijo de puntos que no se encuentran en el subespacio -dimensional. Las coordenadas baricéntricas también se utilizan en topología algebraica con respecto a los puntos del simplex.[9]
- Las coordenadas trilineales son una de las muestras de coordenadas homogéneas y se basan en un triángulo dado, de modo que la posición de un punto se determina en relación con los lados de este triángulo, principalmente por el valor de la distancia desde ellos, aunque son posibles otras variaciones. Las coordenadas trilineales se pueden convertir a coordenadas baricéntricas con relativa facilidad; además, también son convertibles en coordenadas rectangulares bidimensionales, para lo que se utilizan las fórmulas correspondientes. Se utilizan en el contexto de los triángulos.[10]
- Coordenadas biangulares. En matemáticas, las coordenadas biangulares son un sistema de coordenadas del plano donde y son dos puntos fijos, y la posición de un punto P no alineado con está determinada por los ángulos y . Este tipo de coordenadas fue examinado por primera vez por Lazare Carnot, quien publicó sus resultados en 1803.[11]
- Coordenadas bipolares. Son un sistema de coordenadas ortogonales bidimensional, basado en las circunferencias de Apolonio.[12] Confusamente, el mismo término también se usa a veces para designar a las coordenadas bicéntricas. Además, existe un tercer sistema también basado en dos polos (las coordenadas biangulares).
- Las coordenadas bicéntricas, (también denominadas coordenadas bipolares de dos centros) son un sistema de coordenadas, basado en dos coordenadas que dan las distancias desde dos centros fijos, y .[12] Este sistema es muy útil en algunas aplicaciones científicas (como por ejemplo, calcular el campo eléctrico de un dipolo en un plano).[13][14]
- Coordenadas cónicas: Son un sistema de tres dimensiones ortogonales que consta de esferas concéntricas, que se describen por su radio, y dos familias de conos perpendiculares situados a lo largo de los ejes .
- Coordenadas parabólicas: Son un sistema de coordenadas ortogonales bidimensionales en el que las líneas de coordenadas son parábolas confocales. Una versión tridimensional de coordenadas parabólicas se obtine mediante la rotación del sistema bidimensional sobre el eje de simetría de las parábolas. Las coordenadas parabólicas son útiles en muchas aplicaciones, como por ejemplo, en el tratamiento del efecto Stark y en la teoría del potencial de los bordes.
- Coordenadas proyectivas. Se denominan de acuerdo con el espacio proyectivo sobre el que se definen, y representan una correspondencia biunívoca entre sus elementos y clases de subconjuntos finitos de elementos del cuerpo , caracterizados por las propiedades de equivalencia y ordenamiento. Para determinar las coordenadas proyectivas de los subespacios proyectivos, es suficiente determinar las coordenadas correspondientes de los puntos del espacio proyectivo. En el caso general, con respecto a alguna base, las coordenadas proyectivas se introducen por medios puramente proyectivos.[15]
- Las coordenadas de Rindler se utilizan principalmente en el marco de la teoría de la relatividad y describen esa parte del espacio-tiempo plano, que generalmente se llama espacio de Minkowski. En la teoría especial de la relatividad, una partícula que se acelera uniformemente está en movimiento hiperbólico, y para cada una de esas partículas en las coordenadas de Rindler se puede elegir un punto de referencia en relación con el que está en reposo.
- Un sistema de coordenadas toroidales es un sistema de coordenadas ortogonales tridimensionales que se obtiene al girar un sistema de coordenadas bipolares bidimensionales alrededor de un eje que separa sus dos focos. Los focos del sistema bipolar, respectivamente, se convierten en un anillo con radio , que se encuentra en el plano del sistema de coordenadas toroidales, mientras que el eje se convierte en el eje de rotación del sistema. El anillo focal también se denomina a veces círculo base.[16]
- Coordenadas parabólicas cilíndricas: Son un sistema de coordenadas ortogonales tridimensionales obtenido como resultado de una transformación espacial de un sistema de coordenadas parabólicas bidimensionales. Las superficies de revolución parabólicas confocales, respectivamente, sirven como superficies coordenadas. Las coordenadas parabólicas cilíndricas están relacionadas con las coordenadas rectangulares de cierta manera y se pueden aplicar en varias áreas de la investigación científica.[17]
Hay formas de describir curvas sin coordenadas, utilizando ecuaciones intrínsecas que usan cantidades invariantes como la curvatura y la longitud de arco. Estas incluyen:
- La ecuación de Whewell relaciona la longitud de arco y el ángulo tangencial.
- La ecuación de Cesàro relaciona la longitud de arco y la curvatura.
Coordenadas de objetos geométricos
Los sistemas de coordenadas suelen utilizarse para especificar la posición de un punto, pero también pueden utilizarse para especificar la posición de figuras más complejas como rectas, planos, círculos o esferas. Por ejemplo, las coordenadas plückerianas permiten determinar la posición de una línea recta en el espacio.[18] Cuando es necesario, el tipo de figura que se describe se utiliza para distinguir el tipo de sistema de coordenadas, por ejemplo el término coordenadas de la recta se utiliza para cualquier sistema de coordenadas que especifica la posición de una línea recta.
Puede ocurrir que los sistemas de coordenadas para dos conjuntos diferentes de figuras geométricas sean equivalentes en términos de su análisis. Un ejemplo de ello son los sistemas de coordenadas homogéneos para puntos y rectas en el plano proyectivo. Los dos sistemas en un caso como este se dice que son duales. Los sistemas duales tienen la propiedad de que los resultados de un sistema pueden trasladarse al otro, ya que estos resultados son solo interpretaciones diferentes del mismo resultado analítico; esto se conoce como el principio de dualidad.[19]
Cambios de coordenadas
En la resolución de problemas físicos y matemáticos es común la estrategia del cambio de coordenadas. En esencia un cambio de coordenadas supone cambiar las variables de las que a depende el problema, a otras coordenadas diferentes en las que el problema puede tener una forma equivalente pero más simple, que permite encontrar la solución con mayor facilidad.
Dado que a menudo existen muchos sistemas de coordenadas posibles para describir figuras geométricas, es importante entender cómo se relacionan. Estas relaciones se describen mediante transformaciones de coordenadas que dan fórmulas para las coordenadas de un sistema en términos de las coordenadas de otro sistema. Por ejemplo, en el plano, si las coordenadas cartesianas y las coordenadas polares tienen el mismo origen, y el eje polar es el eje positivo de , entonces la transformación de coordenadas de las coordenadas polares a las cartesianas viene dada por .
Más formalmente un cambio de coordenadas puede representarse por un difeomorfismo o aplicación biyectiva y diferenciable (con inversa también diferenciable) entre dos conjuntos de , aquí llamados y :
Este cambio de variable permite por ejemplo reescribir integrales del siguiente modo:
Donde:
- representa la función que pretende integrarse expresada en las viejas y las nuevas coordenadas.
- es el jacobiano del cambio de coordenadas.
- es el dominio de integración expresado en las viejas y las nuevas coordenadas.
Para transformar o reescribir ecuaciones diferenciales en términos de las nuevas coordenadas se usan las leyes de transformación tensorial:
Coordenadas de líneas rectas, curvas, planos y superficies
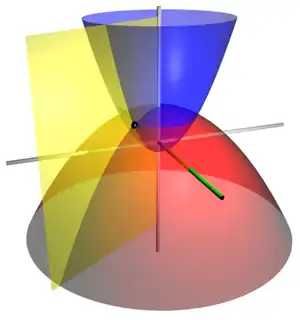
En dos dimensiones, si una de las coordenadas en un sistema de coordenadas de un punto se mantiene constante y la otra coordenada se deja variar, entonces la curva resultante se llama curva de coordenadas. En el sistema de coordenadas cartesianas las curvas de coordenadas son, de hecho, líneas rectas, por lo que son denominadas rectas coordenadas. En concreto, son las líneas paralelas a uno de los ejes de coordenadas. Para otros sistemas de coordenadas las curvas de coordenadas pueden ser curvas generales. Por ejemplo, las curvas de coordenadas en coordenadas polares obtenidas manteniendo r constante son los círculos con centro en el origen. Un sistema de coordenadas para el que algunas curvas de coordenadas no son líneas rectas se denomina sistema de coordenadas curvilíneas.[20] Este procedimiento no siempre tiene sentido, por ejemplo no existen curvas de coordenadas en los sistemas de coordenadas homogéneos.
En el espacio tridimensional, si se mantiene constante una coordenada y se permite que las otras dos varíen, la superficie resultante se llama superficie de coordenadas. Por ejemplo, las superficies de coordenadas que se obtienen manteniendo constante ρ en el sistema de coordenadas esféricas son las esferas con centro en el origen. En el espacio tridimensional la intersección de dos superficies de coordenadas es una curva de coordenadas. En el sistema de coordenadas cartesianas se puede hablar de planos de coordenadas.
Del mismo modo, las hipersuperficies de coordenadas son los espacios dimensionales que resultan de fijar una sola coordenada de un sistema de coordenadas.[21]
Origen de coordenadas

El origen de coordenadas es el punto de referencia de un sistema de coordenadas. En este punto, el valor de todas las coordenadas del sistema es nulo —por ejemplo, el en o en —. Sin embargo, en algunos sistemas de coordenadas no es necesario establecer nulas todas las coordenadas. Por ejemplo, en un sistema de coordenadas esféricas es suficiente con establecer el radio nulo , siendo indiferentes los valores de latitud y longitud.
En un sistema de coordenadas cartesianas, el origen es el punto en que los ejes del sistema se separan.
Véase también
Notas y referencias
- Weisstein, Eric W. «Coordinate System». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Weisstein, Eric W. «Coordinates». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Real Academia de Ciencias Exactas, Física y Naturales, ed. (1999). Diccionario esencial de las ciencias. Espsa. ISBN 84-239-7921-0.
- Stewart, James B.; Redlin, Lothar; Watson, Saleem (2008). College Algebra (5th edición). Brooks Cole. pp. 13-19. ISBN 978-0-495-56521-5.
- Finney, Ross; George Thomas; Franklin Demana; Bert Waits (June 1994). Calculus: Graphical, Numerical, Algebraic (Single Variable Version edición). Addison-Wesley Publishing Co. ISBN 0-201-55478-X. (requiere registro).
- David C., Lay (2007). Álgebra lineal y sus aplicaciones (3 edición). México: Pearson. pp. 159, 162. ISBN 9789702609063.
- García Alonso, Fernando Luis; Pérez Carrió, Antonio; Reyes Perales, José Antonio. Ampliación de fundamentos de matemática aplicada. España: Club Universitario. p. 110. ISBN 9788484549772.
- Santaló, Luis A. Geometría Proyectiva (3ª edición). Buenos Aires, Argentina: Eudeba. pp. 88-92.
- Sklyarenko E. (1977-1985). Coordenadas baricéntricas (Enciclopedia Matemática edición). Enciclopedia Soviética.
- Weisstein, por Eric W. Trilinear Coordinates (Ing.) En el sitio MathWorld de Wolfram
- Michael Naylor and Brian Winkel: Biangular Coordinates Redux: Discovering a New Kind of Geometry College Mathematics Journal 41:1 September 12, 2009, s. 31
- «Eric W. Weisstein, Concise Encyclopedia of Mathematics CD-ROM, Bipolar Coordinates, CD-ROM edition 1.0, May 20, 1999». Archivado desde el original el 12 de diciembre de 2007. Consultado el 2 de abril de 2019.
- R. Price, The Periodic Standing Wave Approximation: Adapted coordinates and spectral methods.
- The periodic standing-wave approximation: nonlinear scalar fields, adapted coordinates, and the eigenspectral method.
- Voitsekhovsky M.I. Coordenadas proyectivas. - Enciclopedia matemática. - M: Enciclopedia soviética, 1977-1985.
- https://mathworld.wolfram.com/ParabolicCylindricalCoordinates.html
- Hodge, W.V.D.; D. Pedoe (1994). Métodos de Geometría Algebraica, Volumen I (Libro II). Cambridge University Press. ISBN 978-0-521-46900-5.
- Woods p. 2
- Tang, K. T. (2006). Métodos matemáticos para ingenieros y científicos 2. Springer. p. 13. ISBN 3-540-30268-9.
- Liseikin, Vladimir D. (2007). A Computational Differential Geometry Approach to Grid Generation. Springer. p. 38. ISBN 978-3-540-34235-9.
Bibliografía
- Woods, Frederick S. (1922). Higher Geometry. Ginn and Co. pp. 1ff.
- Shigeyuki Morita; Teruko Nagase; Katsumi Nomizu (2001). Geometry of Differential Forms. AMS Bookstore. p. 12. ISBN 0-8218-1045-6.
- Gelfand I.M., Glagoleva E.G., Kirillov A.A. Método de coordenadas. (enlace inaccesible) Quinta edición, estereotipada. Serie: Biblioteca de la Escuela de Física y Matemáticas. Matemáticas. Edición 1.M.: Nauka, 1973.
- Delone N.B. Coordenadas en matemáticas // Diccionario enciclopédico Brockhaus y Efron : en 86 volúmenes (82 volúmenes y 4 adicionales). - SPb. , 1890-1907.
Enlaces externos
 Wikimedia Commons alberga una categoría multimedia sobre Sistema de coordenadas.
Wikimedia Commons alberga una categoría multimedia sobre Sistema de coordenadas.- Epsilones - La invención de los sistemas de coordenadas
- Hexagonal Coordinate Systems