Coordenadas bipolares
Las coordenadas bipolares son un sistema de coordenadas ortogonales bidimensional, basado en las circunferencias de Apolonio.[1] Confusamente, el mismo término también se usa a veces para designar a las coordenadas bicéntricas. Además, existe un tercer sistema también basado en dos polos (las coordenadas biangulares).
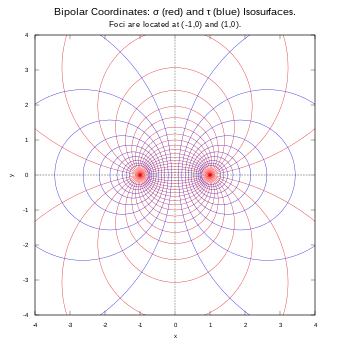
El término bipolar se usa además en ocasiones para describir otras curvas que tienen dos puntos singulares (focos), como elipses, hipérbolas y óvalos de Cassini. Sin embargo, el término coordenadas bipolares está reservado para las coordenadas que se describen aquí, y nunca se usa para sistemas asociados con esas otras curvas, como las coordenadas elípticas.
Definición
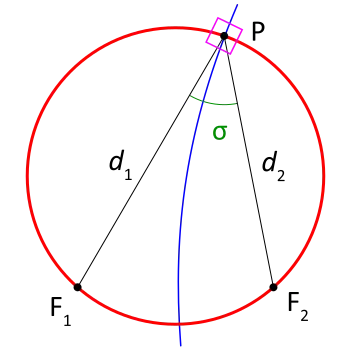
El sistema se basa en dos focos F1 y F2. Refiriéndose a la figura de la derecha, la coordenada σ de un punto P es igual al ángulo F1 P F2, y la coordenada τ es igual al logaritmo natural de la relación de las distancias d1 y d2:
Si, en el sistema cartesiano, los focos se ubican en (-a, 0) y (a, 0), las coordenadas del punto P son
La coordenada τ varía de (para puntos cercanos a F1) a (para puntos cercanos a F2). La coordenada σ solo se define en el módulo 2π, y se considera mejor que varíe de -π a π, tomándola como el negativo del ángulo agudo F1 P F2 si P está en la mitad inferior del plano.
Prueba de que el sistema de coordenadas es ortogonal
Las ecuaciones de x y y se pueden combinar para dar[2][3]
Esta ecuación muestra que σ y τ son las partes real e imaginaria de una función analítica de x + iy (con puntos de rama logarítmica en los focos), lo que a su vez demuestra (mediante la teoría general de las aplicaciones conformes) que las curvas de σ y τ se intersecan en ángulos rectos, es decir, que el sistema de coordenadas es ortogonal.
Curvas de las constantes σ y τ
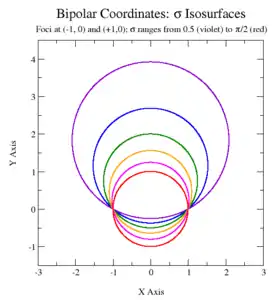
Las curvas de la constante σ corresponden a círculos no concéntricos
que se cruzan en los dos focos. Los centros de las circunferencias de la constante -σ se encuentran en el eje y. Las circunferencias de σ positivos tienen sus centros sobre el eje x, mientras que los de σ negativos se encuentran debajo del eje. Cuando la magnitud | σ | aumenta, el radio de los círculos disminuye y el centro se acerca al origen (0, 0), que se alcanza cuando | σ | = π.
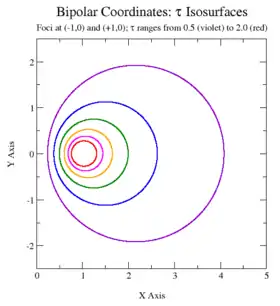
Las curvas de la constante son circunferencias no intersecantes de diferentes radios
que rodean los focos, pero que no son concéntricos. Los centros de las circunferencias de la constante -τ se encuentran en el eje x. Las circunferencias de valores de τ positivos se encuentran en el lado derecho del plano (x > 0), mientras que las circunferencias de valores de τ negativos se encuentran en el lado izquierdo del plano (x < 0). La curva de τ = 0 se corresponde con el eje y (x = 0). Cuando la magnitud de τ se incrementa, el radio de las circunferencias decrece y sus centros se aproximan a los focos (según su signo).
Relaciones recíprocas
El paso de coordenadas cartesianas a coordenadas bipolares se puede realizar a través de las siguientes fórmulas:
y
También se tienen las identidades siguientes:
y
Factores de escala
Para obtener los factores de escala de las coordenadas bipolares, se calcula la diferencial de la ecuación para , que resulta
Multiplicando esta ecuación por los complejos conjugados, se obtiene
Empleando las identidades trigométricas para productos de senos y cosenos, se obtiene
de lo que se deduce que
Por lo tanto, los factores de escala para σ y τ son iguales, y dados por
Muchos resultados desde este momento se deducen en rápida sucesión a partir de las fórmulas generales para las coordenadas ortogonales. Por lo tanto, el elemento del área infinitesimal es igual a
y el laplaciano viene dado por
Las expresiones para , y se pueden expresar obteniendo los factores de escala en las fórmulas generales que se encuentran en coordenadas ortogonales.
Aplicaciones
Las aplicaciones clásicas de las coordenadas bipolares están en la resolución de ecuaciones en derivadas parciales, por ejemplo, la ecuación de Laplace o la ecuación de Helmholtz, para las que las coordenadas bipolares permiten una separación de variables. Un ejemplo es el campo eléctrico que rodea dos conductores cilíndricos paralelos con diámetros desiguales.
Los trazadores polares utilizan coordenadas bipolares para describir las rutas necesarias para dibujar una imagen dada.
Extensión a 3 dimensiones
Las coordenadas bipolares forman la base de varios conjuntos de coordenadas ortogonales tridimensionales:
- Las coordenadas bipolares cilíndricas, añadiendo a las coordenadas bipolares en el eje z perpendicular al plano xy.
- Las coordenadas biesféricas, girando las coordenadas bipolares alrededor del eje x, es decir, del eje que conecta los focos.
- Las coordenadas toroidales, girando las coordenadas bipolares alrededor del eje y, es decir, del eje que separa los focos.
Referencias
- «Eric W. Weisstein, Concise Encyclopedia of Mathematics CD-ROM, Bipolar Coordinates, CD-ROM edition 1.0, May 20, 1999». Archivado desde el original el 12 de diciembre de 2007. Consultado el 2 de abril de 2019.
- Polyanin, Andrei Dmitrievich (2002). Handbook of linear partial differential equations for engineers and scientists. CRC Press. p. 476. ISBN 1-58488-299-9.
- Happel, John; Brenner, Howard (1983). Low Reynolds number hydrodynamics: with special applications to particulate media. Mechanics of fluids and transport processes 1. Springer. p. 497. ISBN 978-90-247-2877-0.
Bibliografía
- H. Bateman "Spheroidal and bipolar coordinates", Duke Mathematical Journal 4 (1938), no. 1, 39–50
- Hazewinkel, Michiel, ed. (2001), «Bipolar coordinates», Encyclopaedia of Mathematics (en inglés), Springer, ISBN 978-1556080104.
- Lockwood, E. H. "Bipolar Coordinates." Chapter 25 in A Book of Curves. Cambridge, England: Cambridge University Press, pp. 186–190, 1967.
- Korn GA and Korn TM. (1961) Mathematical Handbook for Scientists and Engineers, McGraw-Hill.