Diagrama ternario
Un diagrama ternario, también denominado triángulo de composición o gráfico ternario o triangular, es un diagrama baricéntrico que se emplea para representar tres variables que suman un valor constante dado. La representación de los valores de las tres variables figura como las posiciones en el interior de un triángulo equilátero, y los tres lados representan las métricas de sus valores. Se utiliza fundamentalmente en campos de la fisicoquímica en el que se permite ver al mismo tiempo la influencia de tres elementos en una disolución,[1] así como en petrología,[2] mineralogía, metalurgia y otras ciencias físicas en los que sea necesario mostrar la composición de sistemas compuestos de tres especies diferentes. Suele tener representación en otros dominios de la ciencia, de esta forma se encuentran en genética de poblaciones donde se suele denominar diagrama de De Finetti, mientras que en teoría de juegos suele recibir el nombre de diagrama simplex.
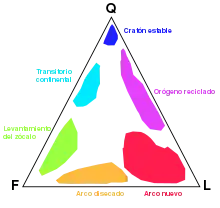
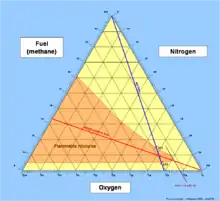
En un diagrama ternario cualquiera, la suma de las proporciones de las variables implicadas a, b y c es siempre igual a una constante K. Los valores suelen ser indicados de forma porcentual y la constante se suele representar en este caso como 1,0 o 100%. Como la suma de las tres proporciones suma siempre K, se puede ver que existe una relación de dependencia entre dos cualesquiera de las variables con la tercera, por ejemplo, se puede representar la variable c como K-a-b. De esta forma sólo se requiere de dos coordenadas (grados de libertad) para encontrar el punto correspondiente a una muestra, es decir, se pueden representar las tres variables en un gráfico bidimensional.
Lectura de datos
Una de las ventajas del uso de un diagrama ternario es precisamente su representación bidimensional. Precisamente pueden establecerse áreas con agrupaciones de puntos con las mismas propiedades: como por ejemplo diagramas de fase.[1] Un diagrama ternario se representa como un triángulo equilátero (Figura 1). Cada punto en el interior de este triángulo representa unívocamente una composición dada de los tres componentes en un sistema de coordenadas. En los vértices se ubican cada uno de los tres componentes. De tal forma que cada vértice supone ser una concentración pura del mismo (100%), y nula de los demás otros dos compuestos. En cambio, cada uno de los lados del triángulo representa una proporción del 0% del compuesto ubicado en su vértice opuesto. A medida que aumenta la proporción de una variable dada en una muestra, el punto se mueve desde la base correspondiente a esa variable hasta el vértice opuesto.
El porcentaje de una especie dada decrece linealmente en este diagrama a medida que se incrementa la distancia respecto a su vértice. En el vértice será de 100% y cuando el punto toque el lado opuesto se considera que la especie ha decrecido en porcentaje hasta anularse. Esto permite representar su proporción mediante rectas paralelas a la base (Figura 2), rectas que van aumentando su valor a medida que se alejan del vértice. La base supone ser un porcentaje nulo del compuesto, a medida que se acerca al vértice la composición crece linealmente. Esta suposición se puede hacer con el resto de los componentes (Figuras 3 y 4) hasta tener una métrica en el interior del triángulo que facilita la medida de los valores.
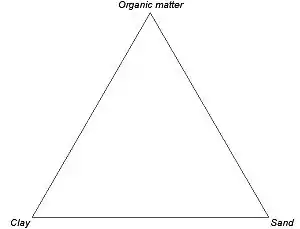 Figura 1 - Ejemplo de diagrama ternario en el que se representan los tres compuestos.
Figura 1 - Ejemplo de diagrama ternario en el que se representan los tres compuestos.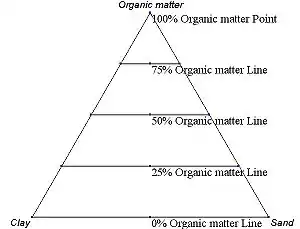 Figura 2 - Diagrama ternario que muestra incrementos a lo largo del primer eje.
Figura 2 - Diagrama ternario que muestra incrementos a lo largo del primer eje.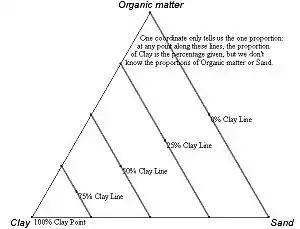 Figura 3 - Diagrama ternario que muestra incrementos a lo largo del segundo eje.
Figura 3 - Diagrama ternario que muestra incrementos a lo largo del segundo eje. Figura 4 - Diagrama ternario que muestra incrementos a lo largo del tercer eje.
Figura 4 - Diagrama ternario que muestra incrementos a lo largo del tercer eje. Figura 5- Diagrama vacío.
Figura 5- Diagrama vacío..png.webp) Diagrama vacío (eje alternativo).
Diagrama vacío (eje alternativo).
Con coordenadas cartesianas
Las coordenadas cartesianas son útiles para representar puntos en el triángulo. Considérese un diagrama en forma de triángulo equilátero donde se sitúa en y en . Entonces está en y la terna está en .
Ejemplo
Este ejemplo muestra cómo funciona este tipo de diagrama para un conjunto hipotético de tres muestras de suelo:
| N.º de muestra | Materia orgánica | Arcilla | Arena | Notas |
| Muestra 1 | 80% | 10% | 10% | Como la proporción de materia orgánica y arcilla suma el 90%, la proporción de arena debe ser del 10%. |
| Muestra 2 | 50% | 40% | 10% | La proporción de arena también es del 10%, pero las proporciones de materia orgánica y arcilla difieren de las dadas en la muestra anterior. |
| Muestra 3 | 10% | 40% | 50% | Esta muestra tiene la misma proporción de arcilla que la muestra 2, pero como tiene una proporción menor de materia orgánica, su proporción de arena tiene que ser mayor pues la suma de todas las proporciones es 100%. |
Representación
 Hallando la primera intersección para representar un punto
Hallando la primera intersección para representar un punto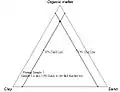 Hallando la segunda intersección para representar un punto
Hallando la segunda intersección para representar un punto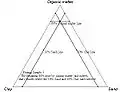 Para representar un punto, no hace falta buscar la tercera intersección, pues depende matemáticamente de las otras dos.
Para representar un punto, no hace falta buscar la tercera intersección, pues depende matemáticamente de las otras dos. Puntos y rectas de intersección
Puntos y rectas de intersección Puntos
Puntos
Referencias
- Luis A Cisternas, (2009), Diagramas de fases y su aplicación, Editorial Reverté, Barcelona
- Myron G. Best - 2009 - Igneous and Metamorphic Petrology - Página 108
Referencias Externas
 Wikimedia Commons alberga una categoría multimedia sobre Diagrama ternario.
Wikimedia Commons alberga una categoría multimedia sobre Diagrama ternario.