Transición de fase

En química, termodinámica y otros campos relacionados, las transiciones de fase (o cambios de fase) son los procesos físicos de transición entre un estado de un medio, identificado por unos parámetros, y otro, con diferentes valores de los parámetros. El término transición de fase se usa más comúnmente para describir transiciones entre estados sólido, líquido y gaseoso de la materia, así como plasma en casos raros.

Este diagrama muestra la nomenclatura para las diferentes transiciones de fase.

Por ejemplo, una fase de un sistema termodinámico y los estados de la materia tienen propiedades físicas uniformes. Durante una transición de fase de un medio dado, ciertas propiedades del medio cambian, a menudo de manera discontinua, como resultado del cambio de alguna condición externa, como la temperatura, la presión u otras. A modo de ejemplo, un líquido puede convertirse en gas al calentarse hasta el punto de ebullición, lo que resulta en un cambio abrupto en el volumen. La medición de las condiciones externas en las que se produce la transformación se denomina transición de fase. Las transiciones de fase comúnmente ocurren en la naturaleza y se usan hoy en día en muchas tecnologías.

Tipos de transición de fase

Los ejemplos de transiciones de fase incluyen:

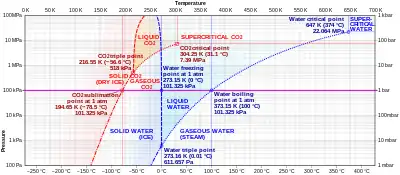
  • Las transiciones entre el sólido, líquido, y fases gaseosas de un componente solo, debido a los efectos de temperatura y/o presión:
Transiciones de fase de la materia
a
Sólido Líquido Gas Plasma
De Sólido Fusión Sublimación
Líquido Solidificación Vaporización
Gas Deposición Condensación Ionización
Plasma Recombinación
Véanse también: Presión de vapor y Diagrama de fase.
Un esquema de fase típico. La línea de puntos da el comportamiento anómalo de agua.
Una pequeña porción de argón sólido de fusión rápida muestra simultáneamente las transiciones de sólido a líquido y de líquido a gas.
Comparación de diagramas de fase de dióxido de carbono (rojo) y agua (azul) que explican sus diferentes transiciones de fase a 1 atmósfera
  • Una transformación eutéctica, en la que un líquido monofásico de dos componentes se enfría y se transforma en dos fases sólidas. El mismo proceso, pero que comienza con un sólido en lugar de un líquido, se denomina transformación eutectoide.
  • Una transformación peritectica, en la cual un sólido monofásico de dos componentes se calienta y se transforma en una fase sólida y una fase líquida.
  • Una descomposición espinodal, en la que una sola fase se enfría y se separa en dos composiciones diferentes de esa misma fase.
  • Transición a una mesofase entre sólido y líquido, como una de las fases de "cristal líquido".
  • La transición entre las fases ferromagnética y paramagnética de los materiales magnéticos en el punto de Curie.
  • La transición entre estructuras magnéticas, ordenadas, proporcionadas o no coordinadas de manera diferente, como en el antimonio de cerio.
  • La transformación martensítica que se presenta como una de las muchas transformaciones de fase en el acero al carbono y se erige como un modelo para las transformaciones de fase de desplazamiento.
  • Cambios en la estructura cristalográfica, como entre ferrita y austenita de hierro.
  • Transiciones de orden-desorden como los aluminuros de alfa-titanio.
  • La dependencia de la geometría de adsorción de la cobertura y la temperatura, como para el hidrógeno sobre el hierro (110).
  • La aparición de superconductividad en ciertos metales y cerámicas cuando se enfría por debajo de una temperatura crítica.
  • La transición entre diferentes estructuras moleculares (polimorfos, alótropos o poliamorfos), especialmente de sólidos, como entre una estructura amorfa y una estructura cristalina, entre dos estructuras cristalinas diferentes o entre dos estructuras amorfas.
  • Condensación cuántica de fluidos bosónicos (condensación de Bose-Einstein). La transición superfluida en helio líquido es un ejemplo de esto.
  • La ruptura de simetrías en las leyes de la física durante la historia temprana del universo a medida que su temperatura se enfría.
  • El fraccionamiento de isótopos ocurre durante una transición de fase, la proporción de isótopos ligeros a pesados en las moléculas involucradas cambia. Cuando el vapor de agua se condensa (un fraccionamiento de equilibrio), los isótopos de agua más pesados (18O y 2H) se enriquecen en la fase líquida, mientras que los isótopos más ligeros (16O y 1H) tienden hacia la fase de vapor.[1]

Las transiciones de fase se producen cuando la energía libre termodinámica de un sistema no es analítica para una selección de variables termodinámicas. Esta condición generalmente se deriva de las interacciones de una gran cantidad de partículas en un sistema y no aparece en sistemas que son demasiado pequeños. Es importante tener en cuenta que las transiciones de fase pueden ocurrir y se definen para sistemas no termodinámicos, donde la temperatura no es un parámetro. Los ejemplos incluyen: transiciones de fase cuántica, transiciones de fase dinámicas y transiciones de fase topológicas (estructurales). En estos tipos de sistemas otros parámetros toman el lugar de la temperatura. Por ejemplo, la probabilidad de conexión reemplaza la temperatura de las redes de filtración.

En el punto de transición de fase (por ejemplo, punto de ebullición) las dos fases de una sustancia, líquido y vapor, tienen energías libres idénticas y, por lo tanto, es igualmente probable que existan. Por debajo del punto de ebullición, el líquido es el estado más estable de los dos, mientras que por encima la forma gaseosa es la más estable.

A veces es posible cambiar el estado de un sistema diabáticamente (en lugar de adiabáticamente) de tal manera que se pueda pasar más allá de un punto de transición de fase sin sufrir una transición de fase. El estado resultante es metaestable, es decir, menos estable que la fase en la que se habría producido la transición, pero tampoco inestable. Esto ocurre en el sobrecalentamiento, el sobreenfriamiento y la sobresaturación, por ejemplo.

Clasificaciones

Clasificación de Ehrenfest

Paul Ehrenfest clasificó las transiciones de fase según el comportamiento de la energía libre termodinámica en función de otras variables termodinámicas.[2] Bajo este esquema, las transiciones de fase se marcaron con la derivada más baja de la energía libre que es discontinua en la transición. Las transiciones de fase de primer orden exhiben una discontinuidad en la primera derivada de la energía libre con respecto a alguna variable termodinámica.[3] Las diversas transiciones sólido/líquido/gas se clasifican como transiciones de primer orden porque implican un cambio discontinuo en la densidad, que es la (inversa de la) primera derivada de la energía libre con respecto a la presión. Las transiciones de fase de segundo orden son continuas en la primera derivada (el parámetro de orden, que es la primera derivada de la energía libre con respecto al campo externo, es continua a lo largo de la transición) pero exhibe discontinuidad en una segunda derivada de la energía libre. Estos incluyen la transición de fase ferromagnética en materiales como el hierro, donde la magnetización, que es la primera derivada de la energía libre con respecto a la intensidad del campo magnético aplicado, aumenta continuamente desde cero a medida que la temperatura desciende por debajo de la temperatura de Curie. La susceptibilidad magnética, la segunda derivada de la energía libre con el campo, cambia de manera discontinua. Bajo el esquema de clasificación de Ehrenfest, en principio podría haber transiciones de fase de tercer, cuarto y orden superior.

Aunque es útil, se ha encontrado que la clasificación de Ehrenfest es un método incompleto para clasificar las transiciones de fase, ya que no tiene en cuenta el caso en que un derivado de la energía libre diverge (lo que solo es posible en el límite termodinámico). Por ejemplo, en la transición ferromagnética, la capacidad calorífica diverge hasta el infinito. El mismo fenómeno también se ve en la transición de fase superconductora.

Clasificaciones modernas

En el esquema de clasificación moderno, las transiciones de fase se dividen en dos grandes categorías, denominadas de manera similar a las clases de Ehrenfest:

Las transiciones de fase de primer orden son aquellas que involucran un calor latente. Durante tal transición, un sistema absorbe o libera una cantidad fija (y generalmente grande) de energía por volumen. Durante este proceso, la temperatura del sistema se mantendrá constante a medida que se agregue calor: el sistema se encuentra en un "régimen de fase mixta" en el que algunas partes del sistema han completado la transición y otras no. Ejemplos familiares son la fusión del hielo o la ebullición del agua (el agua no se convierte instantáneamente en vapor, sino que forma una mezcla turbulenta de agua líquida y burbujas de vapor). Imry y Wortis demostraron que el trastorno extinguido puede ampliar una transición de primer orden. Es decir, la transformación se completa en un rango finito de temperaturas, pero sobreviven fenómenos como el sobreenfriamiento y el sobrecalentamiento y se observa una histéresis en los ciclos térmicos.[4][5][6]

Las transiciones de fase de segundo orden también se denominan transiciones de fase continua. Se caracterizan por una susceptibilidad divergente, una longitud de correlación infinita y un decaimiento de la ley de potencias de las correlaciones cercanas a la criticidad. Ejemplos de transiciones de fase de segundo orden son la transición ferromagnética, la transición superconductora (para un Superconductor de tipo I, la transición de fase es de segundo orden en el campo externo cero y para un Superconductor de tipo II la transición de fase es de segundo orden para ambos estados (estado mixto y estado mixto - transiciones de estado superconductor) y la transición superfluida. En contraste con la viscosidad, la expansión térmica y la capacidad térmica de los materiales amorfos muestran un cambio relativamente repentino a la temperatura de transición vítrea que permite una detección precisa utilizando mediciones de Calorimetría diferencial de barrido.[7] Lev Landau dio una teoría fenomenológica de las transiciones de fase de segundo orden.

Aparte de las transiciones de fase simples y aisladas, existen líneas de transición así como puntos multicríticos, al variar parámetros externos como el campo magnético o la composición.

Varias transiciones son conocidas como transiciones de fase de orden infinito. Son continuos pero no rompen simetrías. El ejemplo más famoso es la transición de Kosterlitz-Thouless en el modelo XY bidimensional. Muchas transiciones de fase cuántica, por ejemplo, en gases de electrones bidimensionales, pertenecen a esta clase.

La transición vítrea se observa en muchos polímeros y otros líquidos que pueden subenfriarse muy por debajo del punto de fusión de la fase cristalina. Esto es atípico en varios aspectos. No es una transición entre los estados fundamentales termodinámicos: se cree ampliamente que el estado fundamental verdadero es siempre cristalino. El vidrio es un estado de desorden enfriado, y su entropía, densidad, etc., dependen de la historia térmica. Por lo tanto, la transición vítrea es principalmente un fenómeno dinámico: al enfriar un líquido, los grados internos de libertad se desequilibran sucesivamente. Algunos métodos teóricos predicen una transición de fase subyacente en el límite hipotético de tiempos de relajación infinitamente largos. Ninguna evidencia experimental directa apoya la existencia de estas transiciones.[8][9] Ninguna evidencia experimental directa apoya la existencia de estas transiciones.

Propiedades características

Coexistencia de fase

Se produce una transición de primer orden ampliada por el desorden en un rango finito de temperaturas en las que la fracción de la fase de equilibrio a baja temperatura crece de cero a uno (100%) a medida que la temperatura desciende. Esta variación continua de las fracciones coexistentes con la temperatura genera interesantes posibilidades. Al enfriarse, algunos líquidos se vitrifican en un vidrio en lugar de transformarse a la fase cristalina de equilibrio. Esto sucede si la velocidad de enfriamiento es más rápida que una velocidad de enfriamiento crítica, y se atribuye a que los movimientos moleculares se vuelven tan lentos que las moléculas no pueden reorganizarse en las posiciones del cristal. .[10] Esta desaceleración ocurre por debajo de una temperatura de formación de vidrio Tg, que puede depender de la presión aplicada.[11] Si la transición de congelación de primer orden se produce en un rango de temperaturas y la Tg cae dentro de este rango, existe una posibilidad interesante de que la transición se detenga cuando es parcial e incompleta. Extender estas ideas a transiciones magnéticas de primer orden detenidas a bajas temperaturas, dio como resultado la observación de transiciones magnéticas incompletas, con dos fases magnéticas coexistiendo, hasta la temperatura más baja. Primero reportado en el caso de una transición ferromagnética a antitransromagnética, tal coexistencia de fase persistente ahora se ha reportado a través de una variedad de transiciones magnéticas de primer orden.[12] Estos incluyen materiales de manganita de magnetorresistencia colosal, materiales magnetocalóricos, materiales de memoria de forma magnética y otros materiales.[13][14][15][16][17] La característica interesante de estas observaciones de la Tg que cae dentro del rango de temperatura en el que se produce la transición es que la transición magnética de primer orden está influenciada por el campo magnético, al igual que la transición estructural está influenciada por la presión. La relativa facilidad con la que se pueden controlar los campos magnéticos, en contraste con la presión, plantea la posibilidad de que uno pueda estudiar la interacción entre Tg y Tc de una manera exhaustiva. La coexistencia de fase a través de transiciones magnéticas de primer orden permitirá la resolución de problemas sobresalientes en la comprensión de los vidrios.

Puntos críticos

En cualquier sistema que contenga fases líquidas y gaseosas, existe una combinación especial de presión y temperatura, conocida como el punto crítico, en la cual la transición entre líquido y gas se convierte en una transición de segundo orden. Cerca del punto crítico, el fluido está lo suficientemente caliente y comprimido como para que la distinción entre las fases líquida y gaseosa sea casi inexistente. Esto se asocia con el fenómeno de la opalescencia crítica, un aspecto lechoso del líquido debido a las fluctuaciones de densidad en todas las longitudes de onda posibles (incluidas las de luz visible).

Simetría

Las transiciones de fase a menudo implican un proceso de simetría rota. Por ejemplo, el enfriamiento de un fluido en un sólido cristalino rompe la simetría de traslación continua: cada punto en el fluido tiene las mismas propiedades, pero cada punto en un cristal no tiene las mismas propiedades (a menos que los puntos se elijan entre los puntos de la red cristalina). Típicamente, la fase de alta temperatura contiene más simetrías que la fase de baja temperatura debido a la ruptura espontánea de simetría, con la excepción de ciertas simetrías accidentales (por ejemplo, la formación de partículas virtuales pesadas, que solo ocurre a bajas temperaturas).[18]

Parámetros de orden

Un parámetro de orden es una medida del grado de orden a través de los límites en un sistema de transición de fase; normalmente oscila entre cero en una fase (generalmente por encima del punto crítico) y distinto de cero en la otra fase. En el punto crítico, la susceptibilidad de los parámetros de orden generalmente divergirá.[19]

Un ejemplo de un parámetro de orden es la magnetización neta en un sistema ferromagnético que experimenta una transición de fase. Para las transiciones de líquido/gas, el parámetro de orden es la diferencia de las densidades.

Desde una perspectiva teórica, los parámetros de orden surgen de la ruptura de simetría. Cuando esto sucede, es necesario introducir una o más variables adicionales para describir el estado del sistema. Por ejemplo, en la fase ferromagnética, se debe proporcionar la magnetización neta, cuya dirección se eligió espontáneamente cuando el sistema se enfrió por debajo del punto de Curie. Sin embargo, teniendo en cuenta que los parámetros de orden también se pueden definir para transiciones que no rompen la simetría. Algunas transiciones de fase, como la superconductora y la ferromagnética, pueden tener parámetros de orden para más de un grado de libertad. En tales fases, el parámetro de orden puede tomar la forma de un número complejo, un vector o incluso un tensor, cuya magnitud va a cero en la transición de fase.

También existen descripciones duales de transiciones de fase en términos de parámetros de desorden. Estos indican la presencia de excitaciones tipo línea, como líneas de vórtice o defecto topológico.

Relevancia en cosmología

Las transiciones de fase de ruptura de simetría desempeñan un papel importante en la cosmología. Lee Smolin y Benjamin y Jeremy Bernstein han especulado que, en el universo primitivo, el vacío (es decir, los diversos campos cuánticos que llenan el espacio) poseía una gran cantidad de simetrías. A medida que el universo se expandía y se enfriaba, el vacío sufría una serie de transiciones de fase de ruptura de simetría. Por ejemplo, la transición electrodébil rompió la simetría SU(2) × U(1) del campo electrodébil en la simetría U (1) del campo electromagnético actual. Esta transición es importante para comprender la asimetría entre la cantidad de materia y la antimateria en el universo actual (Bariogénesis).

Las transiciones de fase progresivas en un universo en expansión están implicadas en el desarrollo del orden en el universo, como lo ilustra el trabajo de Eric Chaisson.[20] y David Layzer.[21]

Exponentes críticos y clases de universalidad

Las transiciones de fase continua son más fáciles de estudiar que las transiciones de primer orden debido a la ausencia de calor latente, y se ha descubierto que tienen muchas propiedades interesantes. Los fenómenos asociados con las transiciones de fase continuas se denominan fenómenos críticos, debido a su asociación con puntos críticos.

Resulta que las transiciones de fase continuas pueden caracterizarse por parámetros conocidos como exponente crítico. El más importante es quizás el exponente que describe la divergencia de la longitud de la correlación térmica al aproximarse a la transición. Por ejemplo, examinemos el comportamiento de la capacidad de calor cerca de tal transición. Variamos la temperatura T del sistema mientras mantenemos todas las demás variables termodinámicas fijas, y encontramos que la transición se produce a una temperatura crítica Tc. Cuando T está cerca de Tc, la capacidad calorífica C generalmente tiene un comportamiento de ley potencial,

La capacidad calorífica de los materiales amorfos tiene tal comportamiento cerca de la temperatura de transición vítrea, donde el exponente crítico universal α = 0.59 Un comportamiento similar, pero con el exponente ν en lugar de α, se aplica a la longitud de correlación.[22]

El exponente ν es positivo. Esto es diferente con α. Su valor real depende del tipo de transición de fase que estamos considerando.

Se creía que los exponentes críticos son los mismos por encima y por debajo de la temperatura crítica. Ahora se ha demostrado que esto no es necesariamente cierto: cuando una simetría continua se divide explícitamente en una simetría discreta por anisotropías irrelevantes (en el sentido de grupo de normalización), entonces algunos exponentes (como \gamma, el exponente de la susceptibilidad) no son idénticos.[23]

Para −1 <α <0, la capacidad calorífica tiene un "giro" en la temperatura de transición. Este es el comportamiento del helio líquido en la transición lambda de un estado normal al estado superfluido, para el cual los experimentos han encontrado α = -0.013 ± 0.003. Se realizó al menos un experimento en condiciones de gravedad cero de un satélite en órbita para minimizar las diferencias de presión en la muestra.[24] Este valor experimental de α concuerda con las predicciones teóricas basadas en la teoría de perturbación variacional.[25]

Para 0 <α <1, la capacidad calorífica diverge a la temperatura de transición (aunque, como α <1, la entalpía permanece finita). Un ejemplo de tal comportamiento es la transición de fase ferromagnética 3D. En el modelo de Ising tridimensional para imanes uniaxiales, estudios teóricos detallados han dado como resultado el exponente α ∼ +0.110.

Algunos sistemas modelo no obedecen a un comportamiento de ley de poder. Por ejemplo, la teoría del campo medio predice una discontinuidad finita de la capacidad calorífica a la temperatura de transición, y el modelo de Ising bidimensional tiene una divergencia logarítmica. Sin embargo, estos sistemas son casos limitantes y una excepción a la regla. Transiciones de fase reales exhiben comportamiento de ley de potencial.

Se definen varios otros exponentes críticos, β, γ, δ, ν y η, que examinan el comportamiento de la ley de potencial de una cantidad física medible cerca de la transición de fase. Los exponentes están relacionados por relaciones de escala, tales como

Se puede mostrar que solo hay dos exponentes independientes, p. Ej. ν y η.

Es un hecho notable que las transiciones de fase que surgen en diferentes sistemas a menudo poseen el mismo conjunto de exponentes críticos. Este fenómeno se conoce como universalidad. Por ejemplo, se ha encontrado que los exponentes críticos en el punto crítico líquido-gas son independientes de la composición química del fluido.

Más impresionante, pero comprensiblemente desde arriba, son una coincidencia exacta para los exponentes críticos de la transición de fase ferromagnética en imanes uniaxiales. Se dice que tales sistemas están en la misma clase de universalidad. La universalidad es una predicción de la teoría del grupo de renormalización de las transiciones de fase, que establece que las propiedades termodinámicas de un sistema cerca de una transición de fase dependen solo de un pequeño número de características, como la dimensionalidad y la simetría, y son insensibles a las propiedades microscópicas subyacentes del sistema. De nuevo, la divergencia de la longitud de correlación es el punto esencial.

Ralentización crítica y otros fenómenos

También hay otros fenómenos críticos; Por ejemplo, además de las funciones estáticas también hay una dinámica crítica. Como consecuencia, en una transición de fase se puede observar una desaceleración crítica o una aceleración. Las grandes clases de universalidad estática de una transición de fase continua se dividen en clases de universalidad dinámica más pequeñas. Además de los exponentes críticos, también hay relaciones universales para ciertas funciones estáticas o dinámicas de los campos magnéticos y las diferencias de temperatura del valor crítico

Teoría de percolación

Otro fenómeno que muestra transiciones de fase y exponentes críticos es la percolación. El ejemplo más simple es quizás la percolación en una red cuadrada bidimensional. Los sitios están ocupados aleatoriamente con probabilidad p. Para valores pequeños de p, los sitios ocupados forman solo pequeños grupos. En un cierto umbral, se forma un clúster gigante y tenemos una transición de fase de segundo orden. El comportamiento de P∞ cercano pc es, P∞~(p-pc)β, dónde β es un exponente crítico.

Transiciones de fase en sistemas biológicos

Las transiciones de fase juegan muchos papeles importantes en los sistemas biológicos. Los ejemplos incluyen la formación de la bicapa lipídica, la transición del glóbulo-espira en el proceso de plegamiento de la proteína y la fusión del ADN, las transiciones de cristal líquido en el proceso de la condensación del ADN y la unión cooperativa del ligando al ADN y las proteínas con el carácter de transición de fase.[26]

En las membranas biológicas, las transiciones de fase de gel a líquido cristalino desempeñan un papel fundamental en el funcionamiento fisiológico de las biomembranas. En la fase de gel, debido a la baja fluidez de las cadenas de lípidos, las proteínas de la membrana tienen un movimiento restringido y, por lo tanto, están restringidas en su papel fisiológico. Las plantas dependen fundamentalmente de la fotosíntesis de las membranas tilacoides de los cloroplásticos que están expuestas a temperaturas ambientales frías. Las membranas tilacoides retienen la fluidez innata incluso a temperaturas relativamente bajas debido a su alto contenido de ácido linolénico, cadena de 18 carbonos con 3 enlaces dobles. La temperatura de transición de fase cristalina de gel a líquido de las membranas biológicas se puede determinar mediante muchas técnicas que incluyen calorimetría, fluorescencia, resonancia paramagnética de electrones de marcaje por rotación y Resonancia magnética nuclear mediante el registro de las mediciones del parámetro correspondiente en una serie de temperaturas de la muestra. También se ha propuesto un método simple para su determinación a partir de intensidades de línea de 13-C RMN.

Se ha propuesto que algunos sistemas biológicos podrían estar cerca de puntos críticos. Los ejemplos incluyen redes neuronales en la salamandra retina, redes de expresión génica de bandadas de aves en Drosophila y plegamiento de proteínas.[27][28][29][30] Sin embargo, no está claro si razones alternativas podrían explicar algunos de los fenómenos que apoyan los argumentos de criticidad.[31] También se ha sugerido que los organismos biológicos comparten dos propiedades clave de las transiciones de fase: el cambio del comportamiento macroscópico y la coherencia de un sistema en un punto crítico.[32]

En grupos de organismos en estrés (cuando se acercan a transiciones críticas), las correlaciones tienden a aumentar, mientras que al mismo tiempo, las fluctuaciones también aumentan. Este efecto es apoyado por muchos experimentos y observaciones de grupos de personas, ratones, árboles y plantas herbáceas.[33]

Véase también

Referencias
  1. Carol Kendall (2004). «Fundamentals of Stable Isotope Geochemistry». USGS. Consultado el 10 de abril de 2014.
  2. Jaeger, Gregg (1 de mayo de 1998). «The Ehrenfest Classification of Phase Transitions: Introduction and Evolution». Archive for History of Exact Sciences 53 (1): 51-81. doi:10.1007/s004070050021.
  3. Blundell, Stephen J.; Katherine M. Blundell (2008). Concepts in Thermal Physics. Oxford University Press. ISBN 978-0-19-856770-7.
  4. Imry, Y.; Wortis, M. (1979). «Influence of quenched impurities on first-order phase transitions». Phys. Rev. B 19 (7): 3580-3585. Bibcode:1979PhRvB..19.3580I. doi:10.1103/physrevb.19.3580.
  5. Kumar, Kranti; Pramanik, A. K.; Banerjee, A.; Chaddah, P.; Roy, S. B.; Park, S.; Zhang, C. L.; Cheong, S.-W. (2006). «Relating supercooling and glass-like arrest of kinetics for phase separated systems: DopedCeFe2and(La,Pr,Ca)MnO3». Physical Review B 73 (18): 184435. Bibcode:2006PhRvB..73r4435K. ISSN 1098-0121. arXiv:cond-mat/0602627. doi:10.1103/PhysRevB.73.184435.
  6. Pasquini, G.; Daroca, D. Pérez; Chiliotte, C.; Lozano, G. S.; Bekeris, V. (2008). «Ordered, Disordered, and Coexistent Stable Vortex Lattices inNbSe2Single Crystals». Physical Review Letters 100 (24): 247003. Bibcode:2008PhRvL.100x7003P. ISSN 0031-9007. PMID 18643617. arXiv:0803.0307. doi:10.1103/PhysRevLett.100.247003.
  7. Ojovan, M.I. (2013). «Ordering and structural changes at the glass-liquid transition». J. Non-Cryst. Solids 382: 79-86. Bibcode:2013JNCS..382...79O. doi:10.1016/j.jnoncrysol.2013.10.016.
  8. Gotze, Wolfgang. "Complex Dynamics of Glass-Forming Liquids: A Mode-Coupling Theory."
  9. Lubchenko, V. Wolynes; Wolynes, Peter G. (2007). «Theory of Structural Glasses and Supercooled Liquids». Annual Review of Physical Chemistry 58: 235-266. Bibcode:2007ARPC...58..235L. PMID 17067282. arXiv:cond-mat/0607349. doi:10.1146/annurev.physchem.58.032806.104653.
  10. Greer, A. L. (1995). «Metallic Glasses». Science 267 (5206): 1947-1953. Bibcode:1995Sci...267.1947G. PMID 17770105. doi:10.1126/science.267.5206.1947.
  11. Tarjus, G. (2007). «Materials science: Metal turned to glass». Nature 448 (7155): 758-759. Bibcode:2007Natur.448..758T. PMID 17700684. doi:10.1038/448758a.
  12. Manekar, M. A.; Chaudhary, S.; Chattopadhyay, M. K.; Singh, K. J.; Roy, S. B.; Chaddah, P. (2001). «First-order transition from antiferromagnetism to ferromagnetism inCe(Fe0.96Al0.04)2». Physical Review B 64 (10): 104416. Bibcode:2001PhRvB..64j4416M. ISSN 0163-1829. arXiv:cond-mat/0012472. doi:10.1103/PhysRevB.64.104416.
  13. Banerjee, A; Pramanik, A K; Kumar, Kranti; Chaddah, P (2006). «Coexisting tunable fractions of glassy and equilibrium long-range-order phases in manganites». Journal of Physics: Condensed Matter 18 (49): L605. Bibcode:2006JPCM...18L.605B. arXiv:cond-mat/0611152. doi:10.1088/0953-8984/18/49/L02.
  14. Wu, Weida; Israel, Casey; Hur, Namjung; Park, Soonyong; Cheong, Sang-Wook; de Lozanne, Alex (2006-11). «Magnetic imaging of a supercooling glass transition in a weakly disordered ferromagnet». Nature Materials (en inglés) 5 (11): 881-886. ISSN 1476-1122. doi:10.1038/nmat1743.
  15. Roy, S. B.; Chattopadhyay, M. K.; Chaddah, P.; Moore, J. D.; Perkins, G. K.; Cohen, L. F.; Gschneidner, K. A.; Pecharsky, V. K. (2006). «Evidence of a magnetic glass state in the magnetocaloric materialGd5Ge4». Physical Review B 74 (1): 012403. Bibcode:2006PhRvB..74a2403R. ISSN 1098-0121. doi:10.1103/PhysRevB.74.012403.
  16. Lakhani, Archana; Banerjee, A; Chaddah, P; Chen, X; Ramanujan, R V (2012). «Magnetic glass in shape memory alloy: Ni45Co5Mn38Sn12». Journal of Physics: Condensed Matter 24 (38): 386004. Bibcode:2012JPCM...24L6004L. ISSN 0953-8984. PMID 22927562. arXiv:1206.2024. doi:10.1088/0953-8984/24/38/386004.
  17. Kushwaha, Pallavi; Lakhani, Archana; Rawat, R.; Chaddah, P. (2009). «Low-temperature study of field-induced antiferromagnetic-ferromagnetic transition in Pd-doped Fe-Rh». Physical Review B 80 (17): 174413. Bibcode:2009PhRvB..80q4413K. ISSN 1098-0121. arXiv:0911.4552. doi:10.1103/PhysRevB.80.174413.
  18. Ivancevic, Vladimir G.; Ivancevic, Tijiana, T. (2008). Complex Nonlinearity. Berlin: Springer. pp. 176-177. ISBN 978-3-540-79357-1. Consultado el 12 de octubre de 2014.
  19. A. D. McNaught and A. Wilkinson, ed. (1997). Compendium of Chemical Terminology. IUPAC. ISBN 978-0-86542-684-9. Consultado el 23 de octubre de 2007.
  20. Chaisson, Cosmic Evolution, Harvard, 2001
  21. David Layzer, Cosmogenesis, The Development of Order in the Universe, Oxford Univ. Press, 1991
  22. Ojovan, Michael I; Lee, William E (2006). «Topologically disordered systems at the glass transition». Journal of Physics: Condensed Matter 18 (50): 11507-11520. Bibcode:2006JPCM...1811507O. doi:10.1088/0953-8984/18/50/007.
  23. Leonard, F.; Delamotte, B. (2015). «Critical exponents can be different on the two sides of a transition». Phys. Rev. Lett. 115 (20): 200601. Bibcode:2015PhRvL.115t0601L. PMID 26613426. arXiv:1508.07852. doi:10.1103/PhysRevLett.115.200601.
  24. Lipa, J.; Nissen, J.; Stricker, D.; Swanson, D.; Chui, T. (2003). «Specific heat of liquid helium in zero gravity very near the lambda point». Physical Review B 68 (17): 174518. Bibcode:2003PhRvB..68q4518L. arXiv:cond-mat/0310163. doi:10.1103/PhysRevB.68.174518.
  25. Kleinert, Hagen (1999). «Critical exponents from seven-loop strong-coupling φ4 theory in three dimensions». Physical Review D 60 (8): 085001. Bibcode:1999PhRvD..60h5001K. arXiv:hep-th/9812197. doi:10.1103/PhysRevD.60.085001.
  26. D.Y. Lando and V.B. Teif (2000). «Long-range interactions between ligands bound to a DNA molecule give rise to adsorption with the character of phase transition of the first kind». J. Biomol. Struct. Dynam. 17 (5): 903-911. PMID 10798534. doi:10.1080/07391102.2000.10506578.
  27. Tkacik, Gasper; Mora, Thierry; Marre, Olivier; Amodei, Dario; Berry II, Michael J.; Bialek, William (2014). «Thermodynamics for a network of neurons: Signatures of criticality». .
  28. Bialek, W; Cavagna, A; Giardina, I (2014). «Social interactions dominate speed control in poising natural flocks near criticality». PNAS 111 (20): 7212-7217. Bibcode:2014PNAS..111.7212B. PMC 4034227. PMID 24785504. arXiv:1307.5563. doi:10.1073/pnas.1324045111.
  29. Krotov, D; Dubuis, J O; Gregor, T; Bialek, W (2014). «Morphogenesis at criticality». PNAS 111 (10): 3683-3688. Bibcode:2014PNAS..111.3683K. PMC 3956198. PMID 24516161. arXiv:1309.2614. doi:10.1073/pnas.1324186111.
  30. Mora, Thierry; Bialek, William (2011). «Are biological systems poised at criticality?». Journal of Statistical Physics 144 (2): 268-302. Bibcode:2011JSP...144..268M. arXiv:1012.2242. doi:10.1007/s10955-011-0229-4.
  31. Schwab, David J; Nemenman, Ilya; Mehta, Pankaj (2014). «Zipf's law and criticality in multivariate data without fine-tuning». Physical Review Letters 113 (6): 068102. Bibcode:2014PhRvL.113f8102S. PMC 5142845. PMID 25148352. arXiv:1310.0448. doi:10.1103/PhysRevLett.113.068102.
  32. Longo, G.; Montévil, M. (1 de agosto de 2011). «From physics to biology by extending criticality and symmetry breakings». Progress in Biophysics and Molecular Biology. Systems Biology and Cancer 106 (2): 340-347. PMID 21419157. arXiv:1103.1833. doi:10.1016/j.pbiomolbio.2011.03.005.
  33. Gorban, A.N.; Smirnova, E.V.; Tyukina, T.A. (August 2010). «Correlations, risk and crisis: From physiology to finance». Physica A: Statistical Mechanics and its Applications 389 (16): 3193-3217. Bibcode:2010PhyA..389.3193G. arXiv:0905.0129. doi:10.1016/j.physa.2010.03.035.

Lectura adicional

ISBN 9971-5-0210-0 9971-5-0210-0 (legible on-line physik.fu-berlin.de)

  • Kleinert, H. Y Verena Schulte-Frohlinde, Propiedades Críticas de φ4-Teorías, Mundiales Científicos (Singapur, 2001); Paperback ISBN 981-02-4659-5

ISBN 981-02-4659-5 981-02-4659-5 (legible on-line aquí).

  • Mussardo G., "Teoría de Campo Estadístico. Una Introducción a Exactamente Solucionó Modelos de Física Estadística", Oxford Prensa Universitaria, 2010.
  • Schroeder, Manfred R., Fractals, caos, leyes de poder : minutos de un paraíso infinito, Nueva York: W. H. Freeman, 1991. Muy libro bien escrito en "semi-estilo" popular—no un textbook—apuntó en una audiencia con alguna formación en matemáticas y las ciencias físicas. Explica lo que scaling en transiciones de fase es todos aproximadamente, entre otras cosas.
  • Yeomans J. M., Mecánica estadística de Transiciones de Fase, Oxford Prensa Universitaria, 1992.
  • H. E. Stanley, Introducción para Realizar por etapas Transiciones y Fenómenos Críticos (Oxford Prensa Universitaria, Oxford y Nueva York 1971).
  • M.R.Khoshbin-e-Khoshnazar, Transición de Fase del Hielo como muestra de transición de fase de sistema finita, (Educación de Física(India)Volumen 32. Núm. 2, Apr - Jun 2016)

Enlaces externos
Este artículo ha sido escrito por Wikipedia. El texto está disponible bajo la licencia Creative Commons - Atribución - CompartirIgual. Pueden aplicarse cláusulas adicionales a los archivos multimedia.