Trapecio isósceles
En geometría euclídea, un trapecio isósceles es un cuadrilátero convexo con un eje de simetría que biseca un par de lados opuestos. Es un caso especial de un trapezoide. Alternativamente, se puede definir como un trapezoide cuyas aristas laterales y sus ángulos con respecto la base son iguales entre sí.[1] Debe señalarse que un paralelogramo sin ángulos rectos no es un trapezoide isósceles debido a la segunda condición, o también porque no tiene ningún eje de simetría. En cualquier trapecio isósceles, dos lados opuestos (las bases) son paralelos, y los otros dos lados tienen igual longitud (propiedades compartidas con los paralelogramos). Las diagonales son también de la misma longitud. Los ángulos de la base de un trapecio isósceles son de la misma medida (de hecho, posee dos pares de ángulos con las bases iguales, siendo el ángulo de una base el ángulo suplementario del ángulo de la otra base).
| Trapecio isósceles | ||
|---|---|---|
 Trapecio isósceles con su eje de simetría | ||
| Características | ||
| Tipo | cuadrilátero, trapecio | |
| Lados | 4 | |
| Vértices | 4 | |
| Grupo de simetría | Dih2, [ ], (*), orden 2 | |
| Polígono dual | Deltoide | |
| Área | ||
| Propiedades | ||
| convexo, cíclico | ||
Casos especiales

Los rectángulos y los cuadrados son normalmente considerados casos especiales de trapecios isósceles, aunque algunos textos no los consideran así.[2]
Otro caso especial es un trapecio isósceles con tres lados de igual longitud, denominado trapecio trilateral[3] o trapecio trisósceles.[4] También pueden ser considerados como particiones de polígonos regulares de 5 lados o más, agrupando 4 vértices consecutivos.
Casos autointersecantes
Cualquier cuadrilátero no autointersecante con un único eje de simetría tiene que ser necesariamente un trapecio isósceles o un deltoide.[5] Sin embargo, si se incluyen los cuadriláteros con cruces, el conjunto de los cuadriláteros simétricos tiene que ser expandido para incluir también los trapecios isósceles cruzados (cuadriláteros en los que los lados cruzados son de igual longitud y los otros dos lados son paralelos), y los antiparalelogramos (cuadriláteros cruzados en los que los lados opuestos tienen igual longitud).
Cada antiparalelogramo tiene un trapezoide isósceles como su envolvente convexa, y puede formarse a partir de las diagonales y lados no paralelos de un trapecio isósceles.[6]
 |
 |
 |
| Convexo | Cruzado | Antiparalelogramo |
|---|
Caracterizaciones
Si se sabe que un cuadrilátero es un trapecio, no basta con comprobar que los lados laterales tienen la misma longitud para asegurar que es un trapecio isósceles, puesto que un rombo es un caso especial de un trapecio con los lados laterales de igual longitud, pero no es un trapecio isósceles debido a que carece de un eje de simetría que pase a través de los puntos medios de dos lados opuestos.
Cualquiera de las propiedades siguientes distingue un trapecio isósceles de otros trapecios:
- Las diagonales tienen la misma longitud.
- Los ángulos de la base tienen la misma medida.
- El segmento que une los puntos medios de los lados paralelos es perpendicular a ellos.
- Los ángulos opuestos son suplementarios, lo que de forma recíproca implica que los trapecios isósceles son cuadriláteros cíclicos.
- Cada diagonal divide a la otra en segmentos con longitudes iguales dos a dos, pero distintas. En términos de la imagen de abajo, AE = DE, BE = CE (y AE ≠ CE, lo que excluiría a los rectángulos).
Si se considera que los rectángulos están incluidos en la clase de los trapecios, entonces se puede definir concisamente un trapecio isósceles como "un cuadrilátero cíclico con diagonales iguales" o como "un cuadrilátero cíclico con un par de lados paralelos" o como "un cuadrilátero convexo con un eje de simetría a través de los puntos medios de dos lados opuestos".[7]
Ángulos
En un trapecio isósceles, los ángulos de las bases deben tener la misma medida dos a dos. En la imagen de abajo, los ángulos ∠ABC y ∠DCB son obtusos y de la misma medida, mientras los ángulos ∠BAD y ∠CDA son agudos y de la misma medida.
Dado que los segmentos AD y BC son paralelos, los ángulos adyacentes a las bases opuestas son suplementarios, es decir, se cumple que ∠ABC + ∠BAD = 180°.
Diagonales y altura
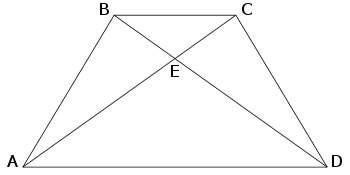
Las diagonales de un trapecio isósceles tienen la misma longitud; esto es, se define como un cuadrilátero equidiagonal. Además, cada una divide a la otra en las mismas proporciones. De acuerdo con la imagen superior, las diagonales AC y BD tienen la misma longitud (AC = BD) y dividen cada una a la otra en segmentos de la misma longitud (AE = DE y BE = CE).
La proporción en qué cada diagonal está dividida es igual a la proporción de las longitudes de los lados paralelos con los que se cruzan, es decir
La longitud de cada diagonal, según el teorema de Ptolomeo, viene dada por
donde a y b son las longitudes de los lados paralelos AD y BC, y c es la longitud de cada arista lateral AB y CD.
La altura, según el teorema de Pitágoras, viene dada por
La distancia del punto E a la base AD está dada por
donde a y b son las longitudes de los lados paralelos AD y BC, y h es la altura del trapecio.
Área
El área de un trapecio isósceles (y de cualquier trapecio) es igual a la media de las longitudes de los lados paralelos (las bases superior e inferior), multiplicada por la altura y dividido entre dos. Tradicionalmente, se expresa como:
- El área de un trapecio es igual a la semisuma de sus bases multiplicada por su altura entre dos
En el esquema adyacente, si se denominan BC = b, AD = a, y BC = b, y la altura h es la longitud del segmento entre AD = a y BC = b perpendicular a ambos, entonces el área K se expresa como sigue:
- , o lo que es lo mismo,
Si en vez de la altura del trapezoide, se conoce la longitud común de las aristas laterales AB = CD = c, entonces el área puede ser calculada utilizando la fórmula de Brahmagupta para el área de un cuadrilátero cíclico, que con dos lados iguales se simplifica a
donde es el semiperímetro del trapecio. Esta fórmula es análoga a la fórmula de Herón para calcular el área de un triángulo. La fórmula anterior para el área también se puede escribir como
Circunradio
El radio del círculo circunscrito está dado por[8]
En un rectángulo, donde a = b, esto se simplifica a .
Véase también
Referencias
- «Copia archivada». Archivado desde el original el 17 de septiembre de 2018. Consultado el 7 de marzo de 2020.
- Larson, Ron; Boswell, Laurie (2016). Big Ideas MATH, Geometry, Texas Edition. Big Ideas Learning, LLC (2016). p. 398. ISBN 978-1608408153.
- Michael de Villiers, Hierarchical Quadrilateral Tree
- isosceles trapezoid
- Halsted, George Bruce (1896), «Chapter XIV. Symmetrical Quadrilaterals», Elementary Synthetic Geometry, J. Wiley & sons, pp. 49-53..
- Whitney, William Dwight; Smith, Benjamin Eli (1911), The Century Dictionary and Cyclopedia, The Century co., p. 1547..
- «Mzone.mweb.co.za». Archivado desde el original el 19 de julio de 2011. Consultado el 7 de marzo de 2020.
- Trapezoid at Math24.net: Formulas and Tables Accessed 1 July 2014.