Trapezoedro
El trapezoedro, antibipirámide o deltoedro n-gonal es el poliedro dual del antiprisma n-gonal.
| Trapezoedros | ||
|---|---|---|
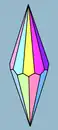 Imagen del sólido | ||
| Caras | 2n Deltoides | |
| Aristas | 4n | |
| Vértices | 2n + 2 | |
| Grupo de simetría | Dnd | |
| Poliedro dual | Antiprisma | |
| Propiedades | ||
| Poliedro convexo, poliedro de caras uniformes | ||
Nombre
Estas figuras, a veces llamados deltoedros, no deben confundirse con deltaedros, cuyas caras son triángulos equiláteros
En los textos que describen los Hábito cristalinos de los minerales, la palabra trapezoedro se utiliza a menudo para el poliedro conocido como Icositetraedro deltoidal.
Formas



- Trapezoedro triangular – 6 caras – dual: octaedro
- Trapezoedro cuadrangular – 8 caras – dual: antiprisma cuadrangular
- Trapezoedro pentagonal – 10 caras – dual: antiprisma pentagonal
- Trapezoedro hexagonal – 12 caras – dual: antiprisma hexagonal
- Trapezoedro heptagonal – 14 caras – dual: antiprisma heptagonal
- Trapezoedro octogonal – 16 caras – dual: antiprisma octogonal
- Trapezoedro eneagonal – 18 caras – dual: antiprisma eneagonal
- Trapezoedro decagonal – 20 caras – dual: antiprisma decagonal
- Fórmula general: Trapezoedro n-gonal – 2n caras – dual: antiprisma n-gonal
Ejemplos
- El Sistema cristalino de los átomos puede repetirse en el espacio usando células Trapezoedrales.
Véase también
 Portal:Matemática. Contenido relacionado con Matemática.
Portal:Matemática. Contenido relacionado con Matemática. Portal:Geometría. Contenido relacionado con Geometría.
Portal:Geometría. Contenido relacionado con Geometría.
Este artículo ha sido escrito por Wikipedia. El texto está disponible bajo la licencia Creative Commons - Atribución - CompartirIgual. Pueden aplicarse cláusulas adicionales a los archivos multimedia.