Variedad algebraica

Para un campo algebraicamente cerrado K y un número natural n, sea Aⁿ un espacio afín n en K, identificado como ${\displaystyle K^{n}}$ mediante la elección de un sistema coordenado afín. Los polinomios  f  en el anillo K[x₁, ..., x_n] se pueden considerar como funciones con valores K en Aⁿ si se evalúa  f  en los puntos en Aⁿ,o sea eligiendo valores en K para cada x_i. Para cada conjunto S de polinómios en K[x₁, ..., x_n], define el lugar geométrico de los ceros Z(S) que son el conjunto de puntos en Aⁿ en los cuales las funciones en S desaparecen simultáneamente, o sea

${\displaystyle Z(S)=\left\{x\in \mathbf {A} ^{n}\mid f(x)=0{\text{ para todo }}f\in S\right\}.}$

Un subconjunto V de Aⁿ es denominado un conjunto algebraico afín si V = Z(S) para algún S.[1]^: 2 Un conjunto algebraico afín no vacío V se denomina irreducible si no puede ser expresado como la unión de dos subconjuntos algebraicos proper.[1]^: 3 Un conjunto algebraico afín irreducibletambién es llamado una variedad afín.[1]^: 3 Muchos autores usan la frase variedad afín para referirse a todo conjunto algebraico afín, irreducible o no[note 1]

A las variedades afines se les puede dar una topología natural declarando que los conjuntos cerrados son precisamente los conjuntos algebraicos afines. Esta topología se denomina topología de Zariski.[1]^: 2

Dado un subconjunto V de Aⁿ, se define I(V) como el ideal de todas las funciones polinómicas que se anulan en V:

${\displaystyle I(V)=\left\{f\in K[x_{1},\ldots ,x_{n}]\mid f(x)=0{\text{ para todo }}x\in V\right\}.}$

Para cualquier conjunto algebraico afín V, el anillo coordenado o anillo estructura de V es el cociente del anilo polinómico por este ideal.[1]^: 4

Sea k un campo cerrado algebraico y sea Pⁿ el espacio proyectivo -n en k. Sea  f  en k[x₀, ..., x_n] un polinomio homogéneo de grado d. No está bien definido para evaluar  f  en puntos de Pⁿ en coordenadas homogéneas. Sin embargo, ya que  f  es homogéneo, lo que significa que  f  (λx₀, ..., λx_n) = λ^d f  (x₀, ..., x_n), tiene sentido preguntarse si  f  desaparece en un punto [x₀ : ... : x_n]. Para cada conjunto S de polinomios homogéneos, definimos el foco cero de S como el conjunto de puntos en Pⁿ en el cual las funciones en S desaparecen:

${\displaystyle Z(S)=\{x\in \mathbf {P} ^{n}\mid f(x)=0{\text{ for all }}f\in S\}.}$

Un subconjunto V de Pⁿ de denomina conjunto algebraico proyectivo si V = Z(S) para algún S.[1]^: 9 Un conjunto algebraico proyectivo irreducible se llama "variedad proyectiva".[1]^: 10

Las variedades proyectivas también cuentan con la topología de Zariski declarando que todos los conjuntos algebraicos son cerrados.

Dado un subconjunto V de Pⁿ, sea I(V) el ideal generado por todos los polinomios homogéneos que desaparecen en V. Para cualquier conjunto algebraico proyectivo V, el anillo de coordenadas de V es el cociente del anillo de polinomios por este ideal.[1]^: 10

Una variedad cuasi-proyectiva es un subconjunto abierto de Zariski de una variedad proyectiva. Obsérvese que toda variedad afín es cuasi-proyectiva.[2] Obsérvese también que el complemento de un conjunto algebraico en una variedad afín es una variedad cuasi-proyectiva; en el contexto de las variedades afines, tal variedad cuasi-proyectiva no suele llamarse variedad sino conjunto construible.

En la geometría algebraica clásica, todas las variedades eran por definición variedades cuasiproyectivas, lo que significa que eran subvariedades abiertas de subvariedades cerradas del espacio proyectivo. Por ejemplo, en el capítulo 1 de Hartshorne, una variedad sobre un campo algebraicamente cerrado se define como una variedad cuasiproyectiva,[1]^: 15 pero a partir del capítulo 2, el término variedad (también llamado variedad abstracta) se refiere a un objeto más general, que localmente es una variedad cuasiproyectiva, pero cuando se ve como un todo no es necesariamente cuasiproyectiva; es decir, podría no tener una incrustación en el espacio proyectivo. Es decir, podría no tener una incrustación en espacio proyectivo.[1]^: 105 Así, clásicamente, la definición de una variedad algebraica requería una incrustación en el espacio proyectivo, y esta incrustación se utilizaba para definir la topología de la variedad y las funciones regulares de la variedad. La desventaja de esta definición es que no todas las variedades tienen incrustaciones naturales en el espacio proyectivo. Por ejemplo, bajo esta definición, el producto P¹ × P¹ no es una variedad hasta que se incrusta en el espacio proyectivo; esto se hace generalmente por la incrustación de Segre. Sin embargo, cualquier variedad que admita una incrustación en el espacio proyectivo admite muchas otras al componer la incrustación con la superficie de Veronese. En consecuencia, muchas nociones que deberían ser intrínsecas, como el concepto de función regular, no lo son obviamente.

El primer intento con éxito de definir una variedad algebraica de forma abstracta, sin una incrustación, fue realizado por André Weil. En su Fundamentos de Geometría Algebraica, Weil definió una variedad algebraica abstracta usando valoraciones. Claude Chevalley hizo una definición de esquema, que servía para un propósito similar, pero era más general. Sin embargo, la definición de esquema de Alexander Grothendieck es aún más general y ha recibido la mayor aceptación. En el lenguaje de Grothendieck, una variedad algebraica abstracta suele definirse como una integral, de esquema separado y de tipo finito sobre un campo algebraicamente cerrado,[1]^{: 104–105} aunque algunos autores abandonan la irreducibilidad o la condición de reducción o de separatividad o permiten que el campo subyacente no sea algebraicamente cerrado.[note 2] Las variedades algebraicas clásicas son la integral cuasiproyectiva separada de esquemas de tipo finito sobre un campo algebraicamente cerrado.

Uno de los primeros ejemplos de una variedades algebraicas no-cuasiproyectiva fue provisto formulado por Nagata.[3] El ejemplo de Nagat no era completo (el análogo de compacticidad), pero poco después Nagata encontró una superficie algebraica que era completa y no-proyectiva.[4][1] Desde entonces se han encontrado otros ejemplos; por ejemplo, es sencillo construir una variedad tórica que no es cuasi-proyectiva pero sí completa.[5]

Sea k = C, y A² sea el espacio afín bidimensional sobre C. Los polinomios en el anillo C[x, y] pueden verse como funciones de valor complejo en A² evaluando en los puntos de A². Sea el subconjunto S de C[x, y] un único elemento  f  (x, y):

${\displaystyle f(x,y)=x+y-1.}$

El lugar cero de  f  (x, y) es el conjunto de puntos de A² en los que esta función desaparece: es el conjunto de todos los pares de números complejos (x, y) tales que y = 1 - x. Esto se llama una línea en el plano afín. En la topología clásica, procedente de la topología sobre los números complejos, una recta compleja es un colector real de dimensión dos. Se trata del conjunto Z( f ):

${\displaystyle Z(f)=\{(x,1-x)\in \mathbf {C} ^{2}\}.}$

Así, el subconjunto V = Z( f ) de A² es un conjunto algebraico. El conjunto V no es vacío. Es irreducible, ya que no puede escribirse como la unión de dos subconjuntos algebraicos propios. Por lo tanto, es una variedad algebraica afín.

Sea k = C, y A² sea el espacio afín bidimensional sobre C. Los polinomios en el anillo C[x, y] pueden verse como funciones de valor complejo en A² evaluando en los puntos de A². Sea el subconjunto S de C[x, y] el que contenga un único elemento g(x, y):

${\displaystyle g(x,y)=x^{2}+y^{2}-1.}$

El lóbulo cero de g(x, y) es el conjunto de puntos de A² en los que esta función desaparece, es decir, el conjunto de puntos (x, y) tales que x² + y² = 1. Como g(x, y) es un polinomio absolutamente irreducible, se trata de una variedad algebraica. El conjunto de sus puntos reales (es decir, los puntos para los que x e y son números reales), se conoce como el círculo unitario; este nombre también se da a menudo a toda la variedad.

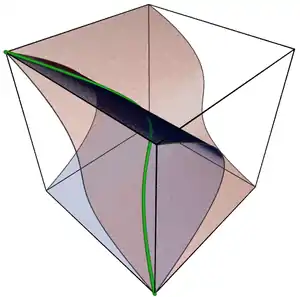
El siguiente ejemplo no es ni una hipersuperficie, ni un espacio lineal, ni un único punto. Sea A'³ el espacio afín tridimensional sobre C'. El conjunto de puntos (x, x ², x ³) para x en C es una variedad algebraica, y más precisamente una curva algebraica que no está contenida en ningún plano.[note 3] Es la cúbica alabeada que se muestra en la figura anterior. Se puede definir mediante las ecuaciones

${\displaystyle {\begin{aligned}y-x^{2}&=0\\z-x^{3}&=0\end{aligned}}}$

La irreducibilidad de este conjunto algebraico necesita una demostración. Una aproximación en este caso es comprobar que la proyección (x, y, z) → (x, y) es inyectiva sobre el conjunto de las soluciones y que su imagen es una curva plana irreducible.

Para ejemplos más difíciles, siempre se puede dar una prueba similar, pero puede implicar un cálculo difícil: primero una base de Gröbner para calcular la dimensión, seguida de un cambio lineal aleatorio de variables (no siempre necesario); luego una base de Gröbner para otro orden monomial para calcular la proyección y probar que es genéricamente inyectiva y que su imagen es una hipersuperficie, y finalmente una factorización polinómica para probar la irreductibilidad de la imagen.